Урок по алгебре в 9 классе по теме: «Четная и нечетная функции»
 Скачать 62.21 Kb.
|
| Открытый урок по алгебре в 9 классе по теме: « Четная и нечетная функции» Учебник и задачник А.Г. Мордкович Алгебра 9 класс. Урок подготовила и провела Железнова Я.А. Цели: формирование понятий: « симметричное множество», « четная функция», «нечетная функция», научить исследовать функцию на четность, определять по графику четность и нечетность функции, научит строить четные и нечетные функции, проверка усвоения новых знаний умений и навыков. А также развитие общеучебных навыков: устной и письменной речи, умения задавать вопросы, слушать других, понимать и оценивать, развитие познавательных процессов (внимание, восприятие, памяти, представления и воображения). Оборудование: кодоскоп, распечатанные пленки для него: определение симметричного множества, решение примера 4, четная и нечетная функция, графики и система координат. На каждого ученика карточка с алгоритмом и для самостоятельной работы. Структура урока: 1. Орг. момент. 2.. Подготовка к изучению нового материала и постановка цели урока
Так как в этот день в классе два урока алгебры , то домашнее задание будет дано на втором уроке Тип урока: изучение и закрепление нового материала Так как в этот день в классе два урока алгебры , то домашнее задание будет дано на втором уроке 1. Орг. момент. Приветствие класса, проверка присутствующих в классе. 2. Подготовка к изучению нового материала и постановка цели урока (беседа). ? Что такое область определения функции? ? Как она обозначается? ? Какие элементы называют противоположными: ? Приведите примеры До сегодняшнего дня мы с вами обсуждали только те свойства функции, которые были вам знакомы. Но запас свойств будет пополняться. Сегодня мы с вами рассмотрим еще два свойства. Записываем: число, классная работа тема урока: « Четная и нечетная функции» 3. Изучение нового материала и первичное закрепление А) Для этого нам понадобится новое понятие: «Симметричное множество» Как вы думаете, что это за множество? (Обсуждение). Записываем: Если числовое множество Х вместе с каждым своим элементом х содержит и противоположный элемент – х, то Х называют симметричным множеством. (Это же определение выводится через кодоскоп) Определите симметричное множество или нет: (-2; 2), [ -5; 5], [0;  ), ( ), (-2; 3), [-5; 5).Б) Рассмотрим алгоритм исследование функции на четность. ( каждому ученику раздаются карточки с алгоритмом) Алгоритм исследования функции на четность
  2. Найти f (–x) Функция не является ни четной, ни нечетной  3. Верно ли, что f (x ) = f ( – x)   4. Найти – f (x) Функция четная 5. Верно ли, что – f (x) = f ( – x)  нет Функция нечетная Функция не является ни четной, ни нечетной Разделим тетрадную страницу на 4 колонки и впишем в них 4 примера. ( Работа выполняется строго по пунктам алгоритма: сначала 1 шаг в первом примере, затем 1 шаг во втором примере, 1 шаг в третьем примере, 1 шаг в четвертом, потом второй шаг в 1 примере и.т.д. Первый пример учитель делает, второй – учитель с подсказкой учеников, третий - ученик, четвертый самостоятельно без проверки).
Давайте проверим как вы самостоятельно решили 4 пример ( сверка с готовым решением по кодоскопу). В) Рассмотрим более сложные задания ( ученики у доски) 1) f(x) = x3– 3x + 1 2) f(x) =  3) f(x) =  [–2; 2),4) f(x)=3  –2 x4Г) Теперь обсудим геометрический смысл свойства четности и свойства нечетности функции. П 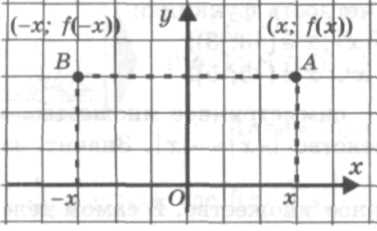 усть у = f(x) — четная функция, т. е. f(-x) = f(x) для любого х  D{f). Рассмотрим две точки графика функции: А(х; f(x)) и В(-х; f(-x)). Так как f(-x) = f(x), то у точек А и В абсциссы являются противоположными числами, а ординаты одинаковы. Эти точки симметричны относительно оси у. Таким образом, для каждой точки А графика четной функции у = f(x) существует симметричная ей относительно оси у точка В того же графика. Это означает, что Записываем : График четной функции симметричен относительно оси ординат. (Это же определение выводится через кодоскоп) Верно и обратное утверждение. Сформулируйте его. Записываем: Если график функции симметричен относительно оси ординат, то функция четная. (Это же определение выводится через кодоскоп) П 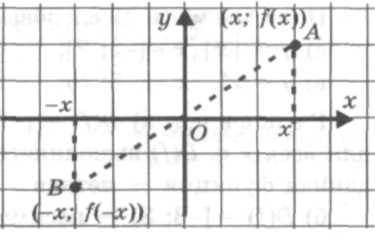 усть у = f(x) — нечетная функция, т. е. f(-x) = -f(x) для любого х D{f). Рассмотрим две точки графика функции: А(х; f(x)) и В(-х; f(-x)). Так как f(-x) = -f(x), то у точек А и В абсциссы являются противоположными числами и ординаты являются противоположными числами. Эти точки симметричны относительно начала координат. Таким образом, для каждой точки А графика нечетной функции у = f(x) существует симметричная ей относительно начала координат точка В того же графика. Это означает, что Записываем : График нечетной функции симметричен относительно начала координат. (Это же определение выводится через кодоскоп) Верно и обратное утверждение. Сформулируйте его Записываем : Если график функции симметричен относительно начала координат, то функция нечетная. (Это же определение выводится через кодоскоп)
4. Итоги 1) Подведем итог: ( фронтальный опрос) ? Какое множество называют симметричным ? С какими новыми свойствами мы свойствами познакомились ? Назовите этапы алгоритма исследования функции на четность ? Продолжите фразы:
2 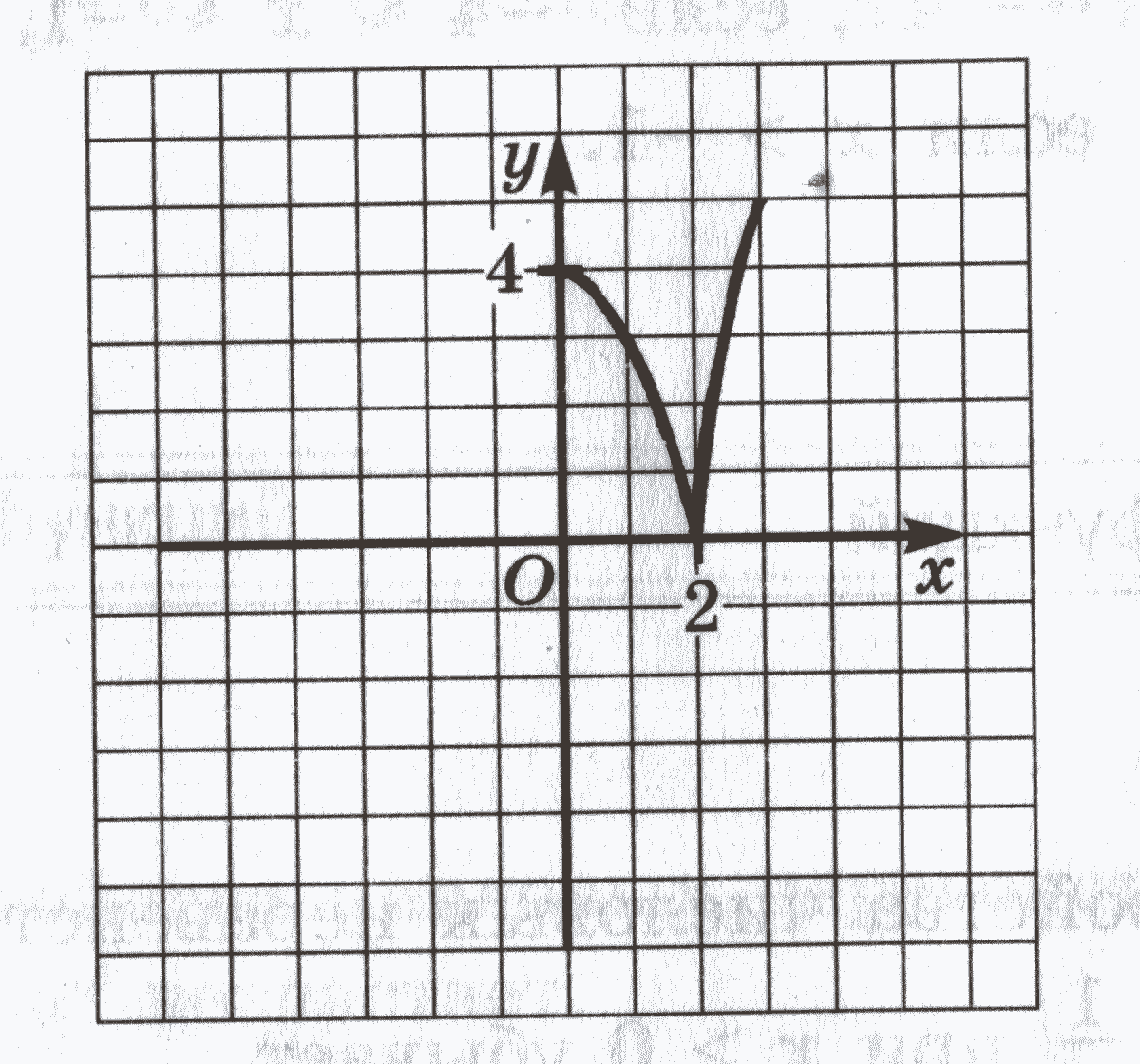 ) Самостоятельная работа по теме: Вариант 1 1. Исследовать на четность функциюy = x ( x4 + 1 ) 2. На рисунке изображена часть графика четной функции. Достройте график этой функции Вариант 2 1 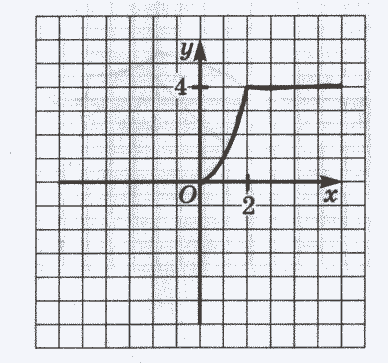 . Исследовать на четность функцию y = x3 –  2. На рисунке изображена часть графика нечетной функции. Достройте график этой функции Самостоятельная работа на карточках по вариантам. Сдается на оценку. |
f(x)