Урок по теме «Действия с натуральными числами» Дайте Ребенку радость умственного труда В. А. Сухомлинский Цель
 Скачать 99.35 Kb. Скачать 99.35 Kb.
|
 Урок математики в 5 «А» классе Урок математики в 5 «А» классе «Мы обретаем ту силу, что преодолели» (обобщающий урок по теме «Действия с натуральными числами») Дайте Ребенку радость умственного труда В.А.Сухомлинский Цель: формирование активной учебно-познавательной деятельности и духовно-нравственных ценностей учащихся. Учебные задачи, направленные на достижение личностных результатов обучения: - помочь учащимся осознать значение, смысл для них изучение данной темы; - создание условий в образовательном процессе, которые способствуют раскрытию и удовлетворению духовно-нравственных ценностей учащихся; - развитие познавательных интересов учащихся. Учебные задачи, направленные на достижение метапредметных результатов обучения: - формирование умений организации учебной деятельности: постановки целей, планирования, самоконтроля, коррекции, оценки результатов, способности к мобилизации сил и энергии для продолжительной умственной деятельности, преодолению трудностей; - формирование умений самостоятельно выделять и формулировать познавательную цель, осознанно и произвольно строить речевое высказывание, рефлексии способов и условий действия; - формирование логических умений: анализу, синтезу, сравнению, обобщению, построению цепочек рассуждений; - формирование интеллектуальной корректности, критичности мышления, вежливых доброжелательных отношений, психологического согласия учащихся с намерениями учителя, основы для творения духовной общности. Учебные задачи, направленные на достижение предметных результатов обучения: - углубление знаний учащихся по теме «Действия с натуральными числами». Оборудование урока: компьютер, мультимедийный проектор. Друзья мои! Сегодня на нашем уроке присутствуют учителя школ города и области. Поприветствуем их. Будем считать, что они у нас в гостях. Я знаю точно, что они любят получать подарки. Что мы можем подарить им? Наш урок. Называется он «Мы обретаем ту силу, что преодолели». Я думаю, им понравится урок, если он доставит вам самим радость, вызовет у вас гордость от того, что вы сумели преодолеть трудности, проявить себя, увидеть красоту математики. Ваш успех будет рождать вдохновение и тогда обязательно появится интерес к математике и вы полюбите ее. Они будут радоваться и удивляться, если увидят это вдохновение и красоту вашей мысли. Помните! Самое ценное в человеке – привычка красиво мыслить. Мысль превыше всего между людьми на Земле. Где твоя мысль , там твоя и высота. У меня нет сомнения, что вы будете стараться и у вас обязательно все получится. Я верю в вас. Если что, я рядом с вами. Помните, ваши высказывания должны выражать мысль, а качество вашего мышления выражать вашу сущность. Пусть лейтмотивом нашего урока буду обращение к учителям Василия Александровича Сухомлинского «Дайте Ребенку Радость умственного труда». Всем нам, я думаю, хотелось бы, чтобы урок стал уроком вежливых, доброжелательных отношений, духовной общности, научил в каждом из нас видеть светлую сторону и вступать в такое общение, которое доставляло нам радость и помогло проявить собственную индивидуальность. Одухотворять наш урок будем заданиями, которые вырабатывают привычку красиво мыслить. Работаем в быстром темпе, на высоком уровне сложности, идя от успеха к успеху, осознавая ход наших умственных действий. С чего начинается урок. Я показываю все задачи, которые есть на экране и предлагаю учащимся внимательно посмотреть и ознакомиться со всеми. Пусть ученики увидят все это богатство и, наверное, удивятся и восхитятся. Познание начинается с удивления! (Аристотель) Давайте согласуем план нашего урока.
3. Сюрприз от Алекса. 4. Чем обогатил нас урок. 5. Подумаем дома. Обращаю ваше внимание на мудрое высказывание Ш.А.Амонашвили: «Мы обретаем ту силу, что преодолели». Друзья мои, как вы понимаете это высказывание? Давайте поразмышляем! После размышления учащихся, предлагаю обраться к записи: Кто ищет трудность, находит Друзья мои! Вообразите себе, что на этом уроке, каждый из вас не ученик, а великий математик: Максим Чикалев, ты – Пифагор, Алекс Шрестха, ты-Архимед, Сережа Курбатов, ты - Чебышев, Влад Карпинский, ты – Карл Гаусс, Максим Хватов, ты – Колмогоров Андрей Николаевич, Гриша Модин, ты – Эварист Галуа. Математика очень вас любит. Вы также очень любите математику. Скажите самому себе. Я математик. Повторите себе это несколько раз. После такого настроя на урок предлагаю учащимся решить задачу №1. Задача №1 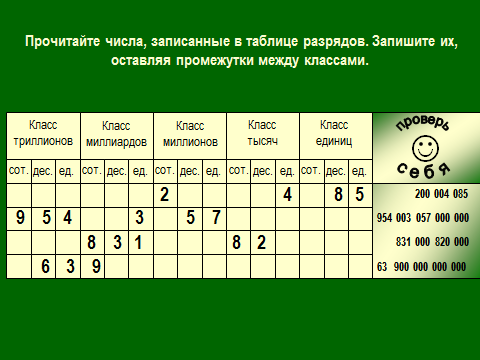 Какое самое большое натуральное число? Натуральный ряд чисел бесконечен, как наша жизнь. Я думаю, все мы верим в реальность бессмертия человеческого духа, понимаем земную жизнь как отрезок пути, духовного совершенствования и восхождения. Задача №2 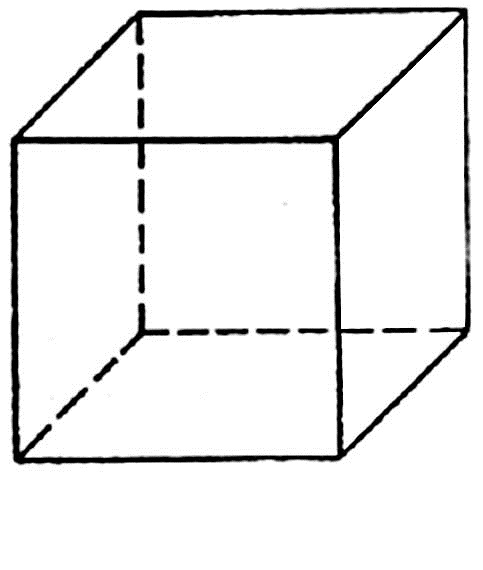 Перед вами куб. Он сделан из плотной бумаги. Вообразим, что этот куб мы раскрываем и из него делаем плоскую геометрическую фигуру. На что эта плоская геометрическая фигура будет похожа. Ответ. Крест  Обратим внимание, что получился крест. Можно получить разные фигуры, но можно получить и крест. Кто-то может сказать, что и у него крестик есть и даже достать его. Как здорово, что у тебя есть такой крест. Задача №3 Как видите, на картинке изображена эмблема олимпиады. Вам нужно расставить в каждой из областей цифры от 1 до 9 так, чтобы никакая цифра не стояла два раза и при этом в каждом кружке сумма цифр была 11. Если у вас получилось это сделать, то какая цифра будет стоять в области с вопросительным знаком?  Ответ: 6. Суть заключается в том, что девять может быть только в крайней области. Значит и восемь может быть только в крайней области. Сответственно, возле них может быть только 2 или 3. Оставшиеся цифры в двух кружочках подставляются так, чтобы получилось одиннадцать. Остается шестерка. Задача №4 Натуральные числа – это числа, используемые для счета. Сосчитайте, сколько квадратов на этом рисунке? 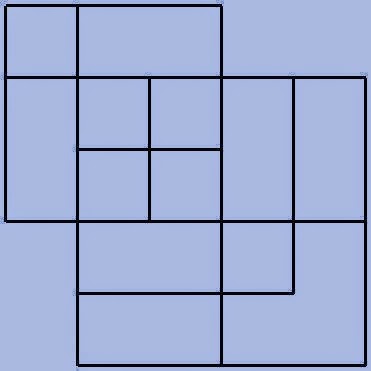 Ответ: 17 квадратов. Если принять сторону самого маленького квадрата за единицу, то на этом рисунке будет: 6 квадратов со стороной 1; 8 квадратов со стороной 2; 2 квадрата со стороной 3; 1 один квадрат со стороной 4 Задача №5 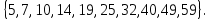 Посмотрите на множество этих чисел (несколько секунд). Запомните этот ряд чисел и порядок расположения чисел. После этого приглашаем к доске 2-3 учащихся. Они стоят спиной к доске, лицом к классу и каждый из них называет этот ряд чисел. Кто правильно называет ряд, тому аплодируем. Если кто-то ошибся, просим садиться и убедиться в своей ошибке. Каждый желающий может продемонстрировать свою память. Посмотрите на множество этих чисел (несколько секунд). Запомните этот ряд чисел и порядок расположения чисел. После этого приглашаем к доске 2-3 учащихся. Они стоят спиной к доске, лицом к классу и каждый из них называет этот ряд чисел. Кто правильно называет ряд, тому аплодируем. Если кто-то ошибся, просим садиться и убедиться в своей ошибке. Каждый желающий может продемонстрировать свою память. Задача №6 Множество состоит из разных фигур. Запомните порядок элементов этого множества. 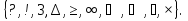  Что изменилось в множестве Что изменилось в множестве 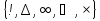 ? ?Ответ. Элементы, стоящие на нечетных местах исчезли из множества. Задача №7 Ответ: 500500. С этой задачей связана история, которую рассказывают об известном немецком математике Карле Гауссе. Когда учитель предложил ученикам третьего класса сложить все числа от 1 до 100 включительно, рассчитывая при этом надолго занять их работой, маленький Карл моментально подошел с готовым ответом: 1+2+3+ …+98+99+100 = 5050. Как он это сделал? Используя найденный способ решения найдите сумму: 1+2+3+…+7+8+9+ 10; 1+2+3+…+98+99+100; 1+2+3+…+998+999+1000; 1+2+3+…+( 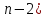 + ( + (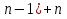 . .Ответ: 55; 5050; 500500; 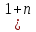 ) · ) ·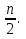 Задача №8 В 1544 г. вышла книга немецкого математика М.Штифеля “Общая арифметика”. Штифель составил таблицу:
Чем замечательна эта таблица. Подумайте, как найти по данной таблице произведение 2 и 64. Представьте себе, что мы не умеем умножать и делить. Но нам понадобилось умножить, например, 2 на 64. В таблице над 2 написано 1, а над 64 написано 6. Сложим эти числа. Получилось 7. Под семеркой читаем 128. Это и есть искомое произведение. Другой пример. Разделим 32 на 8. Поступаем аналогично: 32 –> 5 8 –> 3 5 - 3 = 2 2 –> 4 32 : 8 = 4 Задача №9 Когда шестилетний Колмогоров нашёл, что сумма первых n нечётных чисел равна п2. Как он при этом рассуждал? Как вы думаете? Чему равна сумма 1+3+5+7+9+11+13+15+17+19? Сумма первых 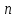 нечетных чисел равна нечетных чисел равна 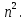 Например, сумма первых 10 нечетных чисел равна 100. Например, сумма первых 10 нечетных чисел равна 100. Ответ. Он вероятно рассуждал так: «Возьмем число 1. Представим это геометрически, как один квадратик. Теперь прибавим к единице число 3. К нашему квадратику прибавим ещё три квадратика. Затем прибавим число 5, добавим ещё 5 квадратиков – 2 сверху, 2 справа и один в углу. Получится квадратик 3 на 3. Девять. Каждый раз мы будем прибавлять к квадрату п на п новый уголок, состоящий из п квадратиков сверху, п квадратиков справа и одного в углу. Вот и будет получаться новый квадрат со стороной п + 1. Значит, прибавляя последовательные нечётные числа, мы всегда будем получать квадрат их количества». Задача №10 Что должно находиться в самом верхнем квадрате?  Ответ: Мысленно закройте правую часть каждого квадрата. Получившиеся числа подчиняются следующей закономерности: число в клетке равно сумме чисел в "основаниях". Т.е. сверху должно быть число 11 
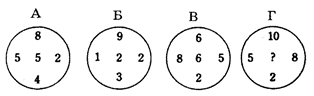 Какое число должно стоять в центре круга Г? Ответ: 2. (10/2)+5-8 =2 Задача №12 Рассмотрим числовую пирамиду 1 ∙ 9+2=11 12 ∙ 9+3=111 123 ∙ 9+4=1111 1234 ∙ 9+5=11111 12345 ∙ 9+6=111111 123456 ∙ 9+7=1111111 1234567 ∙ 9+8=11111111 12345678 ∙ 9+9=111111111 Как она получается? Например: 123 ∙ 9+4= 123 ∙ (10-1)+4= 1230 – 123 + 4= 1234-123 =1111. Рассмотрим: 12345679 ∙ 9 = (12345678 +1) ∙ 9 = 12345678 ∙ 9 + 9 =111111111. Но тогда 12345679 ∙ 9 = 111111111 12345679 ∙ 18 = 222222222 12345679 ∙ 27 = 333333333 12345679 ∙ 36 = 444444444 12345679 ∙ 45 = 555555555 12345679 ∙ 54 = 666666666 12345679 ∙ 63 = 777777777 12345679 ∙ 72 = 888888888 12345679 ∙ 81 =999999999 Принимая во внимание данные пирамиды рассмотрим следующую задачу. Возите любую цифру из верхнего ряда. Умножьте его на 9. Полученное произведение умножьте на верхнее число. Каков будет результат? 12345679  9 9 3 Ответ: 333333333. 3 Ответ: 333333333.________ ????????? Задача №13 Познакомимся с интересными приемами быстрого счета. Вычислим  21 21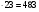 . Это можно сделать устно. Помогите мне, пожалуйста. Прекрасно: . Это можно сделать устно. Помогите мне, пожалуйста. Прекрасно: 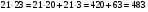 . . Я не сомневаюсь, что каждый из вас сможет перемножить эти числа «столбиком». Можно еще перемножить эти числа методом Ферроля по алгоритму: 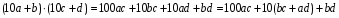 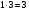 = = 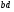 -результат перемножения единиц; -результат перемножения единиц; 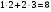 = = 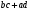 - число десятков в результате (перемножаем средние числа, крайние числа и суммируем); - число десятков в результате (перемножаем средние числа, крайние числа и суммируем);2 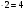 = =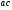 - результат перемножения десятков. - результат перемножения десятков.А теперь посмотрим на схему: 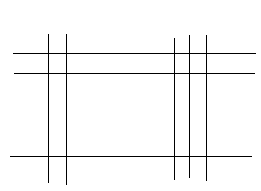 Реализует ли данная схема этот алгоритм. Если да, то каким образом? Две верхние и одна нижняя горизонтальные линии соответствуют числу десятков и единиц первого числа, а две левые и три правые вертикальные линии соответствуют числу десятков и единиц второго числа. Число точек пересечения горизонтальных и вертикальных линий в правом нижнем углу (3) - результат перемножения единиц. Число точек пересечения линий в правом верхнем углу и левом нижнем углу суммарно (6+2=8) - дают число десятков, число точек пересечения в верхнем левом углу (4) – результат перемножения десятков. 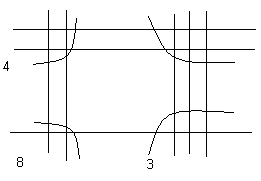 Кто желает попробовать? Пожалуйста: 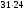 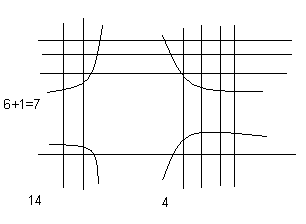 31·24=744. Как приятно с вами работать! Нет сомнения, что все разобрались с этим алгоритмом. Сюрприз от Алекса. - Хотите, я с помощью действий над натуральными числами узнаю дату вашего рождения. Выполните пожалуйста: 1. Порядковый месяц рождения умножьте на 100. 2. К результату прибавьте число месяца рождения. 3. Полученный результат умножьте на 2. 4. К полученному результату прибавьте 8. 5. Полученный результат умножьте на 5. 6. К результату прибавьте 4. 7. Умножьте полученное на 10. 8. К результату прибавьте 4. 9. К полученному результату прибавьте возраст. Сообщите результат вычислений. (От полученного результата отнять 444). Пример. Порядковый номер месяца рождения – 4(апрель). Число месяца рождения – 19. Возраст – 58. Имеем: ((((4×100+19)×2+8) 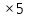 +4)×10+4)+58=42402 +4)×10+4)+58=4240242402-444=41958=4 19 58 (19 апреля 58 лет) Над этим секретом подумайте дома. Домашнее задание. Это для вас и ваших родителей. 1.Набор домино был выложен в прямоугольник, затем числа в костяшках были записаны, а сами костяшки удалены. Требуется восстановить выложенный набор домино, чтобы он соответствовал предоставленным числам. Головоломка имеет единственное решение. 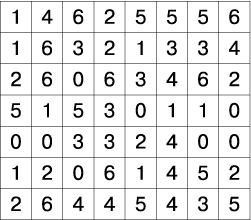 Ответ:  2. Прошу исследовать одно странное число, о котором я вычитал в интернете. Число это: 142857. Умножьте это число на 2,3,4 и т. д. до 9, на 22,33,44 и т. д. до 99 и исследуйте, что произойдет с цифрами, из которых состоит это число. Друзья мои! Наш урок заканчивается. Он назывался «Мы обретаем ту силу, что преодолели». Вы сейчас вернетесь домой. Родители спросят вас, как прошел открытый урок математики. Вообразите себе, что они стоят перед вами, а вы рассказываете им, что было на уроке математики. Что вы скажете им? - Мы способны преодолевать трудности. - Что трудность есть путь к мудрости. - Кто ищет трудность - находит мудрость. - Мы увидели, что математика очень красивая наука. - Стали ли вы сильнее, преодолев трудности при решении задач? - Понравился ли он вам урок и доставил ли он вам радость? - Вызвал ли он у вас гордость от того, что вы сумели преодолеть трудности, проявить себя. - Как оценили вы свои возможности при решении задач? - Приятно ли было вам общаться с учителями и товарищами. Доставило ли оно вам радость. - Трудные, интересные ли были задачи? - Что не понравилось вам на уроке? - Согласны ли вы, что такие задания, если выполнять их регулярно вырабатывают привычку красиво мыслить. - Как вы оцениваете уровень сложности задач, темп урока? - Выполнили ли мы план урока? Все ли получилось так как задумали? Кто желает высказать свое мнение? После высказывания детей, учитель благодарит детей. - Благодарю всех. Вы мне очень помогли провести этот урок. Мне было приятно с вами. |