Операции над комплексными числами в тригонометрической форме записи
 Скачать 23.64 Kb. Скачать 23.64 Kb.
|
| Операции над комплексными числами в тригонометрической форме записи. Геометрически комплексные числа складываются по правилу параллелограмма. Но складывать или вычитать два комплексных числа в тригонометрической форме записи крайне затруднительно. Поэтому данные операции в тригонометрической форме записи мы рассматривать не будем. 1. Умножение. Правило. При перемножении комплексных чисел в тригонометрической форме записи их модули перемножаются, а аргументы складываются. 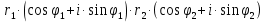 = =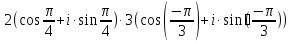 = =2. Деление. Правило. При делении комплексных чисел в тригонометрической форме записи их модули соответственно делятся, а аргументы вычитаются. 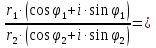 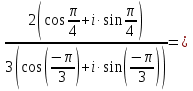 3. Возведение в степень. Правило. При возведении в n-ую степень комплексного числа в тригонометрической форме записи нужно возвести в n-ую степень модуль, а аргумент умножить на число n. 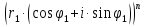 = =формула Муавра. 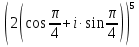 = =4. Извлечение корня. Правило. Чтобы извлечь корень n-ой степени из комплексного числа в тригонометрической форме записи, нужно извлечь корень n-ой степени из модуля этого комплексного числа, а к аргументу прибавить 2πk и полученную сумму разделить на n 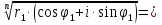 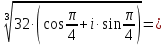 Операции над комплексными числами в тригонометрической форме записи. Геометрически комплексные числа складываются по правилу параллелограмма. Но складывать или вычитать два комплексных числа в тригонометрической форме записи крайне затруднительно. Поэтому данные операции в тригонометрической форме записи мы рассматривать не будем. 1. Умножение. Правило. При перемножении комплексных чисел в тригонометрической форме записи их модули перемножаются, а аргументы складываются. 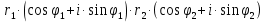 = =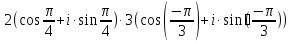 = =2. Деление. Правило. При делении комплексных чисел в тригонометрической форме записи их модули соответственно делятся, а аргументы вычитаются. 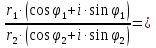 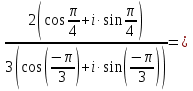 3. Возведение в степень. Правило. При возведении в n-ую степень комплексного числа в тригонометрической форме записи нужно возвести в n-ую степень модуль, а аргумент умножить на число n. 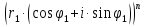 = =формула Муавра. 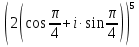 = =4. Извлечение корня. Правило. Чтобы извлечь корень n-ой степени из комплексного числа в тригонометрической форме записи, нужно извлечь корень n-ой степени из модуля этого комплексного числа, а к аргументу прибавить 2πk и полученную сумму разделить на n 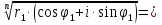 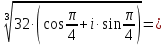 |