Технология проблемного обучения
 Скачать 92.96 Kb. Скачать 92.96 Kb.
|
| ТЕХНОЛОГИЯ ПРОБЛЕМНОГО ОБУЧЕНИЯ Использование элементов проблемного обучения дает положительный результат, благодаря детальной проработке и осмыслению программного материала. Помогает сформировать у учащихся умение видеть проблему, формулировать её, искать варианты решения, комбинировать разные аналитические подходы, версии, позиции, синтезировать их, формулировать выводы. Знания, «добытые» учениками в ходе решения поставленных проблем, не описанных учебником, прочно осмыслялись и закреплялись. В классах, где учебные навыки выше среднего, использование данной технологии позволяет углубить знания учащихся, развивать в них способность к аналитическому мышлению. Данную технологию применяю как в младших, так и в старших классах на уроках изучения нового материала, на этапе подготовки учащихся к активному и сознательному восприятию нового материала и на этапе изучения новых знаний и способов деятельности. План-конспект урока математики в 6 классе по теме «Пропорция». Цель урока: формирование умений составлять и решать пропорции. Задачи: - образовательные (формирование познавательных УУД): создать условия для формирования умений решать пропорции, выполнять действия с десятичными дробями, составлять план решения задач по заданным условиям и в жизненных ситуациях; закрепить навыки и умения применять алгоритмы при решении задач на пропорции. - воспитательные (формирование коммуникативных и личностных УУД): научить слушать и вступать в диалог, участвовать в коллективном обсуждении проблем, интегрироваться в группу сверстников и строить продуктивное взаимодействие; уметь договариваться и приходить к общему решению в совместной деятельности, оценивать работу участников группы в тактичной форме, отражать результаты в устной и письменной речи, соблюдая правила речевого этикета, уметь использовать знаково-символические средства, воспитывать ответственность и аккуратность. - развивающие (формирование регулятивных УУД) определять и формулировать цель на уроке с помощью учителя, проговаривать последовательность действий на уроке; фиксировать собственные затруднения на уроке; проводить рефлексию собственной деятельности и деятельности группы; находить информацию; осуществлять контроль правильности действий; выбирать способы решения задач в зависимости от конкретных условий. Тип урока: комбинированный урок Формы работы учащихся: фронтальная работа, индивидуальная, работа в парах. Необходимое техническое оборудование: компьютер, мультимедийный проектор, интерактивная доска, экран. Компьютеры для каждого учащегося. Средства: учебник, рабочая тетрадь, карточки, электронная карта контроля. Учебник: Математика. 6 кл: учеб. для учащихся общеобразоват. учреждений / Н.Я. Виленкин, В. И, Жохов, А. С. Чесноков, С. И. Шварцбург.- М.: Мнемозина, 2012. ХОД УРОКА. I. Организационный момент (2 мин.) Проверить готовность учащихся класса к уроку. Отметить в журнале отсутствующих. II.Устные упражнения по карточкам(8 мин)
Оборотная сторона карточки.
Фронтальная работа. Числа изображены на карточках, которые демонстрируются учащимся поочередно. На обратных сторонах карточек записаны ответы (изображены частично пунктиром) Сопутствующие вопросы:
III. Изучение нового материала (15 мин).
-Придумайте отношения, равное 5. -Если наши отношения равны 5, я могу записать из них равенства: 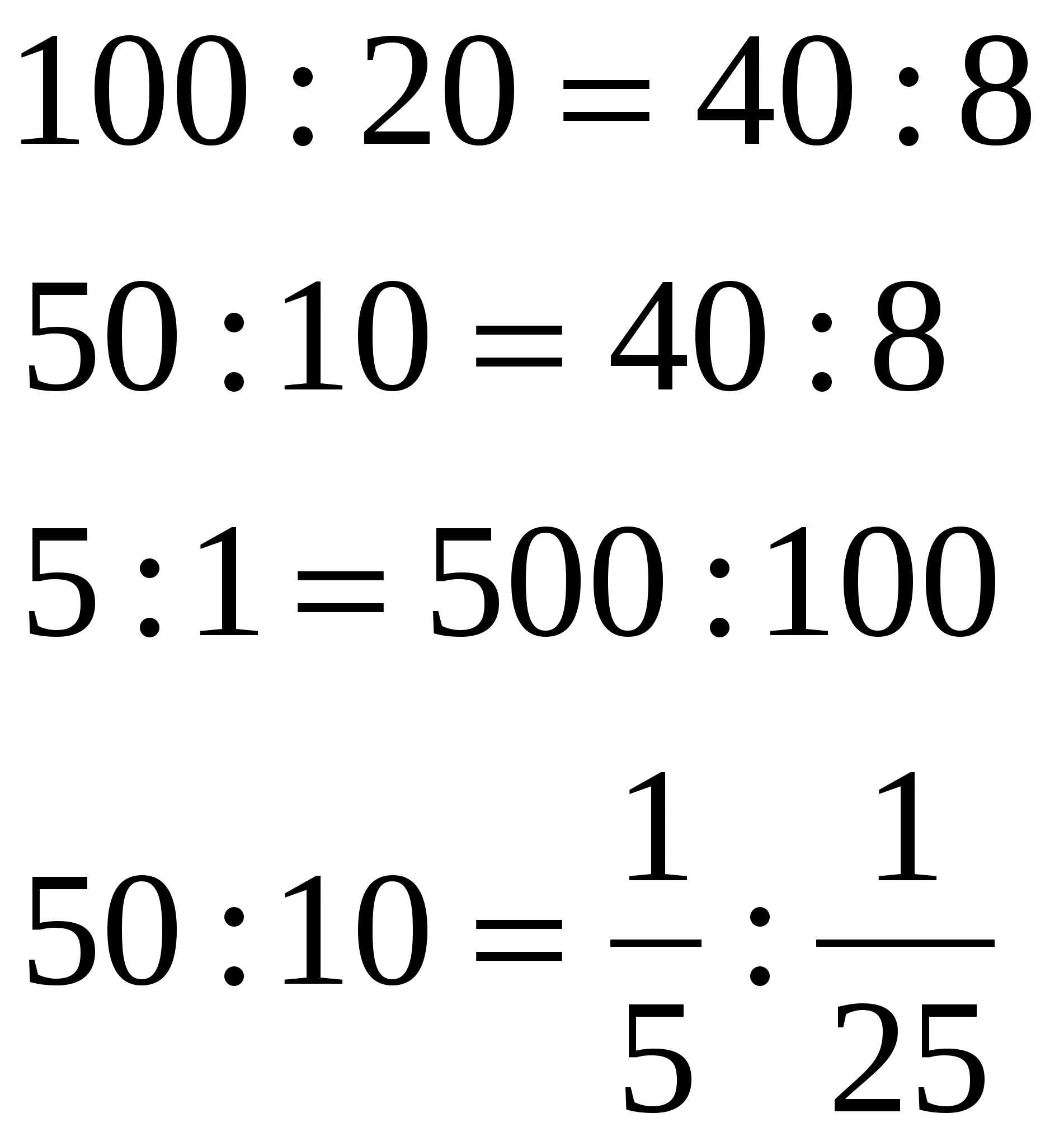 -Как по-другому можно записать равенство? (Записать частное в виде дроби.) Определение. Равенство двух отношений называют пропорцией.
Общий вид пропорции: a : b=c : d Чтение записи a : b=c : d следующее: «Отношение a к b равно отношению c к d»; Чтение записи Числа a и d называются крайними членами пропорции, а числа b и c – средними членами, a≠0, b≠0, c≠0, d≠0. - Назовите крайние и средние члены пропорций. средние  a : b = c : d  крайние Задание 1. Установить является ли пропорцией равенство: По каждой карточке задаются дополнительные вопросы; проверяются глубина знаний учащихся по теме: «Отношения» перед изучением нового материала. Вопросы к учащимся. Формулируется определение понятия пропорции записывается учащимися в тетрадь. Используется схема, изображенная на плакате. Задание записано на доске, Выполняется учениками устно а) б) Задание 2. В пропорции 2,4:0,6=8:2 найдем произведение её крайних и произведение её средних членов: 2,4·2=4,8 и 0,6·8=4,8. Получим, что 2,4·2=0,6·8. Задание 3. Найдите произведение крайних членов пропорции и произведение средних членов: а) б) -Что интересного заметили? -Какой вывод можно сделать? Вывод: Произведение крайних членов равно произведению средних членов. Итак,мы вывели основное свойство пропорции. В верной пропорции произведение крайних членов равно произведению средних. -Верно ли обратное утверждение? Сформулируйте его. Приведите свой пример.[Если произведение крайних членов равно произведению средних членов пропорции, то пропорция верна.] Запишем основное свойство пропорции: и  ли a : b = c : d; a · d= b · c. ли a : b = c : d; a · d= b · c. И обратно: если a · d= b · c, то Далее создается проблемная ситуация: Можно ли из данной пропорции составить новые пропорции? Сколько? На размышление учащимся дается две минуты, затем верное решение демонстрируется на доске Вывод делают сами ученики. Вопросы к учащимся. Запись в тетрадях учащихся.       a · d= b · c   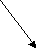      Задание 4. Используя верное равенство: 5·1,2=2·3, составьте четыре верные пропорции. Решение. Из верного равенства 5·1,2=2·3 получаем четыре пропорции: Используя основное свойство пропорции, можно найти ее неизвестный член, если все остальные члены известны. Пример 1. Найдите в пропорции n:0,6=7:2,1 неизвестный крайний член n. Решение. n:0,6=7:2,1; n·2,1=0,6·7; n= Ответ: n=2. Пример 2. Решим уравнение: 1 способ: 2 способ: 0,2·0,105=х·0,7. 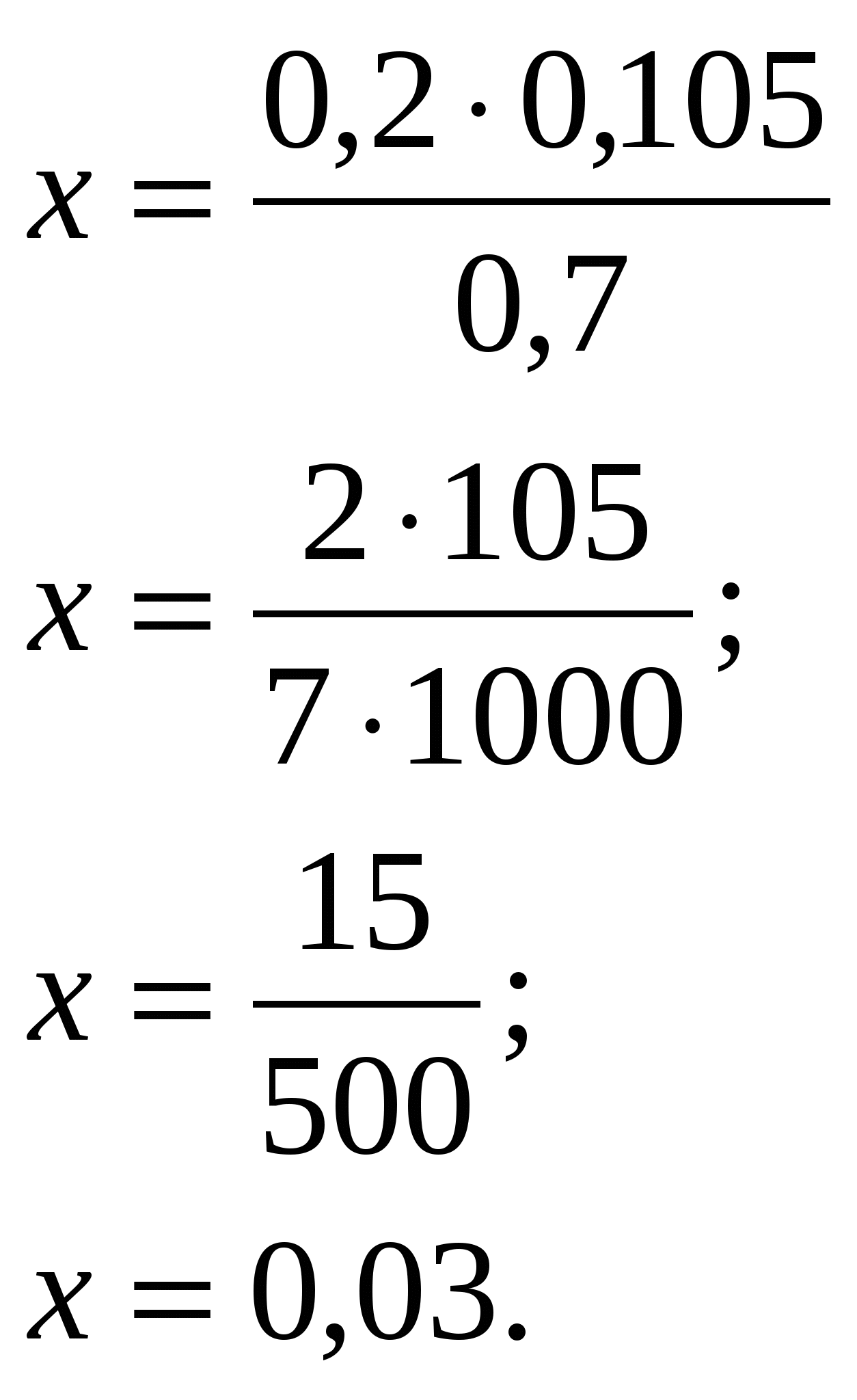 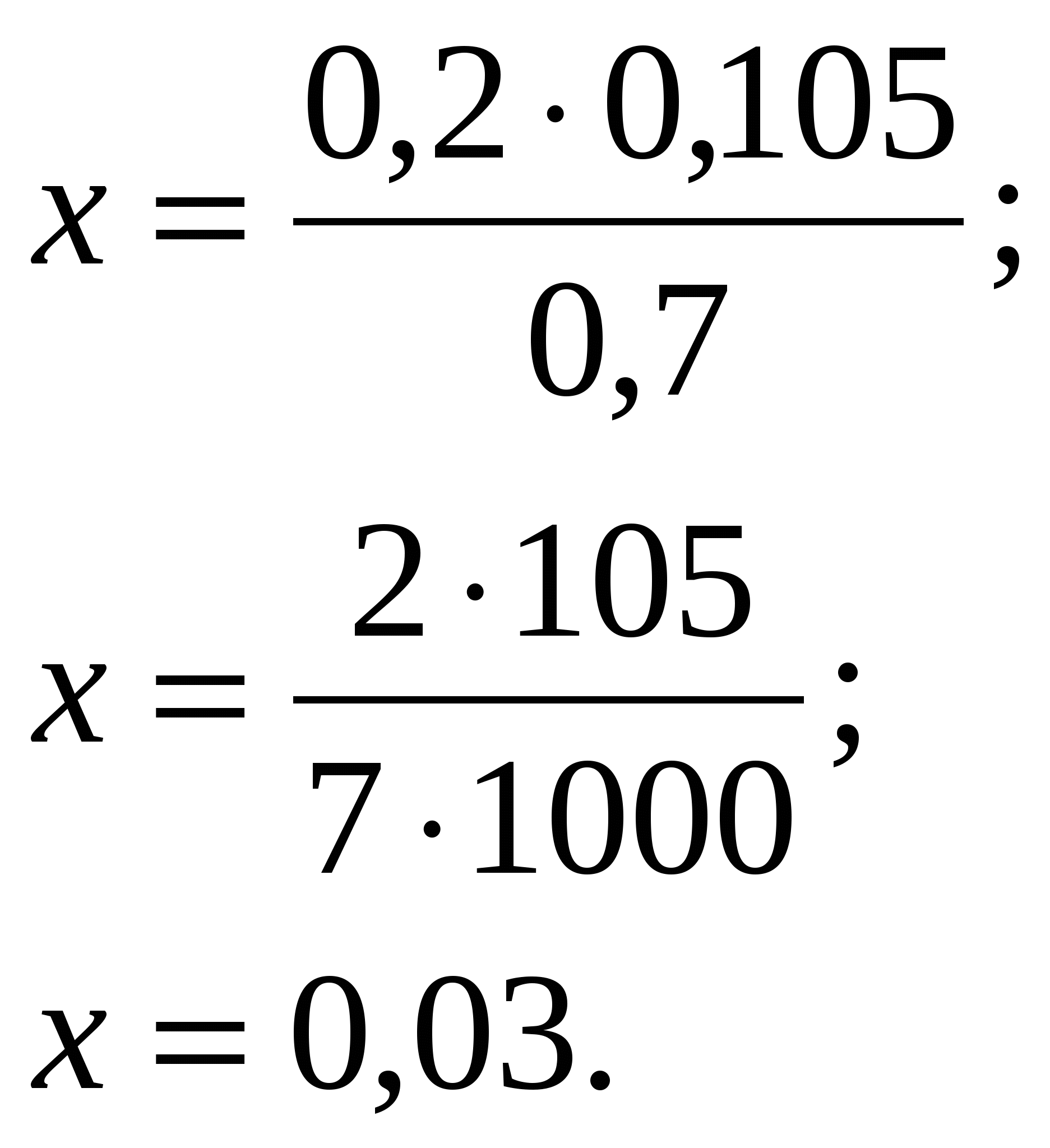 Ответ: х=0,03. Ответ: х=0,03. У доски выполняет сильный ученик Учащиеся записывают в тетрадях. ВНИМАНИЕ! Применение основного свойства пропорции при решении уравнений. Учащиеся записывают в тетрадях. IV. Закрепление изученного материала.(15 мин) №762(в, д - устно, а, е -письменно). Решение. в) неверная пропорция; д) верная пропорция; а) 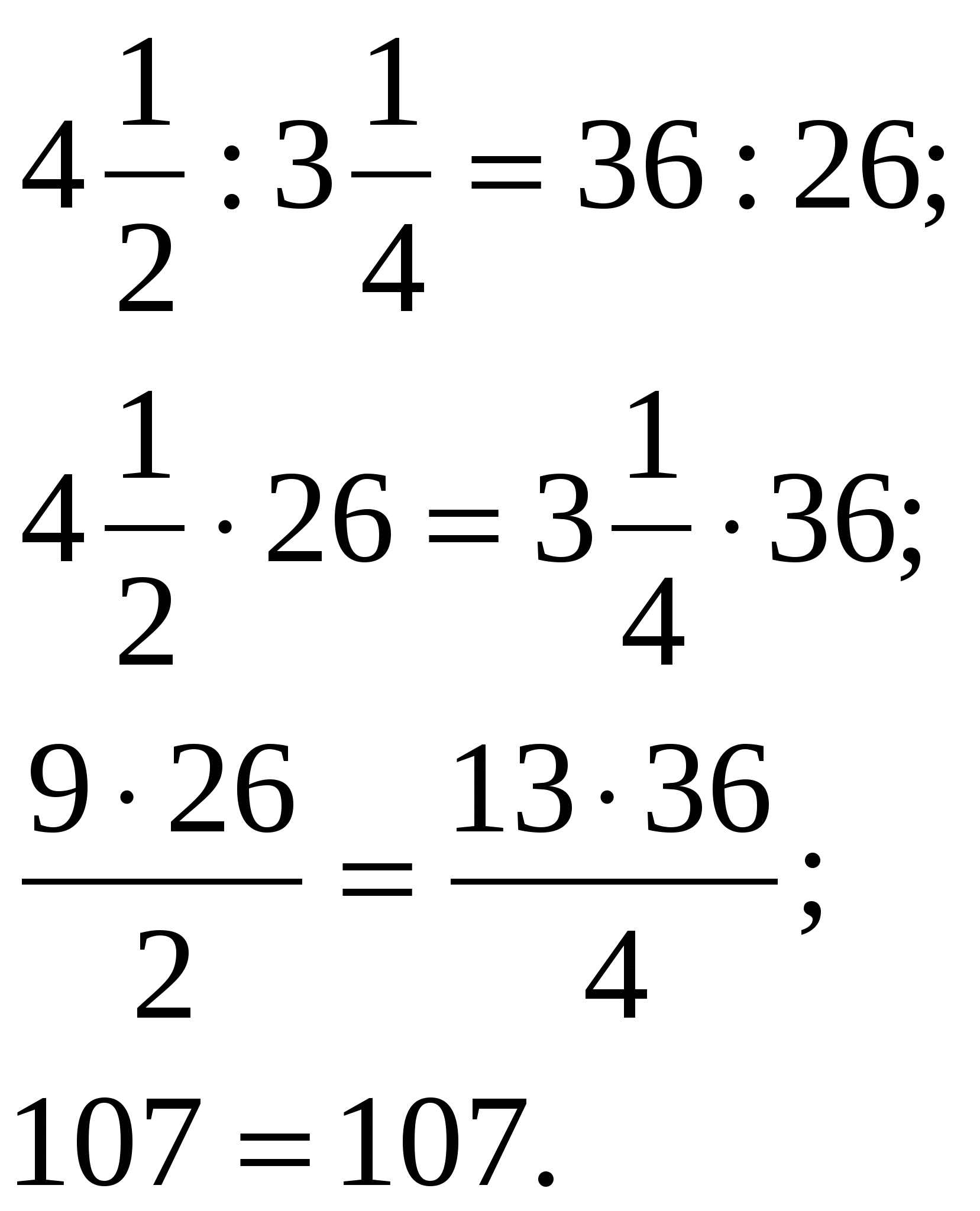 е) е) 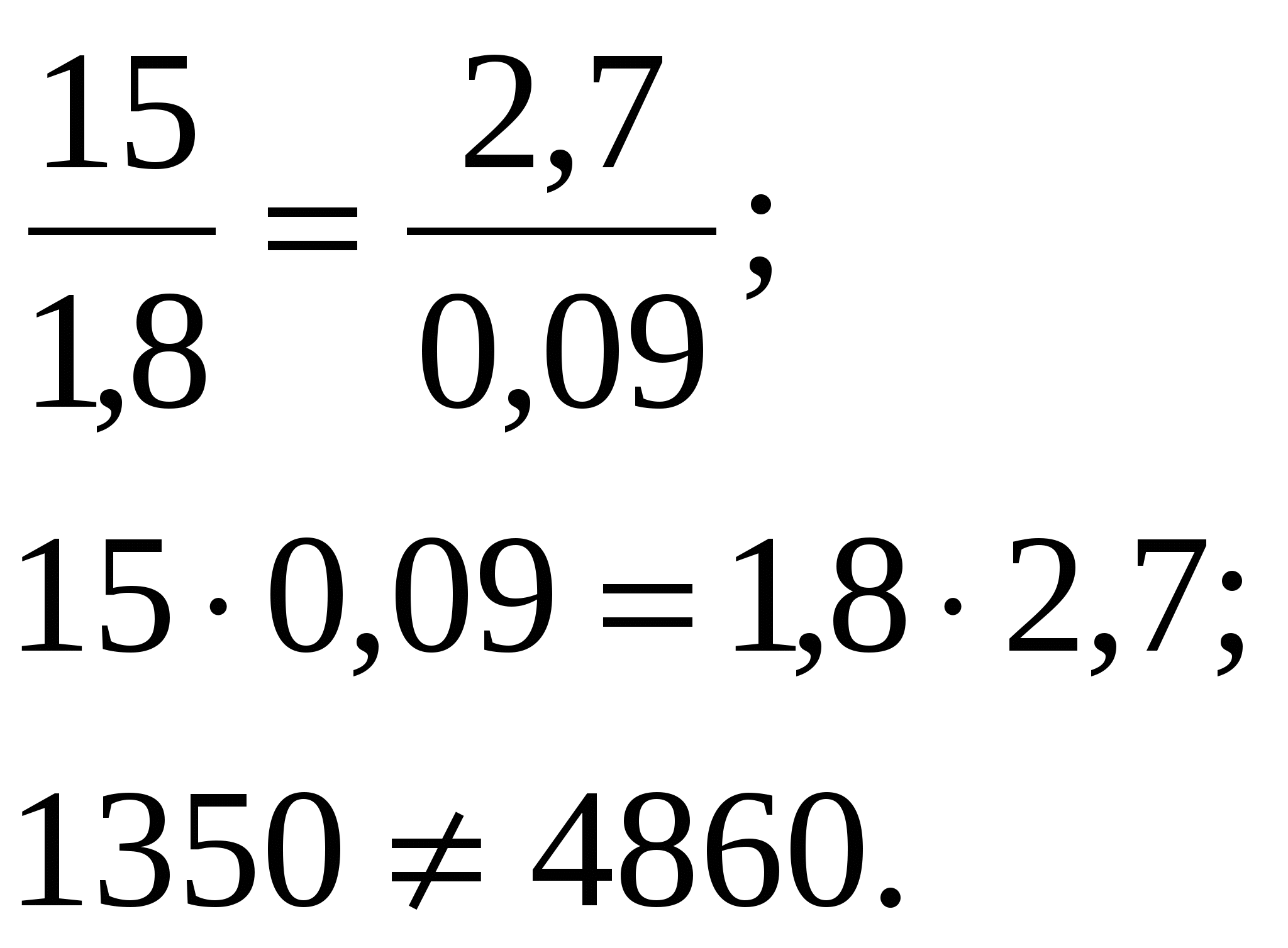 №763(в,г,д,з). Решить уравнение. Ответы. в) V. Домашнее задание (2 мин). §4, п. 21, №№776, 777(а, в), 781(а). VI. Подведение итогов урока ( 3 мин). 1. Что такое пропорция? 2. Сформулируйте основное свойство пропорции. 3. Сколько можно составить новых пропорций из данной? Сообщаются оценки учащимся.
На доске одновременно решают двое учащихся. Остальные записывают в тетрадях. Сначала решают в), г) одновременно. |