Урок по алгебре и информатике в 7-м классе Тема урока: " Квадратные уравнения. Электронная таблица"

Название	Урок по алгебре и информатике в 7-м классе Тема урока: " Квадратные уравнения. Электронная таблица"
Дата	01.03.2016
Размер	56.57 Kb.
Тип	Урок

Интегрированный урок по алгебре и информатике в 7-м классе

Тема урока: “ Квадратные уравнения. Электронная таблица”.

Цели:

воспитывать дисциплинированность, стремление к современной организации трудовой деятельности;
развивать умение применять знания в нестандартных ситуациях;
сформировать представления о квадратных уравнениях, о решении квадратных уравнений с помощью формул сокращённого умножения;
повторить формулы сокращённого умножения;
закрепить полученные знания по теме в электронной таблице «Excel».

Знания и умения:

● знать формулы сокращённого умножения, уметь разлагать на множители по формулам сокращённого умножения;

● иметь представления о квадратных уравнениях;

● уметь решать квадратные уравнения с помощью формул сокращённого умножения;

● уметь открывать документ созданный на Excel, сохранять электронную таблицу, переименовать листы;

● знать расширение файлов, содержащих электронную таблицу, знать с какого знака начинается формула.

Оборудование: динамические карточки, домино, карточки, мультимедийный проектор, компьютеры, доска.

Литература:

В. Рычков. Краткий курс Excel 2000, Санкт-Петербург 2000 г.
г. «Математика» № 42 – 2001. стр. 23.
Ю.А. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.В. Суворова. Алгебра-7.
Г.И.Глеёз. История математики в школе, Москва, 1998 г.
ж. Информатика в уроках и задачах, Москва, 2001г.
г. «Информатика» № 6 2006 г.
г. «Информатика» № 2 2005 г.

Технологии, используемые на уроке:

● технология проблемного обучения;

● групповая технология;

Ход урока.

I. Организационный момент (1 мин.)

II. Проверка домашнего задания (3 мин.)

Дома необходимо было придумать задания на формулы сокращённого умножения. До урока просматриваются тетради и выбираются наиболее интересные, для того чтобы разобрать у доски. Ученики с нестандартными творческими работами выступают у доски.

III. Отработка навыков разложения на множители с помощью формул сокращённого умножения (5 мин.)

Группа №1 (2 человека) решает задание: найти неизвестное слагаемое, чтобы получилась формула сокращённого умножения, и разложить на множители. (Заранее заготавливаются карточки, прикрепляются к доске с помощью магнитиков, в карточках отверстия в виде прямоугольников, для того чтобы ученики могли вписать недостающее слагаемое мелом).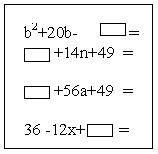

Группа №2 (4 человека) составляет домино (заранее готовятся карточки, крепятся к доске с помощью магнитиков, магнитики с обеих сторон).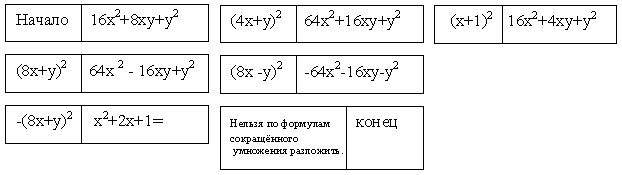

После составления домино, переворачиваю карточки. При правильном выполнении задания получится слово «МОЛОДЦЫ!»

Группа №3 (2 человека) решает задание. Найти неизвестное слагаемое, чтобы получилась формула сокращённого умножения, и разложить на множители (готовятся карточки, крепятся к доске с помощью магнитиков, в карточках отверстия в виде прямоугольников, для того чтобы ученики могли вписать недостающее слагаемое мелом.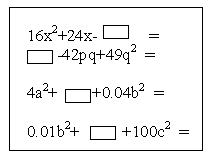

С остальными учениками устный фронтальный опрос по динамическим карточкам.

IV. Введение новой темы (9 мин.)

Заранее приготовлены примеры уравнений на другой стороне створки доски.

1) x² + 4x + 4 = 0
2) 4x² + 12x + 9 = 0
3) 3x² + 7х + 5 = 0
4) 25x² – 10x + 1 = 0
5) x² – 6x + 9 = 0
6) 8x² – 10x + 1 = 0
7) x² + 4x + 4 = 0
8) 10x² – 10x + 1 = 0
9) 16x² – 16х + 4 = 0
10) 12x² – 16х + 4 = 0

– Что общего в этих уравнениях?

– Как в общем виде записать уравнения такого вида?

Уравнения вида ax² + bx + c = 0, где х – переменная, a, b, c – некоторые числа, причем, а =/= 0 называется квадратными уравнениями.

Сегодня мы научимся решать квадратные уравнения с помощью формул сокращённого умножения. Посмотрите на доску. В каких уравнениях можно применить формулы сокращённого умножения? Подчеркиваю, в которых можно применить формулы сокращённого умножения. Неподчёркнутые уравнения мы научимся решать позже.

Стираю неподчёркнутые уравнения. Давайте решим первое уравнение? Записываю решение сама, обращаю внимание на оформление.

x² + 4x + 4 = 0

Какую формулу сокращённого умножения можно применить к левой части уравнения?

(х + 2)² = 0.

Квадрат, какого числа равен нулю?

Какой вывод можно сделать?

х + 2 = 0 х = – 2.
Ответ: – 2.

V. Закрепление новой темы (7 мин.)

1) Для решения 2, 4, 5 уравнений вызываю к доске учеников. Остальные решают самостоятельно 7, 9. Хожу по рядам, при необходимости оказываю помощь. Комментирую и оцениваю наиболее отличившихся учащихся.

2) Устно. По динамическим карточкам.

x² – 4x + 4 = 81;

(x – 2)² = 81;

х – 2 = 9 или х – 2 = –9;

x = 9 + 2 или х = –9 + 2

х = 11 или х = –7.

Ответ: 11; –7.

x² + 6x + 9 = 4;

(x + 3)² = 4;

х + 3 = 2 или х + 3 = –2;

x = 2–3 или х = –2–3

х = –1 или х = –5.

Ответ: –1; –5.

	4x² –12x + 9 = 25;
	(2x – 3)² = 25;
	2х – 3 = 5 или 2х – 3 = –5;
	2x = 5 + 3 или 2х = –5 + 3
	2х = 8 или 2х = –2;
	х = 8 : 2 или х = –2 : 2
	х = 4 или х = –1.
	Ответ: 4; –1.

64 + 16х + x² = 36;

(8 + х)² = 36;

8 + х = 6 или 8 + х = –6;

x = 6 – 8 или х = –6 – 8;

х = –2 или х = –14.

Ответ: –2; –14.

VI. Комментирование домашнего задания (1 мин.)

Придумать квадратные уравнения, которые решаются с помощью формул сокращённого умножения. Учить конспект «Excel», раздел «Вставка формул».

VIII. Актуализация опорных знаний (4 мин.)

Устный фронтальный опрос по информатике.

– Как открыть электронную таблицу?
– Какое расширение имеют файлы, содержащие электронную таблицу?
– Что можно вносить в электронную таблицу?
– Как сохранить электронную таблицу?
– Как выглядит активная ячейка электронной таблицы?
– Как составляется имя ячейки?
– Минимальный элемент электронной таблицы?
– Как переименовать листы?
– С какого знака начинается формула?

IX. Практическая работа на компьютере (12 мин.)

1) Заранее создаю документ Excel, В А1 записываю «решите уравнение», с А2 по А11 записываю не сложные квадратные уравнения с целыми корнями. В В1 по В11 пишу часть квадратных уравнений после = . В С1 пишу Х1, в D1 пишу Х2, в E1 пишу «проверка », в F1 пишу «количество балов», в G1 пишу «оценка», в Е2 пишу формулу ЕСЛИ (((с2*с2 + 2*с2 + 1) = b2)*((d2*d2 + 2*d2 + 1) = 4);истина; ложь), с Е3 по Е11 аналогично.
В F2 пишу формулу = ЕСЛИ(E2 = ИСТИНА;1;0), с F3 по F11 аналогично.
В G2 пишу формулу = F2, до G6 аналогично, в G7 пишу формулу, ЕСЛИ(F7 = 6;"'молодец'"), до G11 аналогично.

2) Решите уравнения в тетради и впишите соответствующие значения х1 и х2 в электронную таблицу.

При верном решении таблица выглядит таким образом.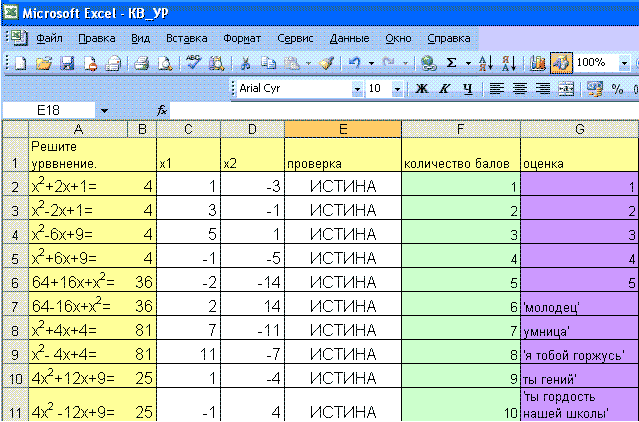

X. Подведение итога урока (3 мин.)

Какие новые уравнения мы узнали?
С помощью, каких формул мы решали квадратные уравнения?
Все ли квадратные уравнения можно решить с помощью формул сокращённого умножения?

Комментирую работу всего класса и отдельных учащихся. Записываю в журнал максимальную оценку из таблицы каждого ученика.

Урок закончен. Спасибо за урок!