Решение систем неравенств с одной переменной
 Скачать 56.65 Kb.
|
    МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕМИТЬКОВСКАЯ СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА
Разработка урока по математике для учащихся 8 класса по теме: «Решение систем неравенств с одной переменной» Учитель: Тютюнник Елена Леонидовна Тема: Решение систем неравенств с одной переменной. Предмет, класс, количество часов: Алгебра, 8 класс, 1 час. Тип урока: урок изучения нового материала. Цели урока: ОЦ: обеспечить усвоение умения решать простейшие системы, содержащие линейные уравнения с одной переменной. ВЦ: через организацию урока воспитывать активность в труде, самостоятельность. РЦ: развивать умения анализировать, сравнивать, выделять главное и обобщать. Методы обучения: объяснительно-иллюстративный, репродуктивный, частично-поисковый при нахождении, способа решения систем неравенств с одной переменной. ХОД УРОКА
Прозвенел звонок для нас! Встали все у парт красиво, Поздоровались учтиво, Тихо сели, спинки прямо. Все легонечко вздохнем. Урок алгебры начнем. Ребята, сегодня на уроке у нас присутствуют гости. Оглянитесь, посмотрите, поприветствуйте их своей улыбкой, посмотрите друг на друга, улыбнитесь, и пожелайте друг другу успехов и хорошего настроения. -Какую тему Вы изучали на прошлом уроке? (Решение неравенств с одной переменной) На прошлом уроках вы научились решать неравенства с одной переменной, используя свойства при решении неравенств. Неравенство может быть хорошим помощником. Только надо знать, когда к нему необходимо обратиться за помощью. На языке неравенств нередко формулируется постановка задач во многих приложениях математики. Например, многие экономические задачи сводятся к исследованию систем линейных неравенств. Поэтому важно уметь решать системы неравенств. Сегодня вы узнаете, как решать системы неравенств, сформулируете алгоритм решения и научитесь применять его при решении задач. А для этого я предлагаю вам быть внимательными и активными. Быть активным в труде – это, значит, поставить перед собой цель и добиться ее выполнения. Давайте сформулируем цели, которые будем решать на уроке. (Научиться решать простейшие системы, содержащие неравенства с одной переменной). Я приглашаю всех принять активное участие в достижении целей нашего урока. Запишите тему урока: «Решение систем неравенства с одной переменной». 2. Подготовка к изучению нового материала. Для того чтобы перейти к изучению решения систем необходимо вспомнить изученный ранее материал. У доски ученик решает домашний № 844(а) из учебника.(остальные ученики выполняют тест) 5(х-1)+7≤1-3(х+2) 5х-5+7≤1-3х-6 5х+3х≤1-7+5-6 8х≤-7 | :8 х≤-  - Ответ: (  ).Как решали неравенство? (используя свойства.) Перечислите свойства, используемые при решении? (открывая скобки, знаки меняем на противоположные, если перед скобкой стоит знак минус; перенося слагаемые из одной части в другу, меняем знаки; если обе части неравенства умножить или разделить на одно и то же число положительное то получится равносильное ему неравенство, если умножить или разделить на одно и тоже отрицательное число обе части уравнения, то знак неравенства нужно поменять на противоположный ). Для повторения теории темы «Неравенства и их свойства», проведем тестирование с последующей проверкой. Каждое задание теста предполагает ответ «Да» - фигура , «Нет» - фигура .
(ответ: ). Устный счет: Множество чисел, удовлетворяющих неравенству -4< х 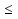 5 изображено на рисунке… Ответ:4). (слайд )Числовой промежуток ( 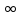 ; 9] изображен на рисунке… Ответ:3). (слайд ) Установить соответствие между неравенством и числовым промежутком (слайд ) «Математика учит преодолевать трудности и исправлять собственные ошибки». Найдите ошибку в решении неравенства, объясните почему допущена ошибка, запишите в тетрадь правильное решение. ( слайд ) Задача: Автомобиль по горной дороге за 7 часов проезжает больше 210 км, а по шоссе за 5 часов – не более 400 км. В каких пределах может изменяться его скорость? (слайд ). 7х > 210, 5х 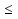400.О чем идет речь в задаче? Что требуется найти? Что обозначим за х? (скорость автомобиля) Как найти расстояние? (Скорость умножить на время.) Запишите неравенство Составление математической модели (слайд ). Постановка проблем: требуется найти такие значения х, при которых верны оба неравенства, т.е. найти общее решение этих неравенств. В таких случаях говорят, что надо решить систему неравенств, и используют следующую запись 7х > 210, 5х 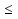400.3.Изучения новой темы - Как вы думаете, что называется решением системы неравенств? (Решением системы неравенств с одной переменной называется значение переменной, при котором верно каждое из неравенств системы) - Что значит « Решить систему неравенств»? (Решить систему неравенств – значит найти все её решения или доказать, что решений нет) - Что надо сделать, чтобы ответить на вопрос « является ли заданное число решением системы неравенств?» (Подставить это число в оба неравенства системы, если получатся верные неравенства, то заданное число является решением системы неравенств, если получатся неверные неравенства, то заданное число не является решение системы неравенств) Решить самостоятельно систему в задаче на движение автомобиля и ответить на вопрос задачи. Сформулировать алгоритм решения систем неравенств Рассмотреть примеры, 4. Закрепление темы. Работа с учебником (, 879(а), 881). 5. Домашнее задание: п.35 читать, рассмотреть примеры 1-4, решить № 876(в, г)- -880(в, г). 6. Самостоятельная работа по вариантам 7. Подведение итогов урока (выставляются оценки) Рефлексия (яблоня): - Какую тему рассмотрели сегодня на уроке? - В чем испытали затруднения? - Над чем необходимо еще поработать? |
?