Решение квадратных уравнений
 Скачать 52.3 Kb. Скачать 52.3 Kb.
|
| Тема урока: Решение квадратных уравнений. Цели урока: систематизация знаний по теме; расширение представлений учащихся о способах решения квадратных уравнений; формирование коммуникативных умений при работе в парах; выработка вычислительных навыков; развитие познавательного интереса, внимательности, наблюдательности, инициативы, навыков исследовательской деятельности. Тип урока: комбинированный. Методы урока: словесный, наглядный, частично-поисковый. Формы организации деятельности: индивидуальная, коллективная, парная Оборудование: экран, проектор, карточки-задания, презентация. План урока.
Ход урока. 1. Организационный момент. «Посредством уравнений, теорем Я уйму всяких разрешил проблем». Чосер (СЛ.№1) Квадратные уравнения - это фундамент, на котором покоится алгебра. Используются широко не только в смежных дисциплинах (геометрии, химии, физике, астрономии), но и являются могучим средством для решения вопросов производства ,строительства, народного хозяйства. Поэтому на уроке мы систематизируем известные методы решения квадратных уравнений и овладеем новым. Сообщение плана урока. 2. Актуализация опорных знаний 5 человек индивидуально работают у доски, решают квадратные уравнения изученными способами. (Цель: проверка усвоения и анализ изученных способов решения квадратных уравнений ). 5х2-8х-4=0 (формулы корней 1); 5х2-8х-4=0 (формулы корней2) ; 5х2-8х-4=0 (выделение квадрата двучлена); Х2-5х+6=0( разложение на множители); Х2-5х+6=0(графический способ). Остальные учащиеся класса работают в парах над « Вопросами для размышления» (Цель: активизация мыслительной деятельности, формирование коммуникативных и логических учебных действий) Вопросы к размышлению. 1.В каком случае уравнение вида ах2 + вх + с=0 является квадратным? 1)в≠0; с≠0;а=0; 2) а≠0; 3)в≠0; с≠0. 2.Уравнение ах 2+вх+с=0 (а≠0) имеет два различных действительных корня, если: 1)Д≥0; 2) Д>0; 3)Д=0; 4)Д<0. 3.Коля забыл тетрадь с домашним заданием и утверждает, что уравнение х2-3х+2=0 решал графическим способом; помнит, что графики пересекаются в двух точках. Убедитесь, что Коля выполнял домашнюю работу. 4.Смекалкин взглянул на уравнение вида ах 2+ с=0 и сделал вывод: корней нет. Мог ли он это утверждать, не решив уравнение? 5.В домашнем задании было предложено уравнение ( х2-5х-1)2-3(х2-5х-1)+2=0. Подумав, Витя рассудил: сначала раскрою скобки, приведу подобные слагаемые, а затем применю формулы корней. Согласны ли вы с Витей? (СЛАЙДЫ № 3-4) . Цель: повторение теории, выделение существенных признаков. При коллективном обсуждении отвечают на вопросы:1)почему не может быть верным ответ а)? 2)назовите формулу дискриминанта; 3) как изменить формулировку задания, чтобы верным был ответ 4)? Рассмотреть решения заданий на доске и проанализировать применённые методы решений. Как вы думаете, зачем нужны различные способы решения? (есть возможность выбрать наиболее рациональный) К чему он приведет? (даст экономию времени), а где она особенно нужна? (на экзаменах, на других уроках) 3.Изучение нового материала. Запишите дату и тему урока «Решение квадратных уравнений». (СЛАЙД №2) (СОЗДАНИЕ ПРОБЛЕМНОЙ СИТУАЦИИ) Решите уравнение: 1000х2-1193х+193=0. Укажите способ решения. ( Использование формулы корней). Спрогнозируйте, с какими трудностями вы встретитесь в процессе работы (коэффициенты большие, вычисления громоздкие). Какой выход? ( искать другой метод решения) Слайд №5 ( Лучший способ изучить что-либо - это открыть самому. Д. Пойа) Учащиеся по карточкам решают самостоятельно уравнения (по вариантам), вносят в таблицу значения коэффициентов , их сумму, найденные корни. (Развитие навыков исследовательской деятельности) (СЛАЙД №6)
Что вы заметили? Какие уравнения имеют корень, равный 1(-1)? Как получен второй корень? Какую гипотезу выдвинем? 1. Если в квадратном уравнении ах2 + вх+с=0 а+в+с=0,то х1=1,а х2= 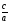 . . 2. Если в квадратном уравнении ах2 + вх+с=0 а-в+с=0,то х1=-1,а х2= - 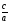 . (СЛАЙД №7) . (СЛАЙД №7)А как подтвердить предположения? Подставить корни в уравнение ( один из учащихся проводит доказательство у доски). Попробуйте дать название новому методу решения ( метод на основе зависимости между коэффициентами). Возвратимся к уравнению 1000х2-1193х+193=0: а=1000; в=-1193; с=193; а+в+с=1000-1193 +193=0  х1=1,а х2= - х1=1,а х2= -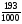 . Ответ: 1; 0,193. . Ответ: 1; 0,193.Решите уравнение: 20х2-3х-23=0: а=20;в=-3;с=-23; а-в+с=20-(-3)-23=0  х1=-1; х2=- х1=-1; х2=- =1,15. Ответ:-1; 1,15. =1,15. Ответ:-1; 1,15.4.Закрепление знаний. «Скажи мне - и я забуду, Покажи мне - и я запомню, Дай мне действовать самому - и я научусь» Конфуций. (Слайд №8) Учащиеся выполняют самостоятельную работу по вариантам. (Цель: первичное закрепление знаний, развитие навыков самоконтроля, творческой деятельности). (Слайд №9) Первый вариант. 1.Среди уравнений найдите те, для которых а+в+с=0 и решите их: а) 2х2-3х+1=0; б) 4х2-3х+1=0; в) - х2 + 6х-5=0; г) 5х2-6х-1=0. 2.Поставьте вместо звёздочки число так, чтобы сумма а-в+с=0 и решите уравнение: а) 4х2+5х-*=0. 3.Придумайте квадратное уравнение вида ах2 + вх+с=0, в котором а+в+с=0 и решите его. Второй вариант. 1.Среди уравнений найдите те, у которых а-в+с=0 и решите их: а) 4х2-3х-7=0; б) 8х2-5х-3=0; в) - х2+3х+4=0; г) 11х2-6х+5=0. 2.Поставьте вместо звёздочки число так, чтобы сумма а+в+с=0 и решите уравнение: 7х2+*х-9=0. 3. Придумайте квадратное уравнение, в котором а-в+с=0 и решите его. Ответы к самостоятельной работе. (Слайд №10) Первый вариант.
в)-х2+6х-5=0; а + в +с = -1+6-5=0; х1=1; х2=5. 2. *=-1; 4х2+5х+1=0; а-в+с=4-5+1=0; х1=-1, х2=- ¼ =- 0,25. Второй вариант.
в) - х2+3х+4=0; а-в+с=-1-3+4=0; х1=-1; х2=4. 2.*=2; 7х2+2х-9=0; а+в+с=7+2-9=0; х1=1; х2=-9/7=-12/7. Самопроверка через проектор. Самооценка результатов(№1- «хорошо»,№1,2-«молодец», №1,2,3- «умница») Какой метод добавим в копилку методов решения квадратных уравнений? Понравился ли вам новый метод? (Слайд №11) 5. Домашнее задание. 1. №534 (решить на основе зависимости между коэффициентами) 2. Уравнение х2-5х+4=0 решить тремя способами. 3. Творческое задание: в сети интернет найти другие способы решения квадратных уравнений, создать презентацию. 6. Рефлексия.1. Выставление оценок за урок. 2.С каким чувством вы уходите с урока? ( Выберите и прикрепите смайлик на доску).    1.Урок понравился, я овладел новым методом решения квадратных уравнений, справился с самостоятельной работой. 2.Я работал на уроке с удовольствием, я узнал много нового, удивлён, что существует столько методов решения квадратных уравнений. 3.Я старался, но испытывал затруднения. Источники информации. 1. Алгебра. 8 класс: учебник для общеобразоват. учреждений/ Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков , С.Б. Суворова под ред. С.А. Теляковского.М.:Просвещение,2007. 2. Алгебра. Дидактические материалы. 8 класс./ В.И.Жохов, Ю.Н.Макарычев, Н.Г.Миндюк-14изд.-М.:Просвещение,2009. 3.В мире уравнений. Никифоровский В.А.-М.: Наука,1987. Подготовила Милько Т.В., учитель математики МБОУ СОШ№6 г.Ноябрьск. |