Неполные квадратные уравнения
 Скачать 84.31 Kb.
|
  ОПРЕДЕЛЕНИЕ КВАДРАТНОГО УРАВНЕНИЯ.НЕПОЛНЫЕ КВАДРАТНЫЕ УРАВНЕНИЯ 8 класс учитель математики: Бачурина Е.Г. тип урока: изучение новой темы. оборудование: проектор, таблицы. обучающие
развивающие
воспитание общей культуры, умение работать в коллективе. Цели: (слайд №2)
Ход урока. I. Подготовка учащихся к восприятию нового материала. (слайд №3)
II. Изложение нового материала. 1) слайд №4. Перед учащимися различные уравнения. Их задача выбрать квадратные уравнения (по их мнению). С помощью наводящих вопросов, вывести вид квадратного уравнения. (Наводящие вопросы: какая информация спрятана в название «квадратные уравнения», переменные каких степеней могут содержаться в квадратном уравнение, может ли это уравнение содержать степень меньше 2, больше 2, что еще может содержать такое уравнение, попробуем записать с помощью букв и т.д.) 5х + 26 = 8х - 3, 9х + 7х^4 - 13 = 0, 4x^2 + 22x - 2 = 0, x^3 - 42x - 29 = 0, x^4 - 13 = 0, -3x^2 - 35x + 14 = 0, 2x^2 - 53x + 12 = 0, x^2 + 22 - 5x = 0, 9x + 2x^2 - 17 = 0, -7x^4 - 46x + 17 = 0, 15x^2 - 8x^3 = 3, 8x - 6x^2 = 0, 34 + 5x^3 - 22х = 11, 25x^3 - 4x - 9x^4 = 0, Когда определены квадратные уравнения и с помощью вопросов на доске записан общий вид квадратного уравнения, появляется слайд №5.Уравнение вида ах2+bх+с=0, где а  0, x - переменная, а,b,с – некоторые числа, называют квадратным уравнением, например, ах2+bх+с=0 или ах2+вх1+сx0=0 называют квадратным уравнением;а - I коэффициент, в – II коэффициент, с – коэффициент свободного члена. На опорной доске вывешивается таблица с определением квадратного уравнения. 2)Научиться определять коэффициенты квадратного уравнения. слайд №4. (на слайде остались только квадратные уравнения). На данных уравнениях прокомментировать чему равно а, в и с. Затем обратная операция: по коэффициентам составить квадратное уравнение. слайд №6. На нем даны коэффициенты, нужно по ним составить квадратное уравнение. Как только ученик правильно составляет уравнение, на слайде, рядом с коэффициентами появляется запись этого уравнения. a = 3, b = -7, c = 12 a = -9, b = 23, c = -11 a = 8, b = 0, c = 0 a = 5, b = -22, c = -3 a = -4, b = 1, c = 5 a = 4, b = 9, c = 0 a = 1, b = 7, c = 1 a = -3, b = 0, c =15 a = -3, b = -1, c =7 a = 4, b = 0, c = 3 Когда все уравнения составлены, то полные квадратные уравнения исчезают, а те, где какой-либо из коэффициентов равен нулю, остаются. Вопросы к учащимся: Почему эти уравнения остались, что их объединяет, как могли бы называться уравнения, где есть нулевые коэффициенты. Совместно с учащимися дается определение неполного квадратного уравнения. 3)Определение неполного квадратного уравнения. слайд №7. Если в квадратном уравнении aх^2+bx+c=0 хотя бы один из коэффициентов b или с равен нулю, то такое уравнение называют неполным квадратным уравнением. (На опорной доске вывешивается определение неполного квадратного уравнения). Неполные квадратные уравнения бывают трех видов:
На доске разбирается решение уравнений слайд №6. 1. 8x^2 = 0 x^2 = 0 x = 0 Ответ: 0. Вывод: уравнение вида ах2=0, где а = 0 и в = 0, имеет один корень х = 0. На опорной доске вывешивается плакат с общим решением данного вида уравнений. ах2=0 х2=0 х=0 2. 4x^2 + 9x = 0 x( 4x + 9) = 0 х = 0 или 4х + 9 = 0 х = - 2,25 Ответ: -2,25; 0. Вывод: уравнение вида ax^ + bx = 0, где с = 0, имеет два корня: 0 и - b/a. На опорной доске вывешивается плакат с решением данного вида уравнений. ах2+bх=0 х (bх+с)=0 х=0 или bх+с=0 3. -3x^2 + 15 = 0 -3x^2 = - 15 x^2 = 5 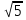x = -  x = 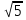Ответ: - 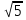; 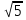4. 4x^2 + 3 = 0 4x^2 = -3 x^2 = - ¾ Ответ: нет корней. Вывод: уравнение вида ax^2 + c = 0, где b = 0, имеет два корня: - 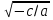 ; 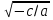если коэффициенты a и с разных знаков; и нет корней, если a и с одного знака. На опорной доске вывешивается плакат с решением данного вида уравнений. aх2+с=0 ах2=-с х2=-с:а х = 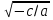 ; если а и с - разных знаков;нет корней, если а и с - одинаковые знаки. III. Закрепление нового материала. (слайд №8). Для закрепления нового материала учащиеся делятся на два варианта, каждый вариант должен решить по 10 уравнений (уравнения и ключ с решениями на слайде №8). Когда ученик получает ответ, то, с помощью ключа, определяет букву и ставит его под номером уравнения, для этого на доске записан ряд чисел: 1 2 3 4 5 6 7 8 9 10 10 9 8 7 6 5 4 3 2 1 П Р И В Е Д Е Н Н О Е У Р А В Н Е Н И Е 1 вариант начинает слева, 2 вариант начинает справа подставлять буквы под числами. У каждого варианта есть свой консультант, который в случае затруднения, помогает или объясняет решение. Если консультант не справляется, то помогает учитель. В результате правильного решения на доске появляется словосочетание ПРИВЕДЕННОЕ УРАВНЕНИЕ. 4) Вводится определение приведенного квадратного уравнения. (слайд № 9) Определение приведенного квадратного уравнения. Приведенным квадратным уравнением называют квадратное уравнение, в котором коэффициент при х2 равен 1: х2 +bx+c=0 IV. Обобщение проделанной работы. (слайд №2) Возвращаемся к целям которые стояли перед учащимися в начале урока, анализируем достигнуты ли цели, все ли удалось сделать. 1. Вывод: обеспечить для себя
2. Выставление оценок за урок. V. Задание на дом. (слайд №11) П.21, № 513 (УСТНО), № 515 (б, г, е), № 517 (б, г, е). VI. (слайд №№12-13) из истории квадратных уравнений.
В Древней Индии уже в 499 году были распространены публичные соревнования по решению задач на составление квадратных уравнений. Одной из таких задач является задача знаменитого индийского математика Бхаскары: Обезьянок резвых стая Всласть поевши, развлекаясь, Их в квадрате часть восьмая На поляне забавлялась. А двенадцать по лианам Стали прыгать, повисая. Сколько было обезьянок Ты скажи мне в этой стае? Вопрос: Составьте квадратное уравнение для решения этой задачи. ( x^2/8 + 12 = x) Ученик, первым составивший уравнение, получает оценку. Так же можно предложить подумать над составлением уравнения дома. Литература:
wiki.pskovedu.ru/.../Исторические_сведения_о_квадратных_уравн... |