Работа над уравнениями в начальной школе. Подготовила учитель начальных классов
 Скачать 85.73 Kb. Скачать 85.73 Kb.
|
| М  униципальное бюджетное общеобразовательное учреждение униципальное бюджетное общеобразовательное учреждение"Средняя общеобразовательная школа N135" имени академика Б.В.Литвинова" Работа над уравнениями в начальной школе. Подготовила учитель начальных классов: Самойлова Анжелика Владимировна г.Снежинск Работа над уравнениями в начальной школе. Большую трудность для младшего школьного возраста представляет умение решать уравнения. Изучение уравнений в начальной школе носит пропедевтический характер. Поэтому очень важно подготовить детей в начальной школе к более глубокому изучению уравнений в старших классах. В начальной школе в процессе работы над уравнением закрепляются правила о взаимосвязи части и целого, сторон прямоугольника с его площадью, формируются вычислительные навыки и понимание связи между компонентами действий, закрепляется порядок действий и формируется умения решать текстовые задачи, идет работа над развитием правильной математической речи. На уроках закрепления уравнения позволяют разнообразить виды заданий. Изучение уравнений начинается с подготовительного этапа уже в 1 классе, когда дети, действуя с предметами, решают такие «задачи»:  Затем учащиеся переходят к действиям над числами и выполняют задания, связанные с нахождением неизвестного числа в «окошке», например:  Дети находят число либо подбором, либо на основе знаний состава числа. На данном этапе учителю необходимо включать в устные упражнения следующие задания: - Сколько надо вычесть из 3, чтобы получилось 2? - Сколько надо прибавить к 2, чтобы получилось 4? На втором этапе учащиеся знакомятся с понятиями «уравнение» и «корень уравнения». На протяжении нескольких уроков дети учатся решать уравнения с неизвестным слагаемым, уменьшаемым, вычитаемым. Названия компонентов арифметических действий были введены в речевую практику учащихся и использовались для чтения равенств и выражений, пока правило нахождения неизвестного компонента в уравнениях не заучивается. Уравнения решаются на основе взаимосвязи между частью и целым. При изучении данной темы дети должны научиться находить в уравнениях компоненты, соответствующие целому (сумма, уменьшаемое), и компоненты, соответствующие его частям (слагаемое, уменьшаемое, разность). При решении уравнений детям нужно будет вспомнить лишь два известных правила: - Целое равно сумме частей. - Чтобы найти часть, надо из целого вычесть другую часть.  Эту работу облегчает графическое обозначение части ______ и целого , а также понимание того, что целое – это большее число. Для того чтобы облегчить работу над формированием навыка решения уравнений, можно проводить в классе следующую работу.
 9 9Х 7 2. Составление и решение уравнений с помощью модели числа. - Решите уравнение: Х + D : : = DDD : : Х = DD - Замените модели числами: Х + 14 = 34 Х = 20 3. Уравнения с буквами. - Как из волка получить вола? ВОЛК – Х = ВОЛ Х = ВОЛК – ВОЛ Х = К 4. Составление и решение уравнений с помощью числового луча. 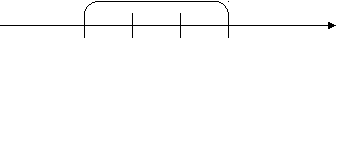 +Х +Х
5. Выполни проверку и найди ошибку. Х + 8 = 16 Х= 16 + 8 Х = 24 Дети решают: 24 + 8 = 16 32 ≠ 16 6.Составиьуравнения с числами Х, 4, 10 и реши их. Дети решают: Х + 4 = 10; 10 – Х = 4; Х – 10 = 4 и т.п. 7. Из данных уравнений реши те, где Х находится сложением. Х +16 = 20; Х -18 = 30; 29 – Х = 19 8. Рассмотри решение уравнения и вставь соответствующий знак. Х ? 12 = 23 Х = 23 – 12 К концу изучения темы дети учатся комментировать уравнения через компоненты действий. Работа строится следующим образом: 1) читаю уравнение; 2) нахожу известные и неизвестные компоненты (части и целое); 3) применяю правило (по нахождению части или целого); 4) нахожу, чему равен Х; 5) комментирую через компоненты действий. Следующий этап – решение уравнений вида: а ∙ Х = в; а : Х = в; Х : а = в. Уравнения этого вида решаются на основе взаимосвязи между площадью прямоугольника и его сторонами. Поэтому изменяется и графическое обозначение компонентов уравнения:  - площадь прямоугольника, а _____ - его стороны. Здесь важно понять то, что обучение решению и комментированию уравнений ведется по определенной схеме: - площадь прямоугольника, а _____ - его стороны. Здесь важно понять то, что обучение решению и комментированию уравнений ведется по определенной схеме:1 этап: Решение с одновременным комментированием правил нахождения площади и  его сторон. Например, Х : 2 = 5 ( Х – площадь прямоугольника, 2 и 5 – его стороны). его сторон. Например, Х : 2 = 5 ( Х – площадь прямоугольника, 2 и 5 – его стороны).Х = 2 ∙ 5 (чтобы найти площадь прямоугольника, надо перемножить его стороны) Х = 10 2 этап: Решение уравнений с комментированием(через площадь прямоугольника и его стороны). Комментирование через компоненты действий после решения уравнения. Для отработки навыков решения уравнений на умножение и деление можно использовать следующие упражнения. 1. Выполни проверку и найди ошибку. Х : 2 = 4 Х = 4 : 2 Х = 2 Дети решают: 2 : 2 = 4 1 ≠ 4 2  . Проанализируй решение уравнения и найди ошибку. . Проанализируй решение уравнения и найди ошибку.Х ∙ 3 = 9 Х = 3 ∙ 9 Х = 27 Ошибки: 1) 9 – это площадь, на целое, ее надо обозначить прямоугольником; 2) Х – это сторона, надо площадь разделить на другую сторону. 3. Составь уравнения с числами 3, Х, 12 и реши их. Дети составляют: 12 : Х = 3; 3 ∙ Х = 12 и т.п. 4. Изданных уравнений реши те, которые решаются делением. Х ∙ 2 = 6; Х : 4 = 16; 12 : Х = 4 5. Рассмотри решение уравнений и вставь соответствующий знак в запись уравнения. Х ? 6 = 24 Х = 24 : 6 6. Составь и реши уравнение: - Какое число надо умножить на пять, чтобы получилось 25? 7. Реши: Х ∙ 3 = 15; Х : 4 = 5; 16 : Х = 2 - Какое уравнение лишнее? Объясни свой выбор. Дети объясняют: - первое уравнение – Х равен нечетному числу; - второе уравнение – Х находим умножением; - третье уравнение – неизвестен второй компонент и т.п. Последний этап при работе с уравнениями в начальной школе – знакомство учащихся с составными уравнениями. Решение таких уравнений строится на качественном анализе выражения, стоящего в левой части уравнения: какие действия указаны в выражении, какое действие выполняется последним, как читается запись этого выражения, какому компоненту этого действия принадлежит неизвестное число и т.п. К этому времени учащиеся должны твердо овладеть следующими умениями: - решение простых уравнений, - анализ решений уравнений по компонентам действий, - чтение записи выражений в два – три действия, - порядок выполнения действий в выражениях со скобками и без них. На данном этапе дети должны понимать, что в записи уравнений в качестве неизвестного числа могут использоваться различные буквы латинского алфавита, например: К + 4 = 3; Р – 3 = 8; Z : 7 = 6 и т.п. Запись решения уравнений сопровождается словесным описанием выполняемых действий. Для выработки правильной математической речи и навыков решения первых уравнений данного вида необходимо использовать таблицы с образцами решений. Но так как дети уже с 1-го класса знакомы с записью различных алгоритмов, то можно использовать только алгоритм решения уравнений, по которому дети и анализируют уравнения. Алгоритм решения составного уравнения: 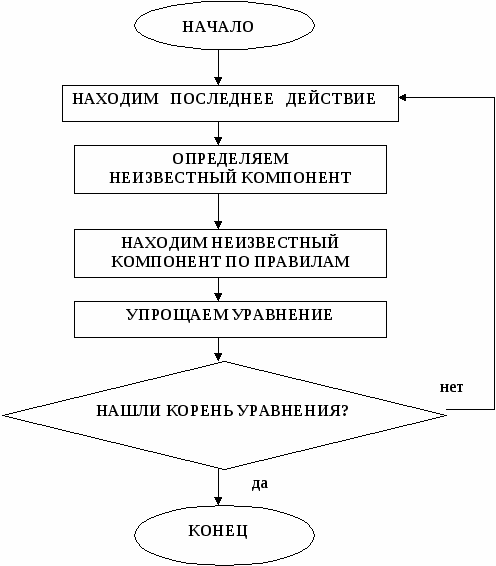 При решении таких уравнений учитель должен уделять особое внимание проверке. В начальной школе следует формировать умение выполнять проверку сначала письменно, а затем уже и устно. Ведь приучать детей к самоконтролю необходимо с первого класса. Порой учитель может видеть, как дети бездумно подставляют вместо неизвестного числа его значение и только переписывают ответ (не выполняя саму проверку). Чтобы проверка выполнялась детьми при самостоятельной работе, необходимо «заставить» каждого ребенка сделать ее (т.е. поработать над ней). Алгоритм решения уравнений на основе части и целого. 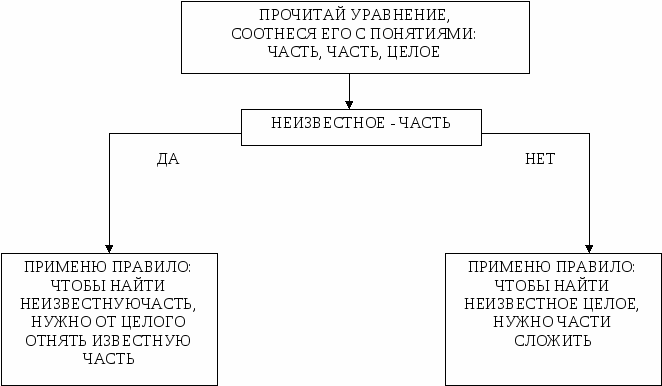 Алгоритм решения уравнений на основе части и целого. 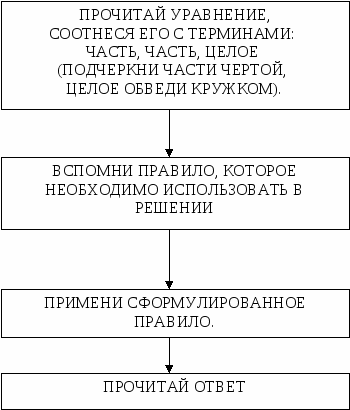  3 + Х = 7 Х = 7 – 3 Х = 4 1. 3 – часть, Х – часть, 7 – целое (3 и Х подчеркну, 7 обведу кружком). 2. Чтобы найти неизвестную часть, нужно от целого отнять известную часть. 3. 7 – 3 = 4 4. 4. Алгоритм решения уравнений на основе взаимосвязи между компонентами и результатами арифметических действий. 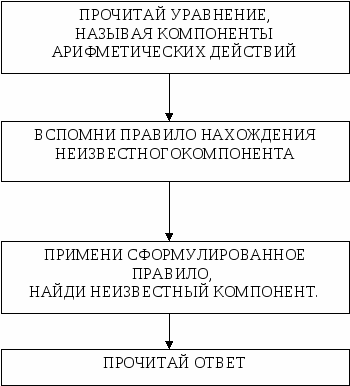 Х + 28 = 53 Х = 53 – 28 Х = 25
Алгоритм решения уравнений на основе взаимосвязи между площадью прямоугольника и его сторонами. 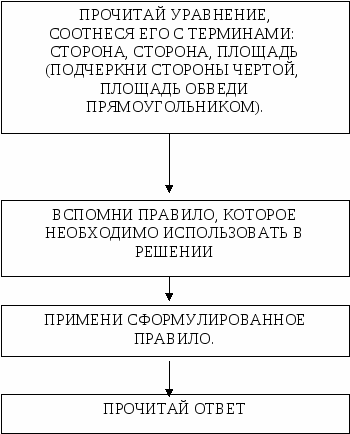  3 ∙ Х = 21 Х = 21 : 3 Х = 7 1. 3 – сторона, Х – сторона, 21 – площадь (3 и Х подчеркну, 21 обведу прямоугольником). 2. Чтобы найти неизвестную сторону, нужно площадь разделить на известную сторону. 3. 21 : 3 = 7 4. 7 – корень уравнения. Алгоритм решения уравнений на основе взаимосвязи между площадью прямоугольника и его сторонами.   ПРОЧИТАЙ УРАВНЕНИЕ, СООТНЕСЯ ЕГО С ПОНЯТИЯМИ: СТОРОНА, СТОРОНА, ПЛОЩАДЬ НЕИЗВЕСТНОЕ - СТОРОНА ПРИМЕНЮ ПРАВИЛО: ЧТОБЫ НАЙТИ НЕИЗВЕСТНУЮ СТОРОНУ, НУЖНО ПЛОЩАДЬ РАЗДЕЛИТЬ НА ИЗВЕСТНУЮ СТОРОНУ ПРИМЕНЮ ПРАВИЛО: ЧТОБЫ НАЙТИ НЕИЗВЕСТНОЕ - ПЛОЩАДЬ, НУЖНО СТОРОНЫ ПЕРЕМНОЖИТЬ   ДА НЕТ  |