Программа «Основы смыслового чтения и работа с текстом»
 Скачать 168.2 Kb. Скачать 168.2 Kb.
|
       Работа с текстом на уроках математики Работа с текстом на уроках математикиПлотникова Г.В., учитель математики МКОУ «Сибирская СОШ №1» Омский район, Омская область Актуальной междисциплинарной учебной программой, предусмотренной новыми образовательными стандартами, является программа «Основы смыслового чтения и работа с текстом». Программа направлена на формирование и развитие основ читательской компетенции, необходимой учащимся для осуществления своих дальнейших планов, в том числе, продолжения образования и самообразования, подготовки к трудовой и социальной деятельности. Сегодня умение читать не сводится только к овладению техникой чтения, а ориентировано в первую очередь на формирование «грамотности чтения». Понятие «грамотность чтения» включает способность человека понимать и использовать письменные тексты, размышлять о них и заниматься чтением для того, чтобы достигать своих целей, расширять свои знания и возможности, участвовать в социальной жизни. Одним из решений этой проблемы является организация систематической работы с учебником математики на каждом уроке и дома по трем этапам: до чтения, во время чтения и после чтения. К ключевым направлениям формирования умений работы с текстом относят следующие: Y – YI классы
YII – YIII классы
IX – XI классы
Работу по формированию умений и навыков самостоятельного чтения и понимания текста необходимо начинать с 5-го класса и проводить в системе, усложняя приемы и способы чтения и обработки информации от класса к классу. 1 этап – Работа до чтения. В начале урока можно предложить игру «Попробуй найти!», в ходе которой учитель сообщают классу название главы или параграфа. Ученики должны быстро с помощью оглавления найти данный раздел учебника и зачитать несколько строк из него. Во время игры развиваются внимательность, быстрота реакции, ориентация в логическом изложении математического материала в учебнике. Основной прием, который учитель может использовать на этом этапе работы с книгой – это прием «Банк идей (гипотез)», куда ученики «складывают» свои мысли о том, что будет сегодня на уроке изучаться. Этот прием научит учеников выдвигать гипотезы исследования и определять, доказаны они или опровергнуты, что очень важно для формирования навыков научно – исследовательской деятельности учащихся при работе с литературой. Прием «Верные или неверные утверждения», или «Верите ли Вы?» может быть началом урока, когда учащиеся, выбирая «верные утверждения» из предложенных учителем, описывают заданную тему. В начале изучения темы «Углы» в 5 классе можно предложить учащимся поиграть в игру «Верю - не верю»:
После знакомства с основной информацией (текст параграфа, лекция по данной теме) мы возвращаемся к данным утверждениям и просим детей оценить их достоверность, используя полученную на уроке информацию. 2 этап – Работа с текстом учебника непосредственно. Это само чтение. Тут необходимо подчеркнуть, что работа с учебником должна обязательно преследовать определенную цель, которую ученикам сначала сообщает учитель, а в последствии они сами начнут ставить перед собой цели чтения учебника, параграфа, главы. Основными целями чтения параграфа учебника могут быть: знакомство с информацией, заложенной в выбранном фрагменте текста, понимание информации, запоминание, использование информации в различных учебных и жизненных ситуациях, подтверждение изученного или того, что знали ранее, отыскание примеров, подтверждение научных фактов, работа с иллюстрациями (рисунками, чертежами, диаграммами). В зависимости от поставленной цели учитель должен организовать чтение параграфа одним из способов (опережающее чтение, углубленное чтение, выборочное чтение, чтение-сканирование, чтение вслух, чтение про себя, чтение по ролям, чтение-изучение, выборочное чтение, просмотр). Для лучшего понимания прочитанного текста учебника можно использовать методический прием – «Инсерт». Технически он достаточно прост. Учащихся надо познакомить с рядом маркировочных знаков и предложить им по мере чтения ставить их карандашом на полях специально подобранного и распечатанного текста. Помечать следует отдельные абзацы или предложения в тексте. Пометки могут быть следующие:
Для учащихся наиболее приемлемым вариантом завершения данной работы с текстом является устное обсуждение или заполнение таблицы. Обычно школьники без труда отмечают, что известное им встретилось в прочитанном тексте, сообщают, что нового и неожиданного для себя они узнали. При этом важно, чтобы ученики прямо зачитывали текст, ссылались на него. Весьма интересным в этом приеме является знак «вопрос». Авторы учебников ставят перед учащимися самые разные вопросы, учитель на уроке требует ответов на них, а вот места для вопросов самих детей ни в учебниках, ни на уроках нет. А результат всего этого хорошо известен: школьники не всегда умеют задавать вопросы, а со временем у них вообще появляется боязнь их задавать. Это стимулирует учащихся к поиску ответа на вопрос, обращению к разным источникам информации. Проведя на уроке объяснение нового материала, выполнив упражнения на закрепление, можно предложить учащимся прочитать параграф, выделить главные мысли, найти в тексте то, о чём я вообще не говорила на уроке. Например, при изучении темы «Умножение натуральных чисел и его свойства» можно опустить в объяснении, когда можно не ставить знак умножения. Учащимся дается задание: найти в тексте то, что не упоминалось на уроке. После ответа на вопрос, предлагается задание: «Определите, какие из равенств верные?» 5∙a = 5a 5+b = 5b (x+4)∙(y-5) = (x+4)(y-5) 6∙8∙n = 48n x∙(2+c) = x(2+c) 7∙2+k = 14k (ab)∙c = abc Проработав канву доказательства теоремы, учитель может выдать каждому ученику карточку, на которой доказательство этой теоремы представлено в виде таблицы, состоящей из двух колонок, одна из которых содержит утверждения, другая – их обоснования, а также имеются пропуски в той или иной колонке. Такие карточки можно делать дифференцированными, изменив количество пропусков. Учащимся необходимо заполнить пустые места в доказательстве. Слабым учащимся можно предложить заполнение этой таблицы с использованием учебника.
Еще одним не простым, но в то же время необходимым способом обработки информации из книги является составление плана прочитанного. Удачно составленный план говорит о конечном итоге, об умении анализировать текст, о степени усвоения содержания. По плану ученикам будет легко восстановить в памяти содержание прочитанного. План ускоряет проработку текста и помогает учащимся 10-11 классов готовиться к зачетам. Важным из способов записи прочитанного, особенно для старших классов, является конспектирование. Конспектирование математических книг занятие трудное и занимательное. Зная, что существует алгебраический язык, который позволяет сокращать обычную запись теоремы, решения примеров, под конспектированием учебника математики мы понимаем перевод обычной записи (на естественном русском языке) в математическую запись (на формальном языке). Учащимся на данном этапе можно предложить заполнить таблицу, в которой данный математический факт необходимо представить с помощью слов, на языке символов и в графическом виде.
Еще одним способом обработки информации из текста является составление тезисов. Тезисы – это основные положения текста, которые доказывают, объясняют, поясняют материал в тексте. Если в плане в определенной последовательности даются только названия основных объектов в виде заголовков, то при составлении тезисов в той же самой последовательности даётся само содержание этих объектов. Можно сравнить план и тезисы на примере одного и того же текста из учебника математики для 5 класса «Угол». План. 1. Понятие угла. 2. Равные углы. 3. Развёрнутый угол. 4. Прямой угол. Тезисы. 1. Углом называют фигуру, образованную двумя лучами, выходящими из одной точки. Лучи, образующие угол, называют сторонами угла, а точку, из которой они выходят,- вершиной угла. 2. Если один угол можно наложить на другой так, что они совпадут, то эти углы равны. 3. Два дополнительных друг другу луча образуют развёрнутый угол. Стороны этого угла вместе образуют прямую линию, на которой лежит вершина развёрнутого угла. 4. Прямым углом называют половину развёрнутого угла. 3 этап- Работа после чтения. После чтения параграфа или главы из учебника ученики должны обязательно высказать свое отношение и свои мысли о прочитанном, привести свои примеры. Важно, чтобы ученики смогли сопоставить прочитанное с тем, что уже знали. После изучения на уроке темы даётся задание составить по материалу учебника контрольные вопросы. Каждый пишет свои вопросы на листочках, которые прикрепляются на «дерево знаний» (изображение на листе ватмана). В начале следующего урока ещё раз прочитывается текст учебника, после чего с «дерева знаний» снимаются листочки, вопросы зачитываются, учащиеся отвечают на них. Такая работа развивает самостоятельность мышления, речевые умения и снижает утомляемость. Еще одним приемом является составление маркировочной таблицы «ЗХУ», которая является вариацией вышеописанного метода «Инсерт». Одной из возможных форм контроля эффективности чтения с пометками является составление маркировочной таблицы.
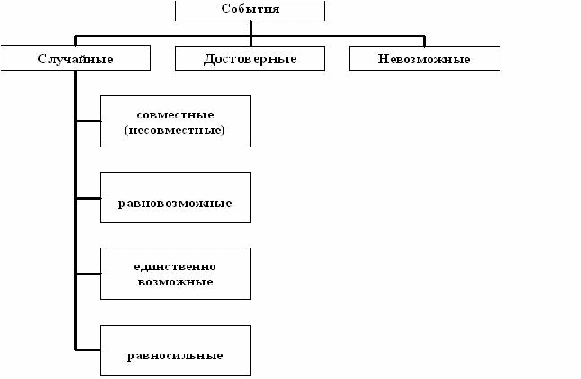
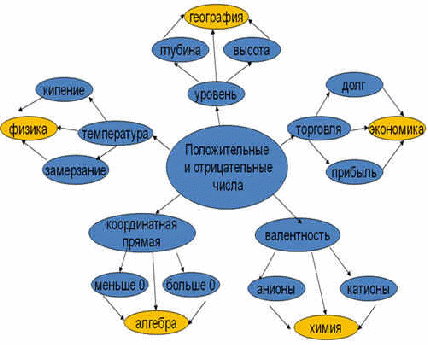
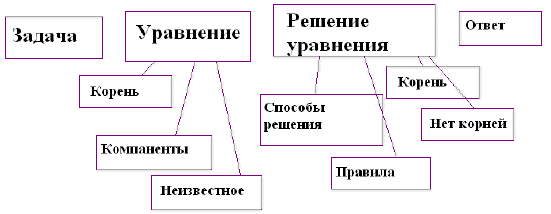
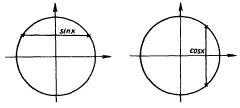
В каждую из колонок необходимо разнести полученную в ходе чтения информацию. Особое требование – записывать сведения, понятия или факты следует только своими словами, не цитируя учебник или иной текст, с которым работали. Прием “ Концептуальная таблица” позволяет учителю проконтролировать работу каждого ученика с текстом учебника и поставить отметку за работу на уроке. Если позволяет время, таблица заполняется прямо на уроке, а если нет, то можно предложить завершить ее дома, а на данном уроке записать в каждой колонке один - два тезиса или положения. Текст учебника математики отличается от других учебников еще и тем, что он насыщен формулировками. Дети с большим трудом запоминают формулировки теорем, правил и алгоритмов выполнения того или иного действия, они их не учат дословно, упуская порой важные слова или искажая смысл. Из-за этого у ребенка возникает неверное ощущение, что он все выучил хорошо, верно привел формулировку, и, как результат, обида на учителя, который снизил оценку. Для заучивания формул и правил важно научить школьников пользоваться мнемоническими правилами. Мнемоника - искусство запоминания - помогает выучить громоздкие формулы или правила, переводя их на язык смешных ассоциаций, созвучных фраз или стихов. Мнемонических правил много. 1. Римские цифры. М=1000,Д=500,С=100,L=50,X=10,V=5,I=1 Мы Дарим Сочные Лимоны, Хватит Всем И ещё останется. 2.Знаки тригонометрических функций.Все тригонометрические функции в 1 четверти принимают положительные значения (знак«+»).Учащиеся легко запоминают, что у тангенса и котангенса знаки располагаются крест-накрест. Для синуса и косинуса – следующее правило: при произнесении слова «синус» ударная гласная «и» вытягивает рот в направлении «↔», значит, у синуса знаки расположены горизонтально. Аналогично, при произнесении слова «косинус», ударная гласная «о» вытягивает рот в направлении «↕», значит, у косинуса знаки расположены вертикально. 3.При решении простейших тригонометрических уравнений sinx = a, cosx=a ребята забывают, какую хорду и в каком случае нужно рассматривать. Опять поможет произнесение слов «синус» и «косинус». Ударная гласная «и» вытягивает рот в направлении «↔», значит на круге при решении уравнения sinx = a надо провести горизонтальную хорду, ударная «о» вытягивает рот в направлении «↕», значит при решении уравнений вида cosx=a будем проводить вертикальную хорду. 4. В формулах приведения можно спросить у ослика: «Надо ли менять название функции на кофункцию?» Если угол а прилежит к вертикальному диаметру (90° a), (270° a), то ослик будет кивать вдоль вертикальной оси и отвечать «да», а если угол а прилежит к горизонтальному диаметру, то ослик поворачивает голову слева направо и отвечает «нет». Вторая часть правила требует определить знак первоначальной функции от сложного аргумента. Еще одно шуточное правило для запоминания формул приведения: Если ГО, то О, Если ВЕ, то МЕ. Если ось ГОризонтальная, то функция Остаётся неизменной, например: sin (π+x) = -sin (x). Если ось ВЕртикальная, то функция МЕняется на кофункцию, например: tg (3π/2-x) = ctg (x). (Необходимо также определить знак приведенной функции) 5. Производные синуса и косинуса. Производная синуса — косинус, производная косинуса — минус синус. Для запоминания этого факта предлагается отождествить синус со словом «синий», а косинус — со словом «косяк». В словосочетании «синий косяк» нет тире, поэтому производная синуса — косинус. В предложении «косяк — синий» есть тире, поэтому производная косинуса — минус синус. По плану, тезисам, конспекту, составленным на втором этапе, ученики должны неоднократно воспроизвести прочитанный материал. После прочтения, обработки текста и ведения записей ученики должны перейти к обобщению. Предлагаем обобщение прочитанного текста осуществить в виде схем, таблиц и рисунков. Приведем в виде примера способ обобщения материала, прочитанного в книге. После изучения темы «Целые числа» учениками могут быть составлены следующие схемы – кластеры (дендрограммы) Кластеры (в переводе означает пучок, созвездие) – выделение смысловых единиц текста и графическое оформление в определенном порядке. Составление кластера позволяет учащимся свободно и открыто думать по поводу какой-либо темы. Ученик записывает в центре листа ключевое понятие, а от него рисует в разные стороны стрелки-лучи, которые соединяют слово с другими, от которых в свою очередь лучи расходятся далее и далее. Кластер может быть использован на самых разных стадиях урока. Например, этот прием может быть применен в стадии вызова, когда мы систематизируем информацию до знакомства с основным источником (текстом) в виде вопросов или заголовков смысловых блоков. Большой потенциал имеет этот прием и на стадии рефлексии: это исправления неверных предположений, заполнение на основе новой информации, установление причинно-следственных связей между отдельными смысловыми блоками. В качестве инструмента для синтезирования сложной информации, а учителю – в качестве среза оценки понятийного и словарного багажа учащихся можно предложить составить синквейн. Слово «синквейн» происходит от французского «пять». Это стихотворение из пяти строк,
Таким образом, эффективность процесса обучения зависит от умения правильно выбрать технологические приёмы, удачно комбинировать их, вмещать их в рамки уже знакомых традиционных форм урока. Важно понимать, что каждый ученик успешен, талантлив и уникален во всем. Технология критического мышления позволяет определить сферу комфортности для каждого. Кроме того, при переходе с одного приема на другой меняется режим работы мозга. А это позволяет предупреждать утомляемость и приводит к развитию когнитивных способностей. Использование данной стратегии ориентировано на развитие навыков вдумчивой работы с любой информацией, а не только с текстом. Учебник является важнейшим источником вопросов, задач и заданий, которые учитель ставит перед учащимися или которые они находят самостоятельно. Научить школьника приёмам работы с учебником, с книгой – это значит научить его учиться. Важно научить ученика самостоятельно работать с книгой, вырабатывать умения и навыки осмысленного чтения и осознанного усвоения изложенного в ней материала. Рассмотренные приёмы работы с текстом учебника обеспечивают не только усвоение учебного материала, но и активизирует умственную деятельность учащихся, прививает интерес к изучаемому предмету. Литература: 1. Н. Н .Сметанникова. Обучение стратегиям чтения в 5-9 классах: Как реализовать ФГОС. Пособие для учителя/ Н. Н. Сметанникова. – М.: Баласс, 2011 г. 2. https://centeroko.ru/pisa09/pisa09_res.htm 3. Акулова О. В., Писарева С. А., Пискунова Е. В. Конструирование ситуационных задач для оценки компетентности учащихся. – СПб.: КАРО, 2008 г. 4. А. И. Люберанский .Формулы и мнемонические правила. Журнал «Математика в школе» №6, 1999 г., стр. 48 5.И.Б. Гусева, Г. В. Сычёва. Учимся преобразовывать тригонометрические выражения .Журнал «Математика в школе» №10, 2000 г., стр.3 Плотникова Г.В., МКОУ «Сибирская СОШ №1» |