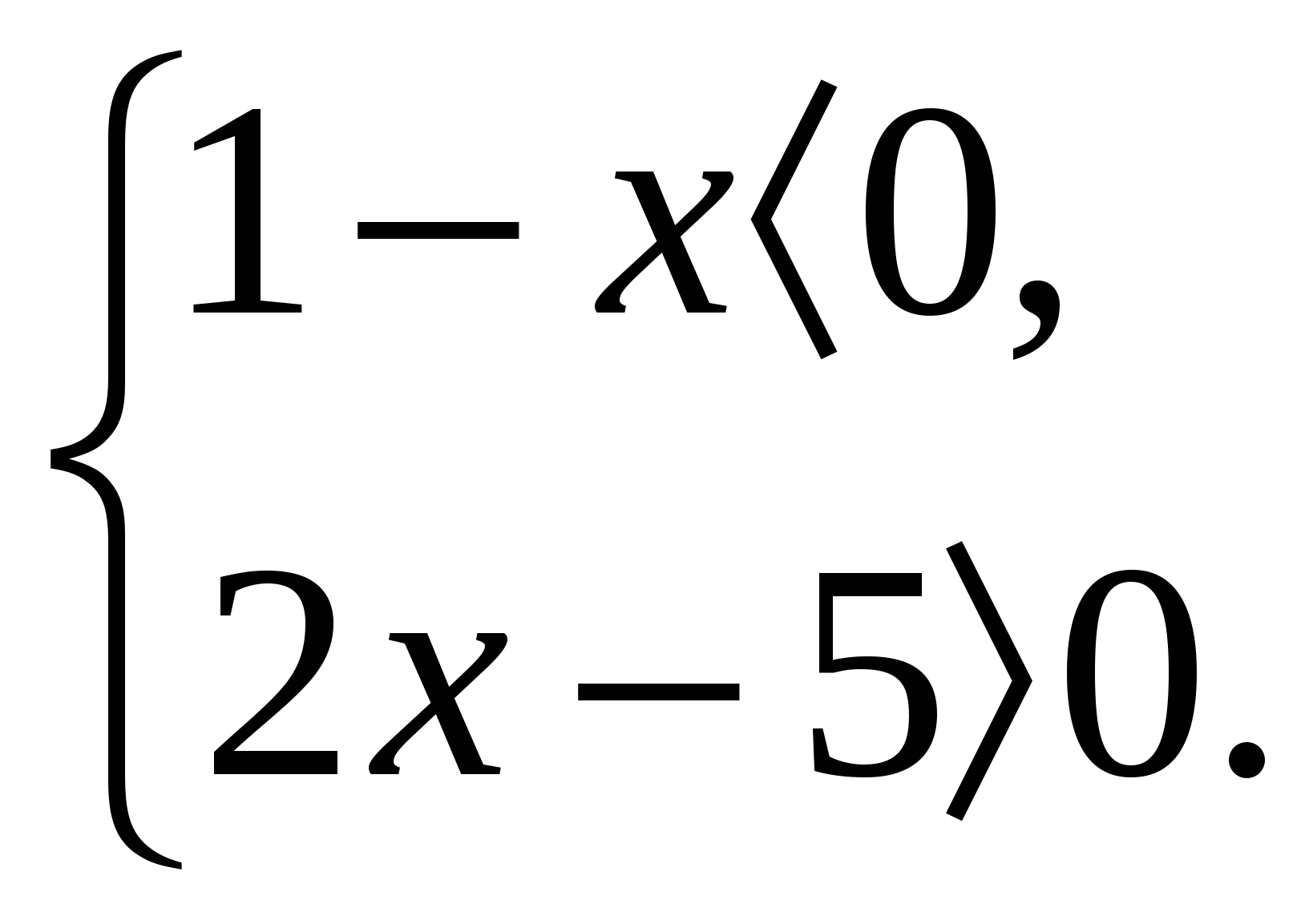|
ТРЕБОВАНИЯ К УРОВНЮ ПОДГОТОВКИ УЧАЩИХСЯ 9 КЛАССА
В результате изучения алгебры выпускник 9 класса должен
знать/понимать
существо понятия математического доказательства; примеры доказательств;
существо понятия алгоритма; примеры алгоритмов;
как используются математические формулы, уравнения и неравенства; примеры их применения для решения математических и практических задач;
как математически определенные функции могут описывать реальные зависимости; приводить примеры такого описания;
как потребности практики привели математическую науку к необходимости расширения понятия числа;
вероятностный характер многих закономерностей окружающего мира; примеры статистических закономерностей и выводов;
смысл идеализации, позволяющей решать задачи реальной действительности математическими методами, примеры ошибок, возникающих при идеализации;
уметь
выполнять устно арифметические действия: сложение и вычитание двузначных чисел и десятичных дробей с двумя знаками, умножение однозначных чисел, арифметические операции с обыкновенными дробями с однозначным знаменателем и числителем;
переходить от одной формы записи чисел к другой, представлять десятичную дробь в виде обыкновенной и в простейших случаях обыкновенную в виде десятичной, проценты — в виде дроби и дробь — в виде процентов; записывать большие и малые числа с использованием целых степеней десятки;
выполнять арифметические действия с рациональными числами, сравнивать рациональные и действительные числа; находить в несложных случаях значения степеней с целыми показателями и корней; находить значения числовых выражений;
округлять целые числа и десятичные дроби, находить приближения чисел с недостатком и с избытком, выполнять оценку числовых выражений;
пользоваться основными единицами длины, массы, времени, скорости, площади, объема; выражать более крупные единицы через более мелкие и наоборот;
решать текстовые задачи, включая задачи, связанные с отношением и с пропорциональностью величин, дробями и процентами;
составлять буквенные выражения и формулы по условиям задач; осуществлять в выражениях и формулах числовые подстановки и выполнять соответствующие вычисления, осуществлять подстановку одного выражения в другое; выражать из формул одну переменную через остальные;
выполнять основные действия со степенями с целыми показателями, с многочленами и с алгебраическими дробями; выполнять разложение многочленов на множители; выполнять тождественные преобразования рациональных выражений;
применять свойства арифметических квадратных корней для вычисления значений и преобразований числовых выражений, содержащих квадратные корни;
решать линейные, квадратные уравнения и рациональные уравнения, сводящиеся к ним, системы двух линейных уравнений и несложные нелинейные системы;
решать линейные и квадратные неравенства с одной переменной и их системы;
решать текстовые задачи алгебраическим методом, интерпретировать полученный результат, проводить отбор решений, исходя из формулировки задачи;
изображать числа точками на координатной прямой;
определять координаты точки плоскости, строить точки с заданными координатами; изображать множество решений линейного неравенства;
распознавать арифметические и геометрические прогрессии; решать задачи с применением формулы общего члена и суммы нескольких первых членов;
находить значения функции, заданной формулой, таблицей, графиком по ее аргументу; находить значение аргумента по значению функции, заданной графиком или таблицей;
определять свойства функции по ее графику; применять графические представления при решении уравнений, систем, неравенств;
описывать свойства изученных функций, строить их графики;
проводить несложные доказательства, получать простейшие следствия из известных или ранее полученных утверждений, оценивать логическую правильность рассуждений, использовать примеры для иллюстрации и контрпримеры для опровержения утверждений;
извлекать информацию, представленную в таблицах, на диаграммах, графиках; составлять таблицы, строить диаграммы и графики;
решать комбинаторные задачи путем систематического перебора возможных вариантов, а также с использованием правила умножения;
вычислять средние значения результатов измерений;
находить частоту события, используя собственные наблюдения и готовые статистические данные;
находить вероятности случайных событий в простейших случаях;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
решения несложных практических расчетных задач, в том числе c использованием при необходимости справочных материалов, калькулятора, компьютера;
устной прикидки и оценки результата вычислений; проверки результата вычисления с использованием различных приемов;
интерпретации результатов решения задач с учетом ограничений, связанных с реальными свойствами рассматриваемых процессов и явлений;
выполнения расчетов по формулам, составления формул, выражающих зависимости между реальными величинами; нахождения нужной формулы в справочных материалах;
моделирования практических ситуаций и исследовании построенных моделей с использованием аппарата алгебры;
описания зависимостей между физическими величинами соответствующими формулами при исследовании несложных практических ситуаций;
интерпретации графиков реальных зависимостей между величинами;
выстраивания аргументации при доказательстве (в форме монолога и диалога);
распознавания логически некорректных рассуждений;
записи математических утверждений, доказательств;
анализа реальных числовых данных, представленных в виде диаграмм, графиков, таблиц;
решения практических задач в повседневной и профессиональной деятельности с использованием действий с числами, процентов, длин, площадей, объемов, времени, скорости;
решения учебных и практических задач, требующих систематического перебора вариантов;
сравнения шансов наступления случайных событий, оценки вероятности случайного события в практических ситуациях, сопоставления модели с реальной ситуацией;
понимания статистических утверждений.
КОНТРОЛЬ РЕАЛИЗАЦИИ ПРОГРАММЫ
Вводный контроль.
Вариант 1
1
|
Найти абсолютную погрешность числа 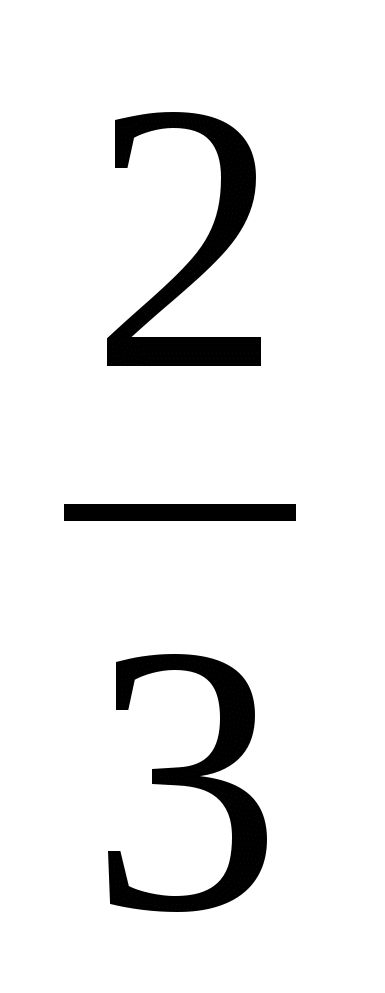 числом 0,7 числом 0,7
|
1) 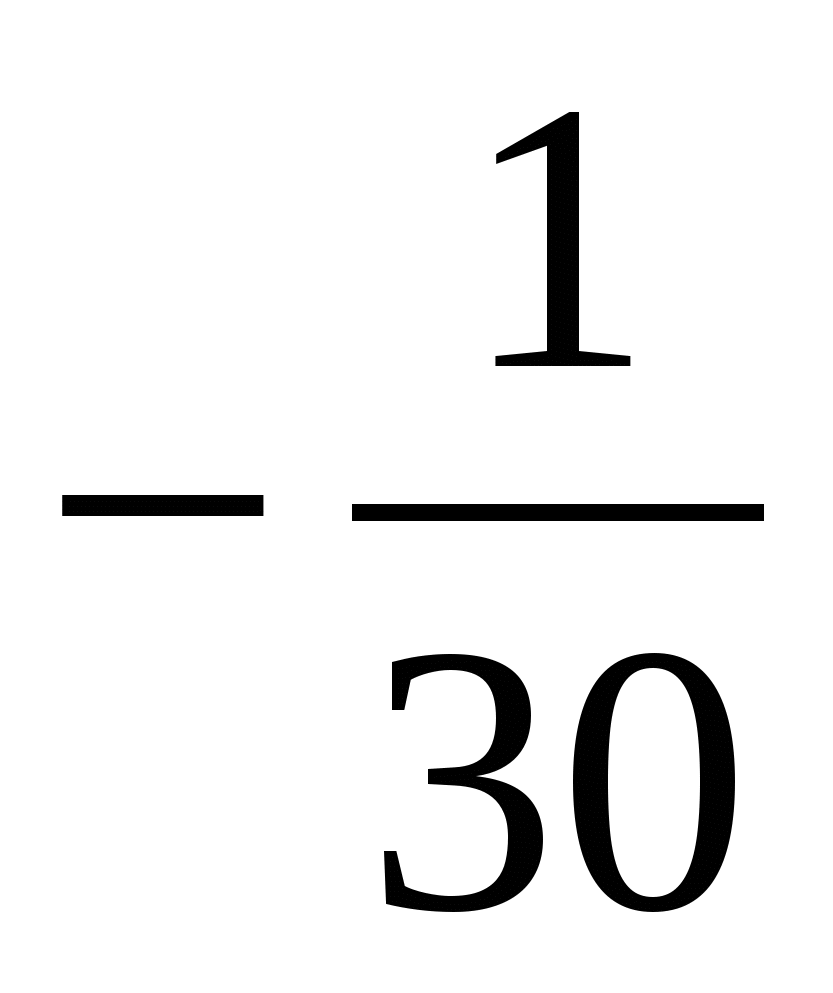
|
2) 0,033
|
3) 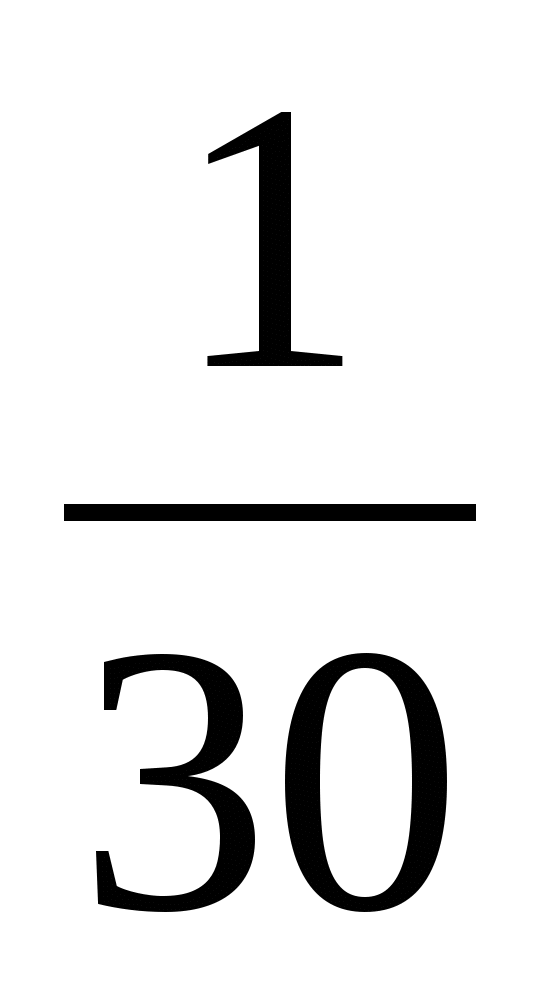
|
4) 0,03
|
2
|
Записать число 420,01 в стандартном виде.
|
1) 4,2001· 102
|
2) 0,42001· 103
|
3) 42001· 10-2
|
4) 420
|
3
|
Сравнить х с нулём, если - ах2 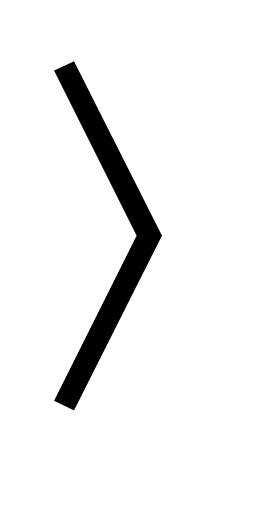 0. 0.
|
1) 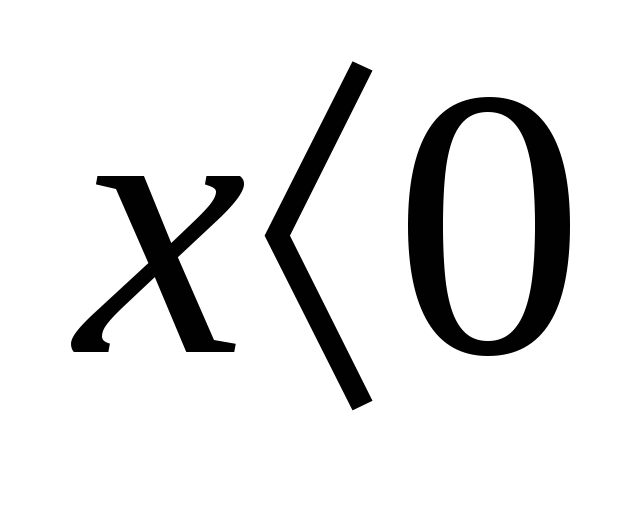
|
2) 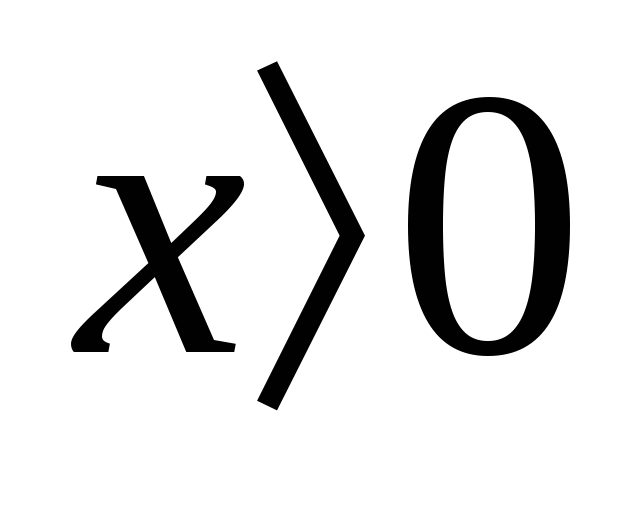
|
3) х=0
|
4) нельзя сравнить
|
4
|
Решить уравнение (х – 1)(х + 3) = 0.
|
1) х1=-1, х2=3
|
1) х1=1, х2=3
|
3) х1=-1, х2=-3
|
4) х1=1, х2=-3
|
5
|
Решить уравнение 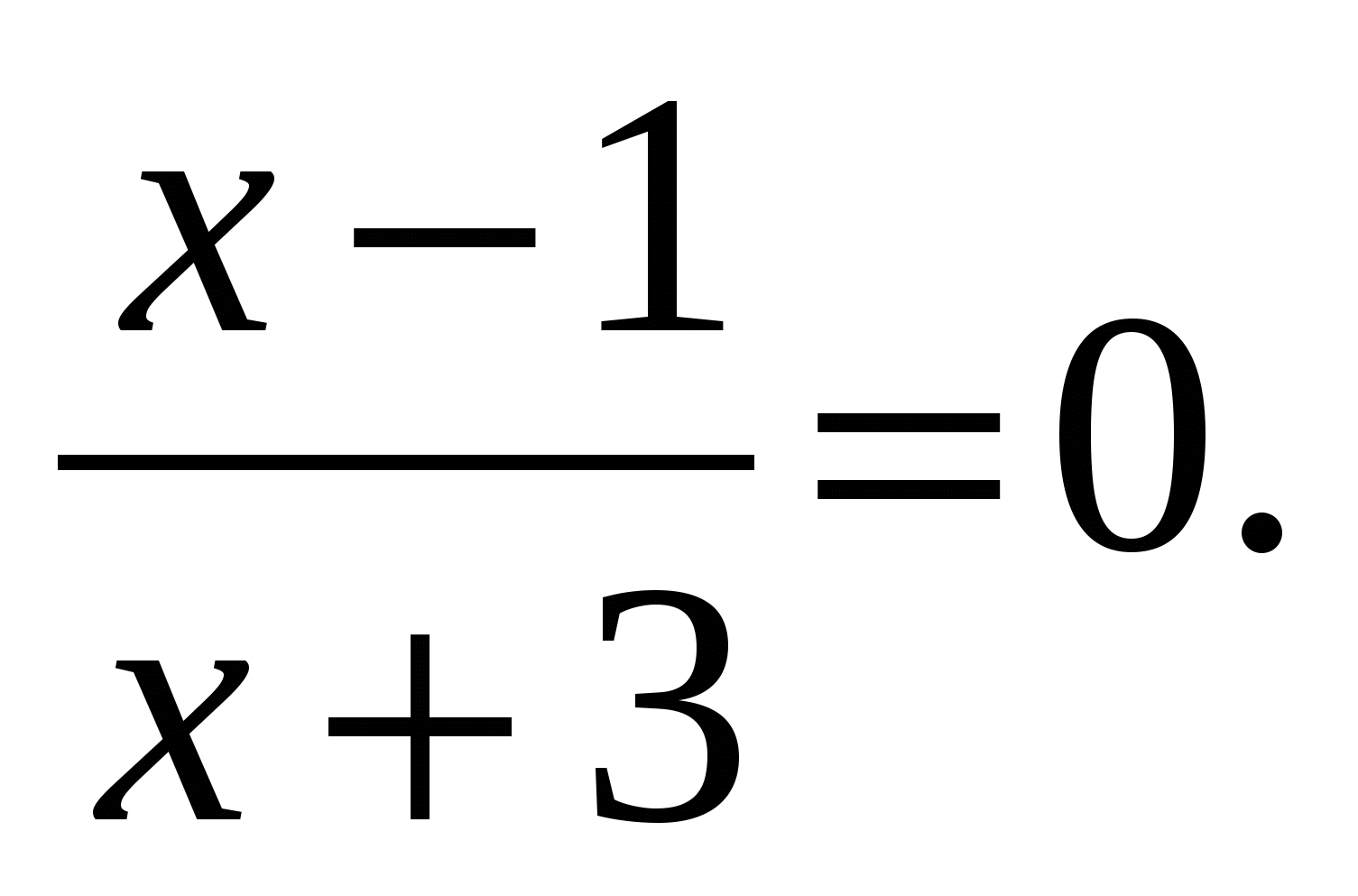
|
1) х=1
|
2) х1=1, х2= - 3
|
3) х = -3
|
4) нет корней
|
6
|
Решить неравенство 2х – 3 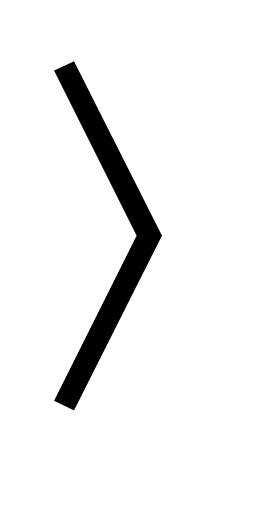 - 5 . - 5 .
|
1) х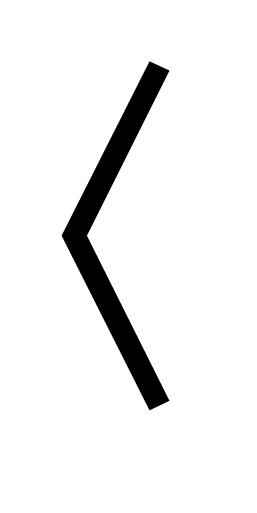 - 1 - 1
|
2) х 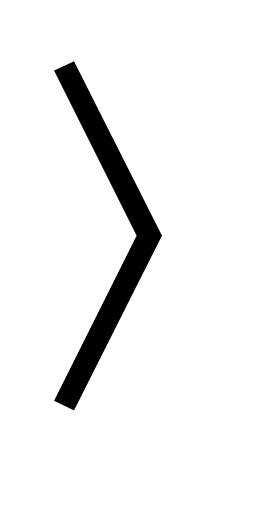 - 8 - 8
|
3) х 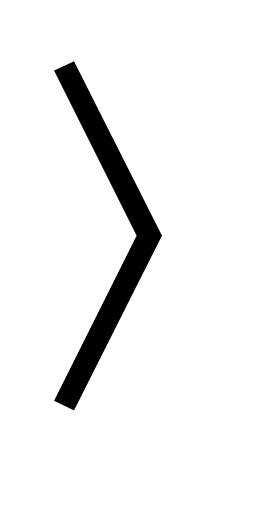 - 4 - 4
|
4) х 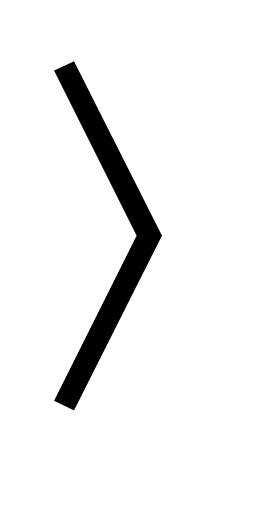 - 1 - 1
|
7
|
Решить неравенство 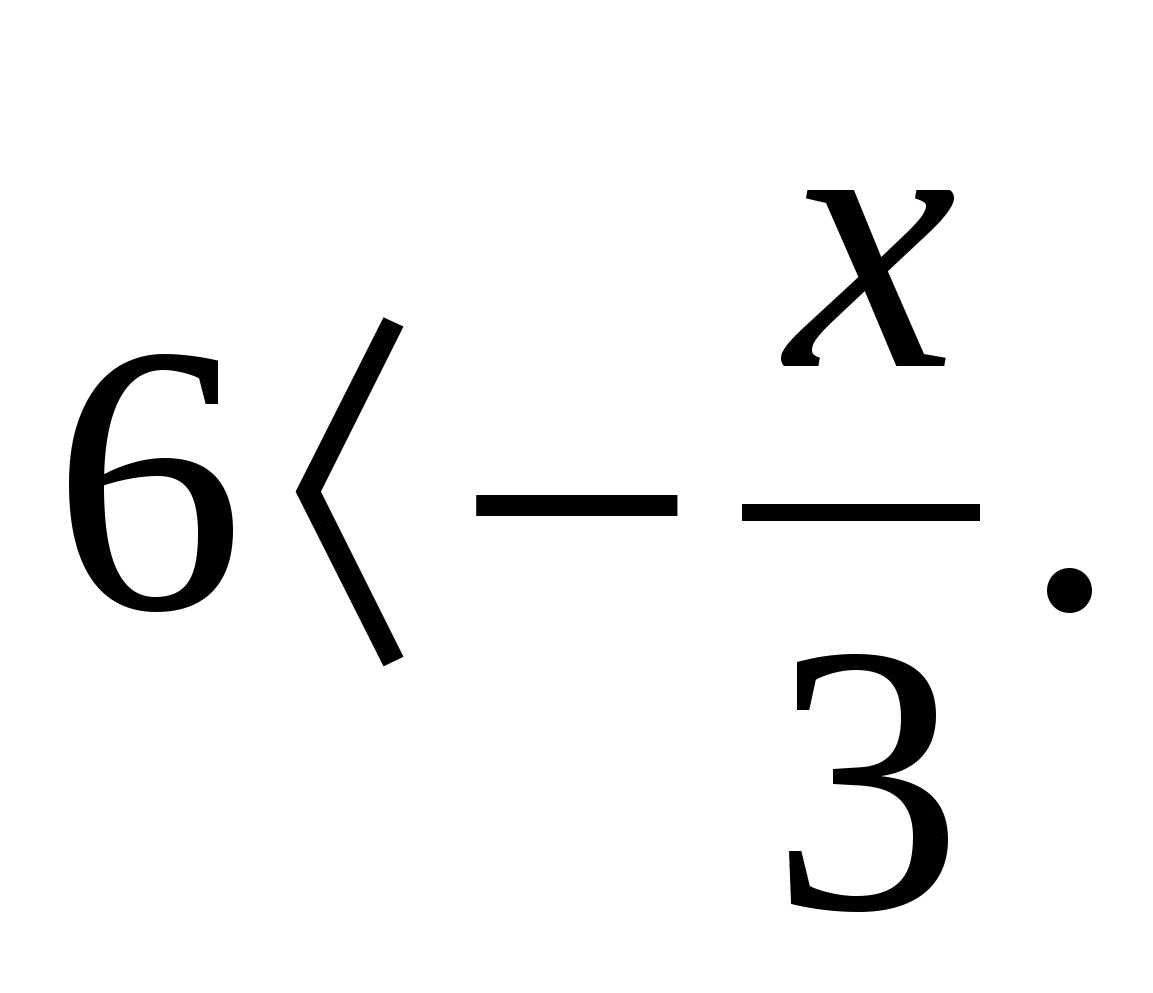
|
1) х 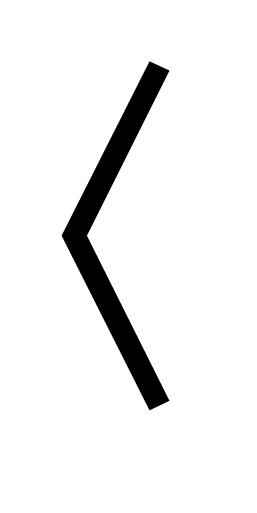 -2 -2
|
2) х 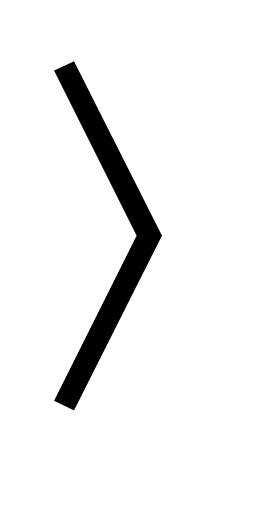 - 2 - 2
|
3) х 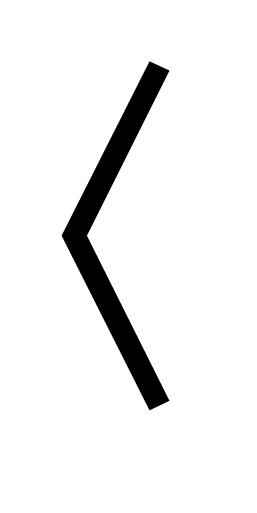 - 18 - 18
|
4) х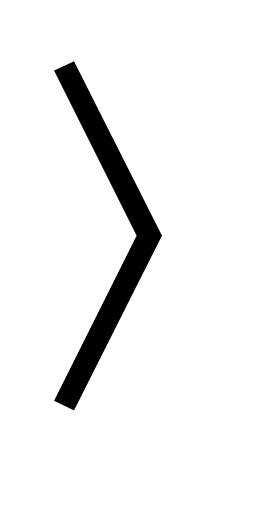 - 18 - 18
|
8
|
Указать наибольшее целое число, являющееся решением неравенства 2х + 7 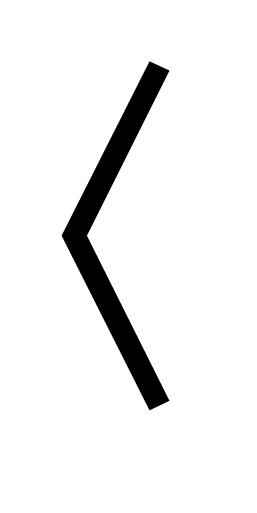 1. 1.
|
1) - 3
|
2) - 4
|
3) - 2
|
4) 0
|
9
|
Решить систему неравенств 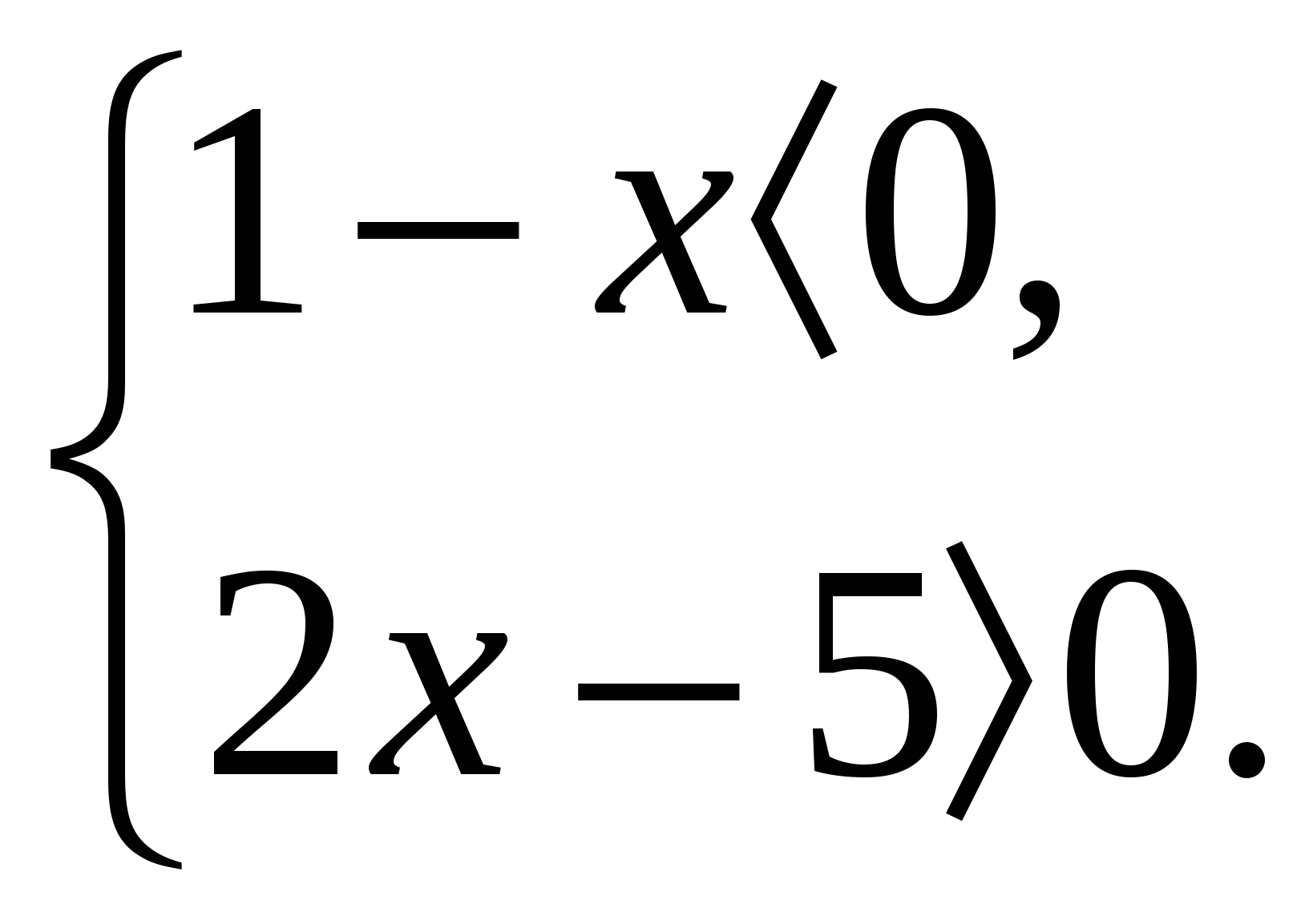
|
1) (2,5; 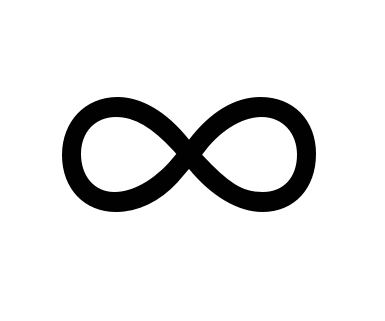 ) )
|
2) (1; 2,5)
|
3) (1; 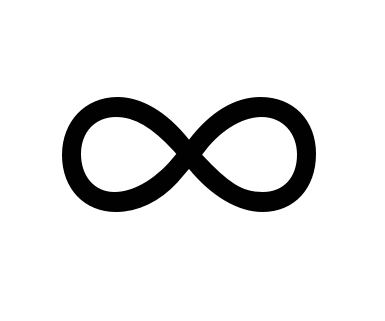 ) )
|
4) решений нет
|
10
|
Сколько целых решений имеет неравенство - 2 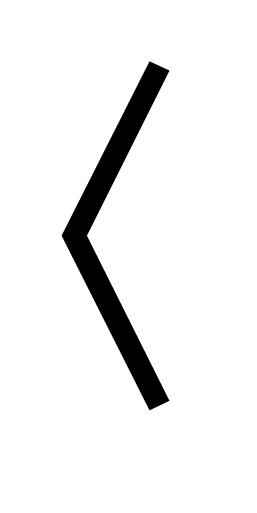 х х 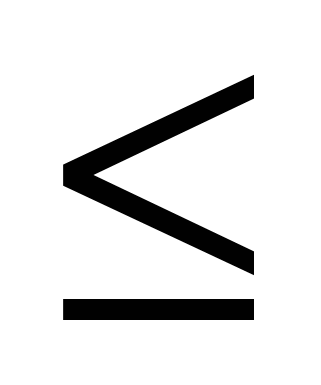 1 ? 1 ?
|
1) 1
|
2) 2
|
3) 3
|
4) 4
|
11
|
Решить уравнение ׀ х׀= 3
|
1) х ≥ 3, х 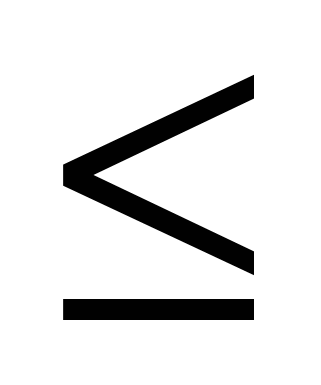 -3 -3
|
2) - 3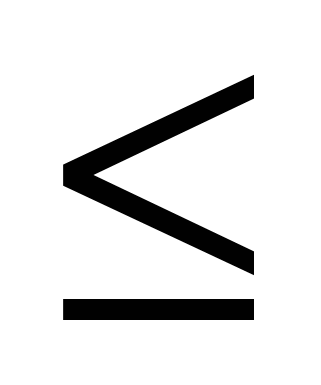 х х 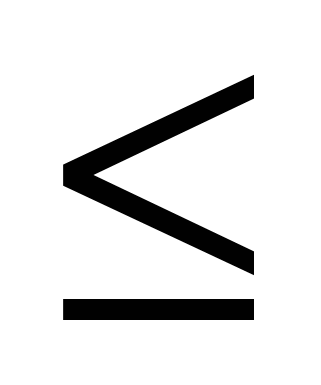 3 3
|
3) х = 3
|
4) х = ± 3
|
12
|
Решить уравнение 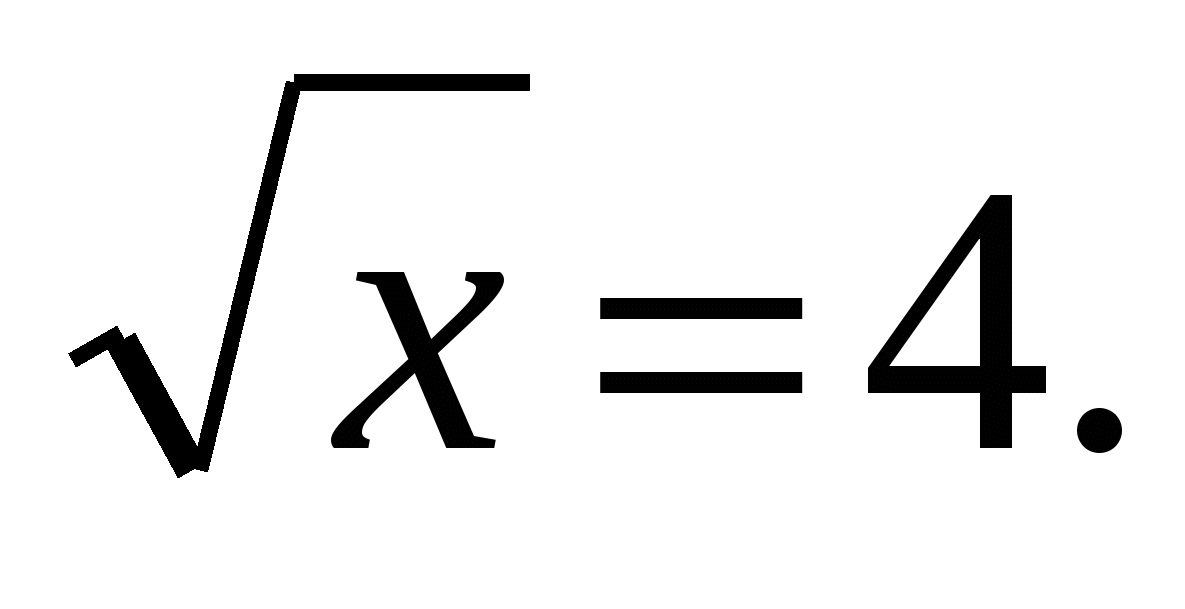
|
1) х = 2
|
2) х = 16
|
3) х = 8
|
4) х = ± 16
|
13
|
Вычислить 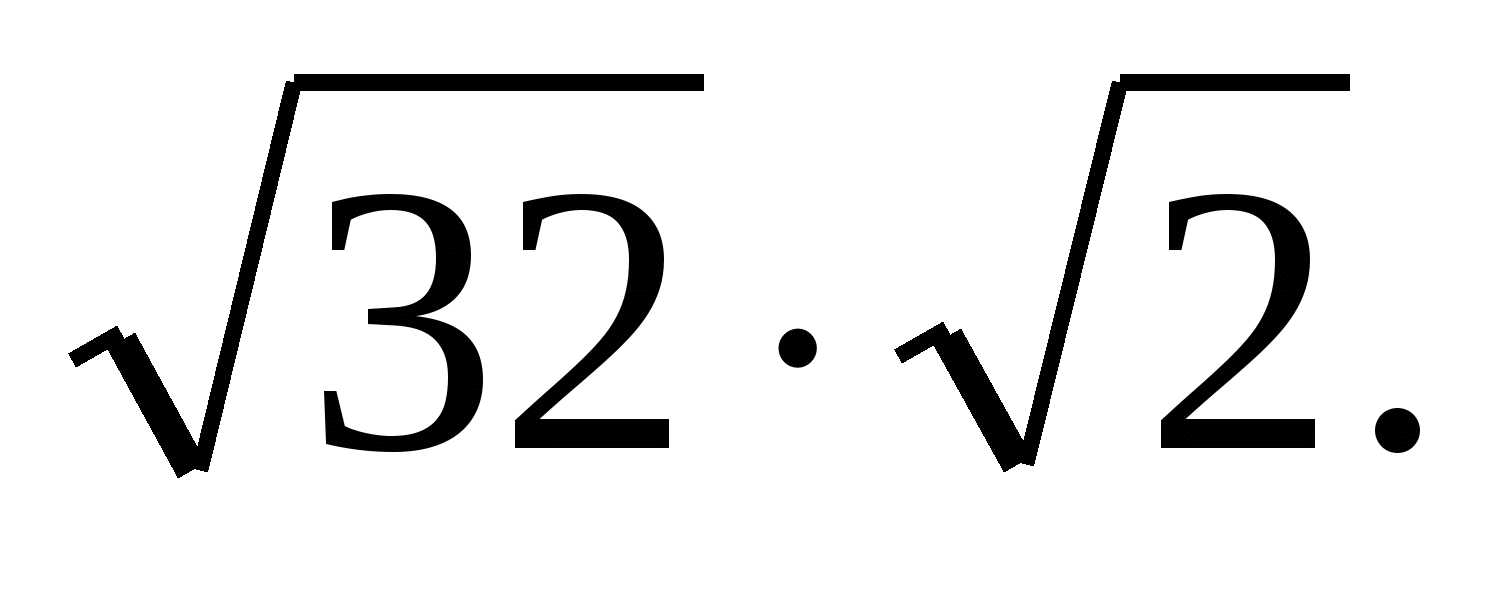
|
1) 4
|
2) 16
|
3) 16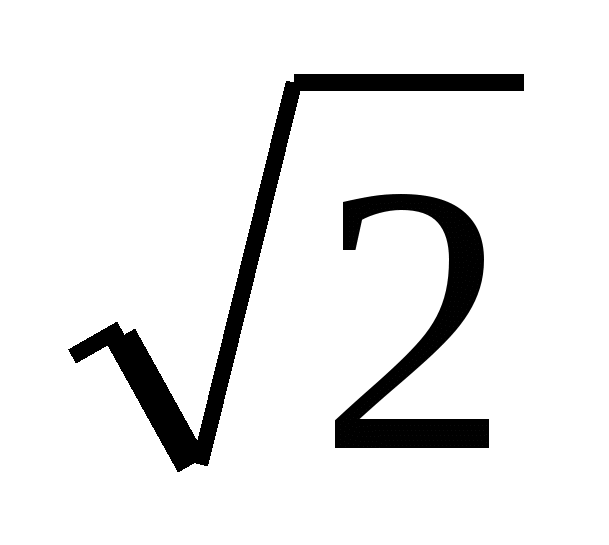
|
4) 8
|
14
|
Вычислить 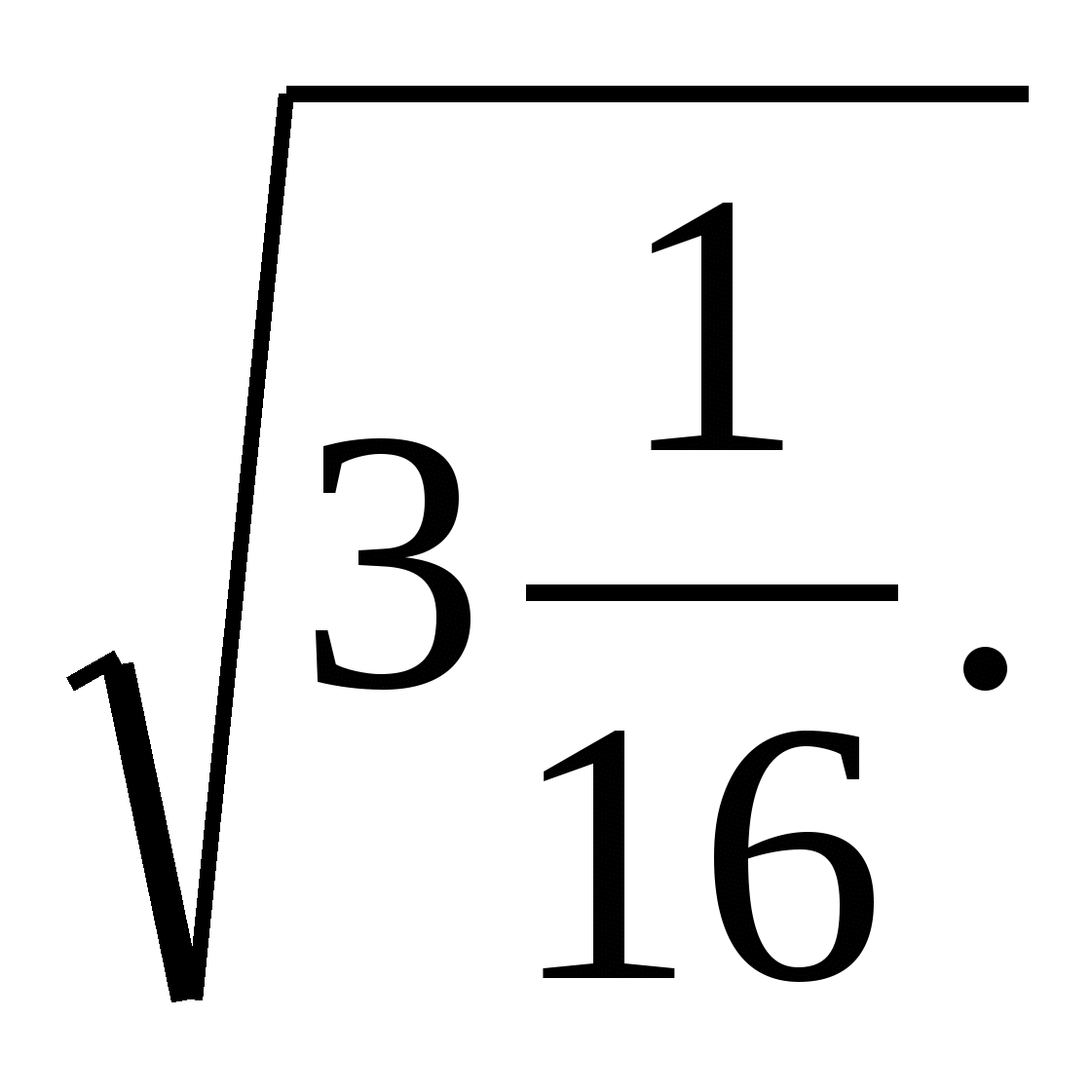
|
1) 1,75
|
2) 3,25
|
3)  
|
4) 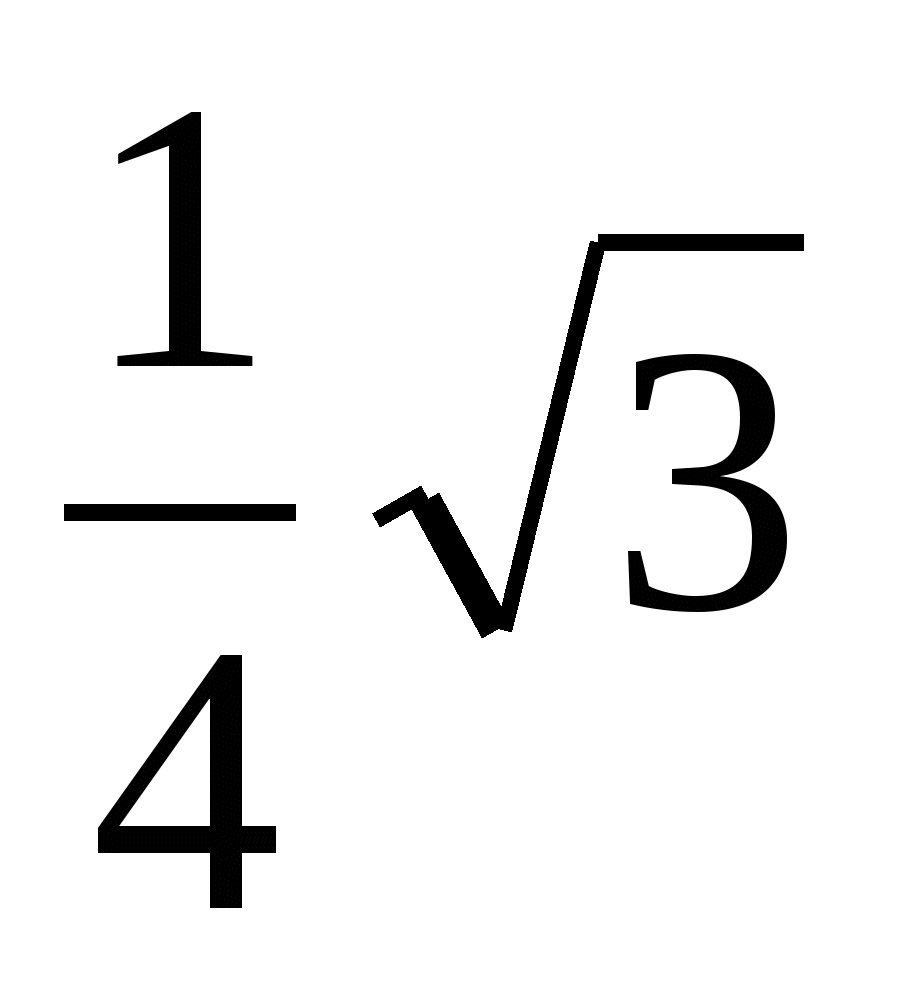
|
15
|
Вынести множитель за знак корня 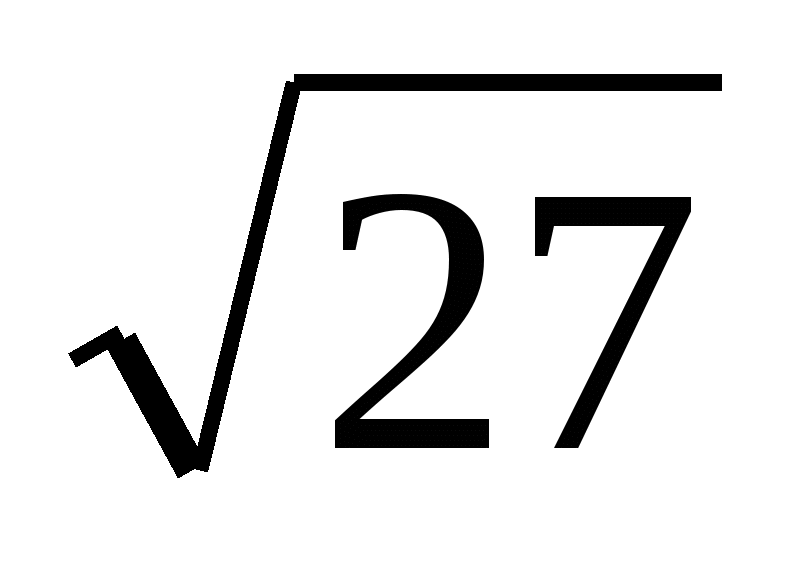 . .
|
1) 3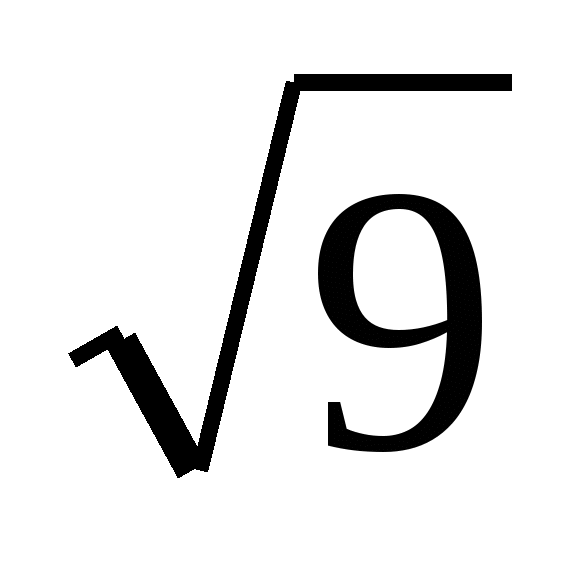
|
2) 9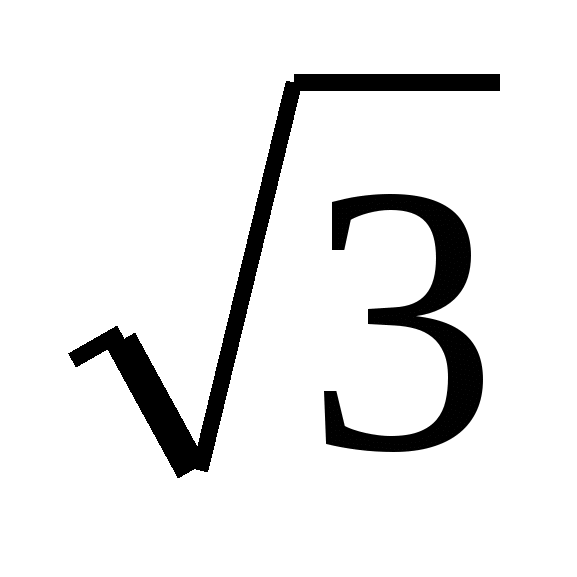
|
3) 3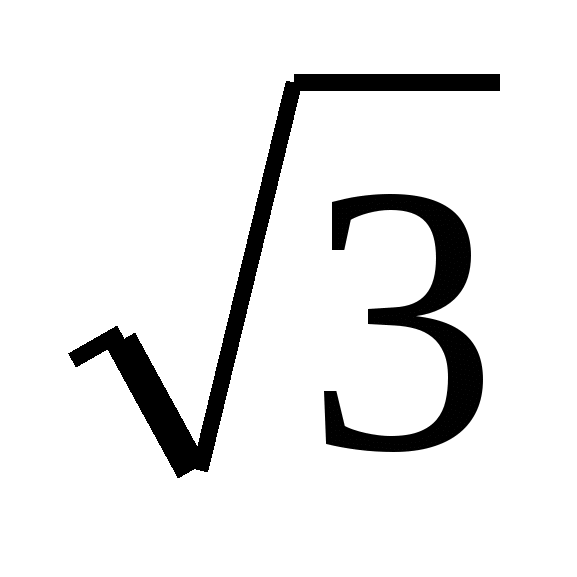
|
4) 3
|
16
|
Внести множитель под знак корня - 3 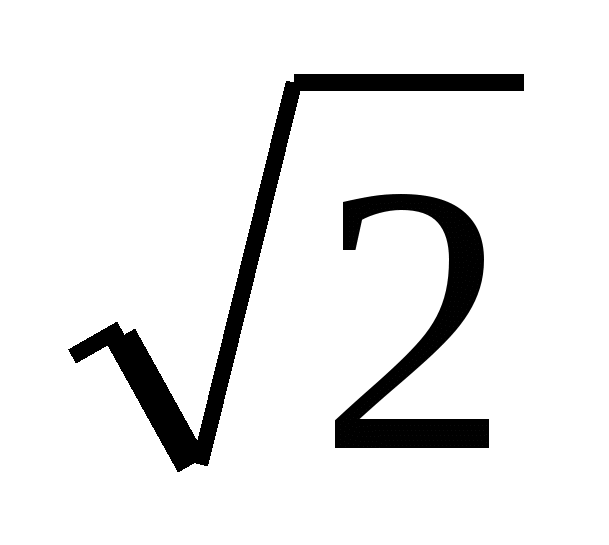
|
1) 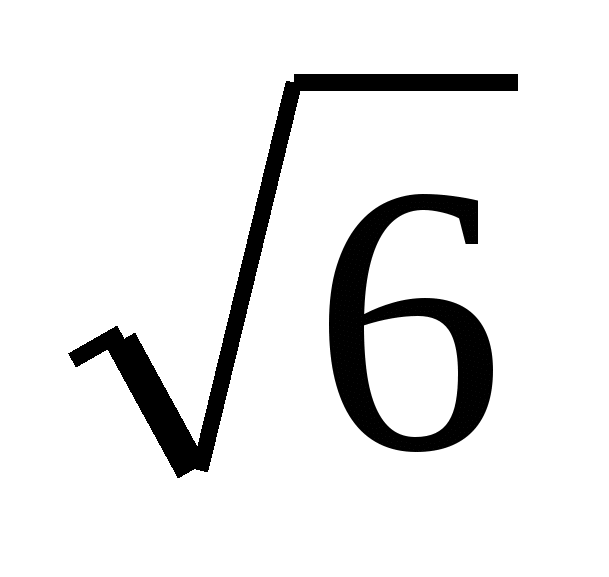
|
2) - 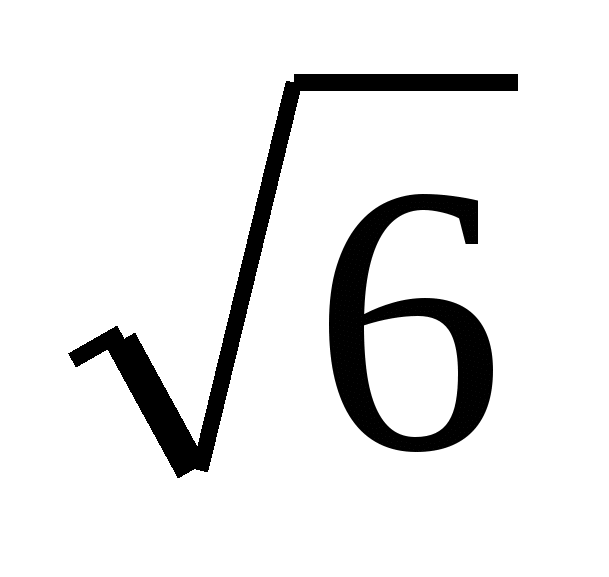
|
3) 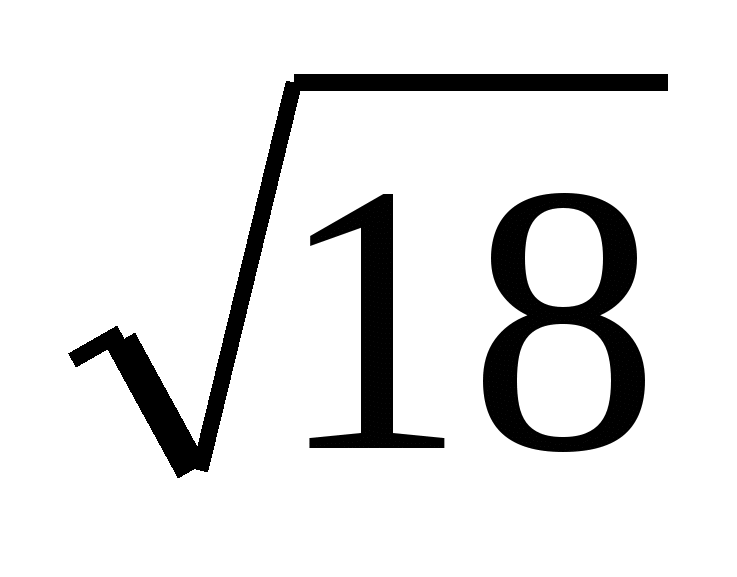
|
4) - 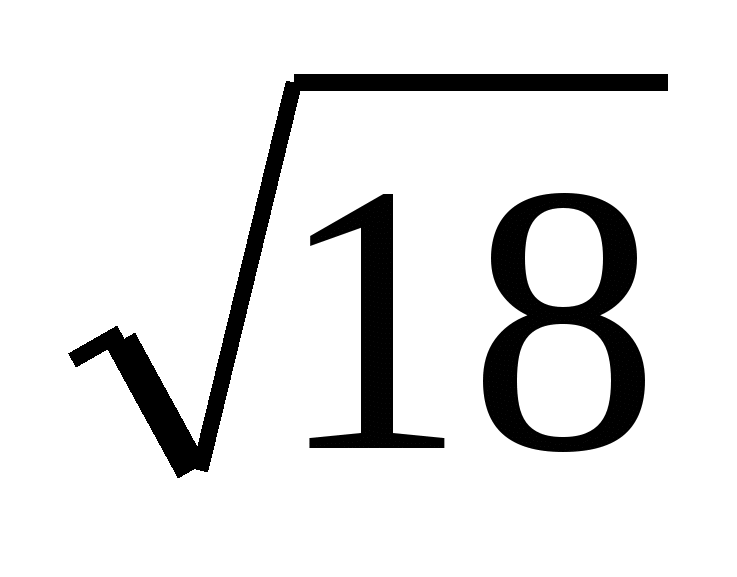
|
17
|
Решить уравнение х2 = 36
|
1) 6
|
2) ± 6
|
3) 18
|
4) ±18
|
18
|
Найти корни уравнения х2 – х = 0.
|
1) ±1; 0
|
2) 1; 0
|
3) – 1; 0
|
4) 0
|
19
|
Решить уравнение 3х2 – 8х – 3 = 0.
|
1) 3; 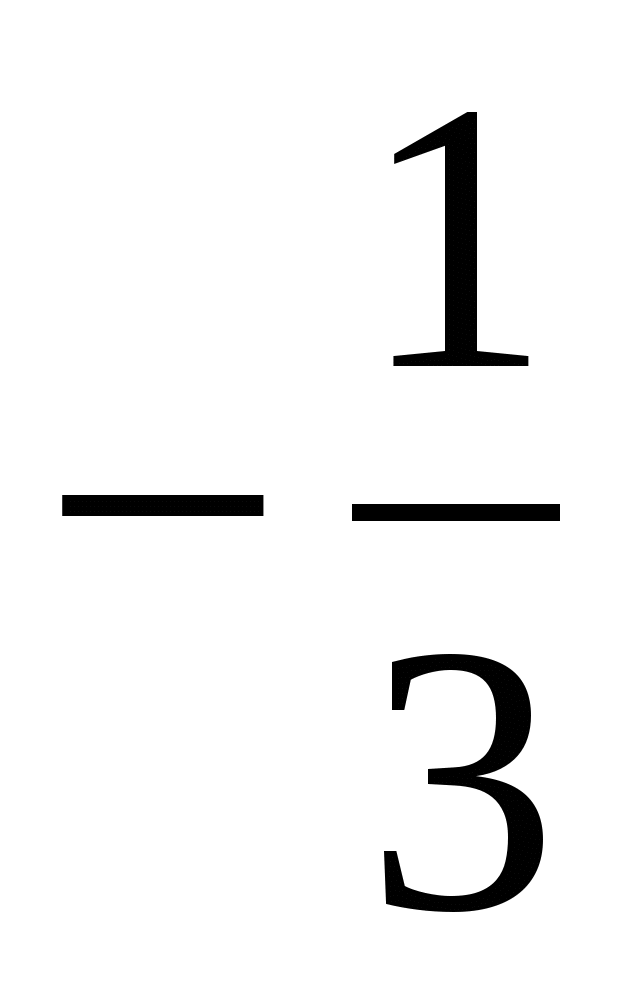
|
2) -3; 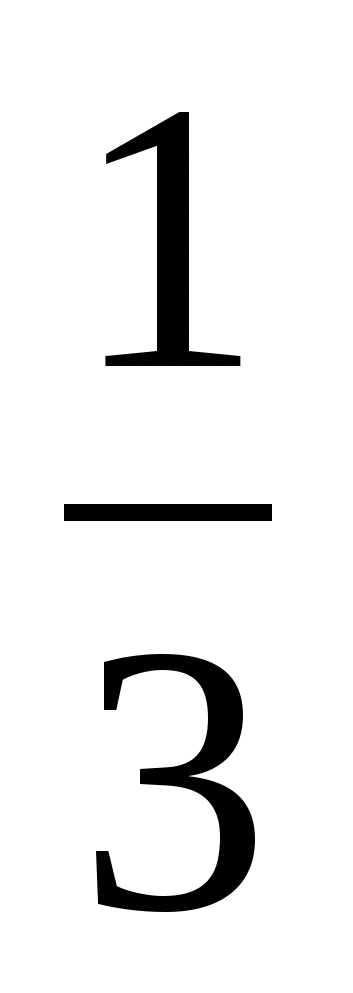
|
3) 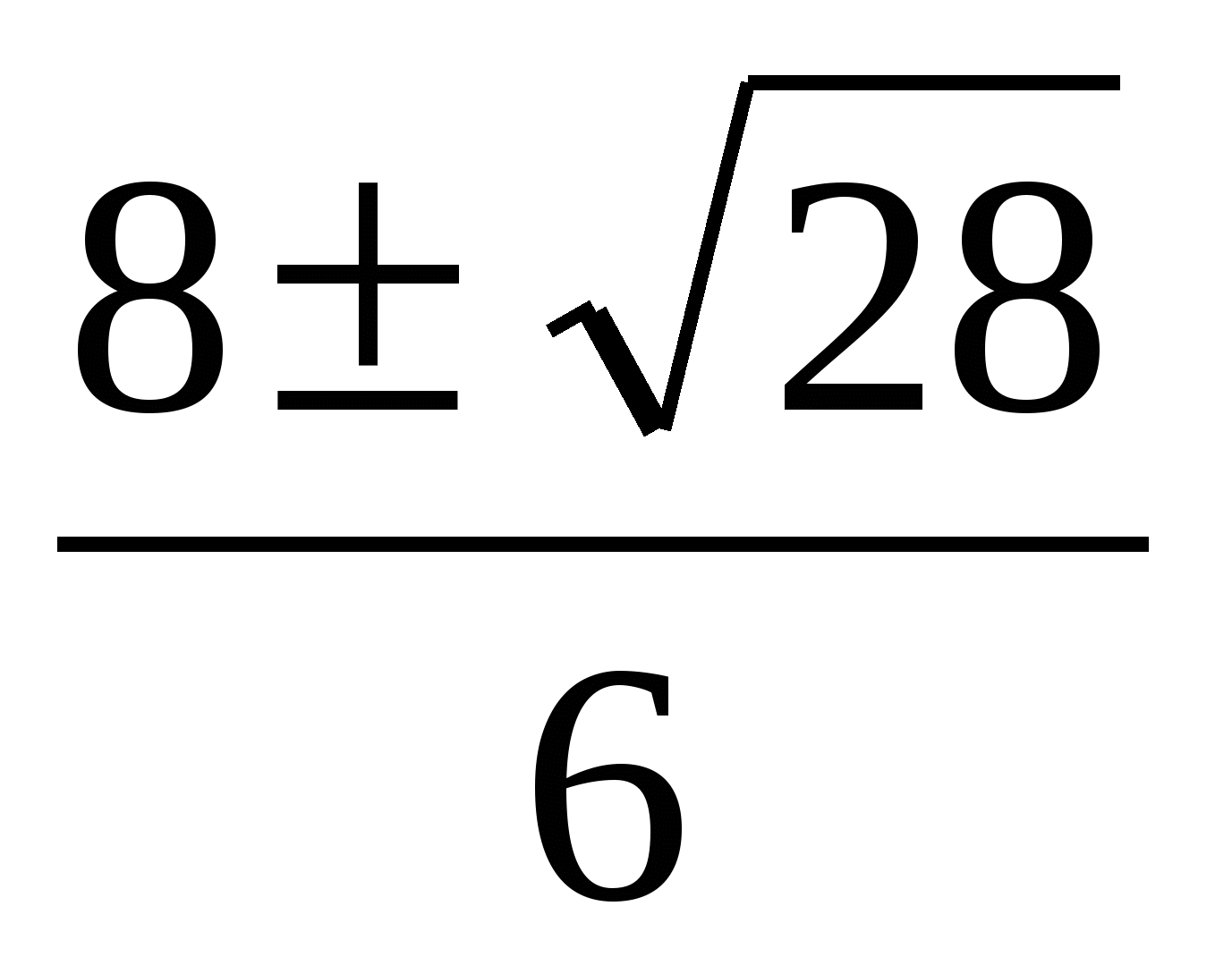
|
4) нет корней
|
20
|
По теореме Виета найти сумму корней уравнения х2 – 5х + 3 = 0
|
1) - 3
|
2) 5
|
3) - 5
|
4) 3
|
Вариант 2
1
|
Найти абсолютную погрешность числа 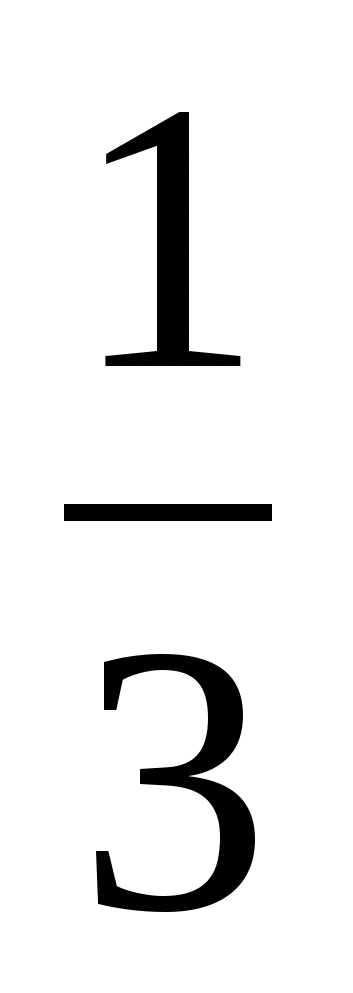 числом 0,3 числом 0,3
|
1) 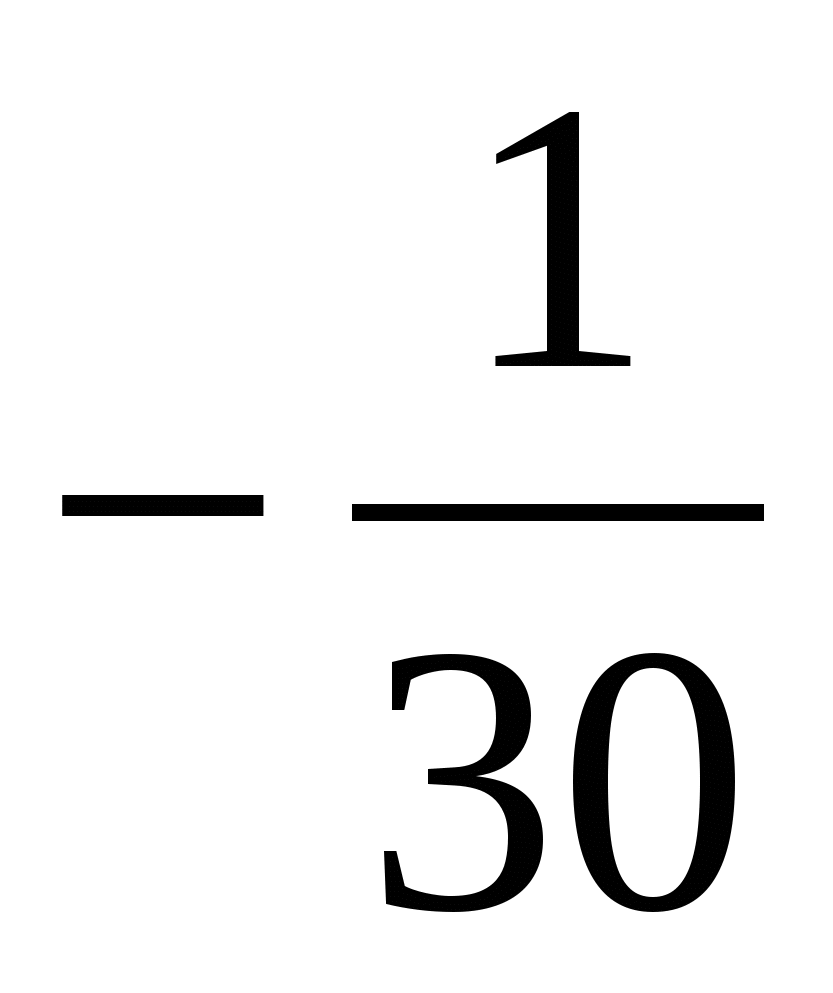
|
2) 0,033
|
3) 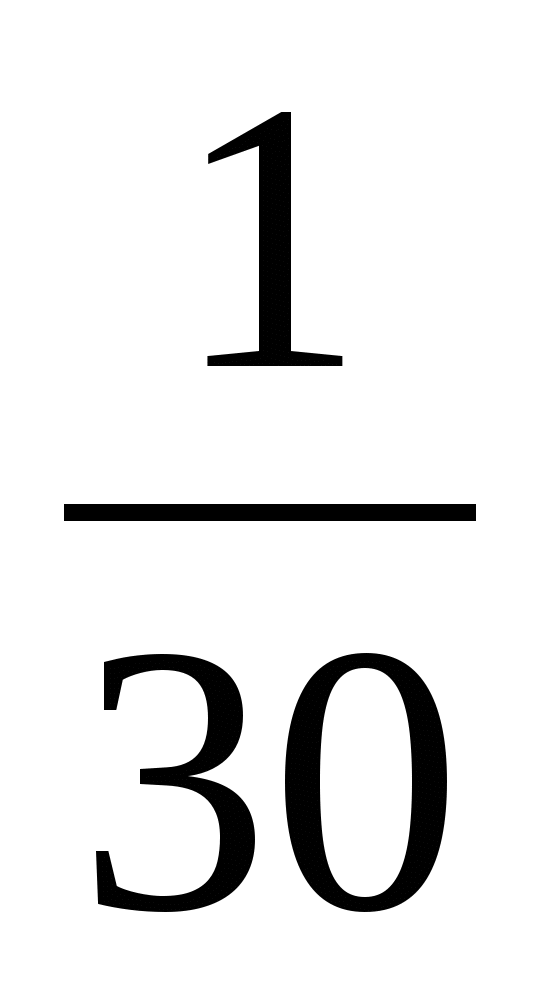
|
4) 0,03
|
2
|
Записать число 564,01 в стандартном виде.
|
1) 5,6401· 102
|
2) 0,56401· 103
|
3) 56401· 10-2
|
4) 564
|
3
|
Сравнить х с нулём, если ах2 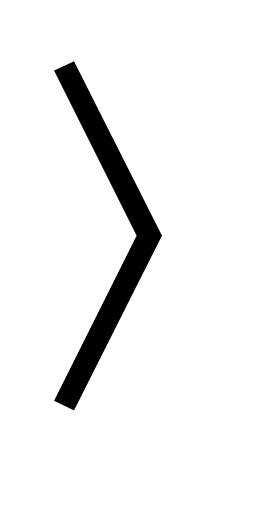 0. 0.
|
1) 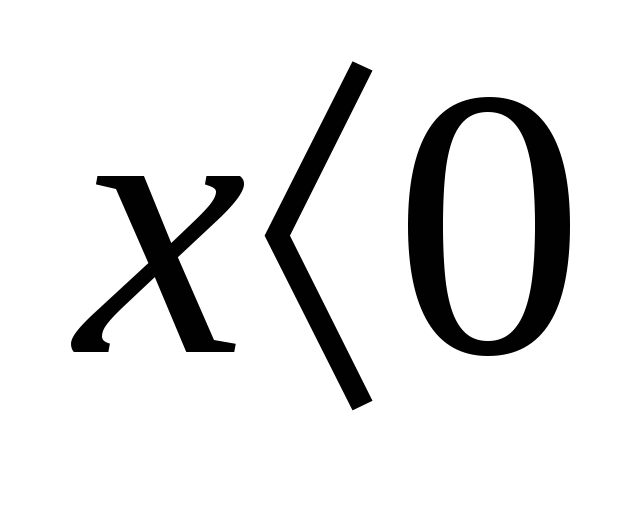
|
2) 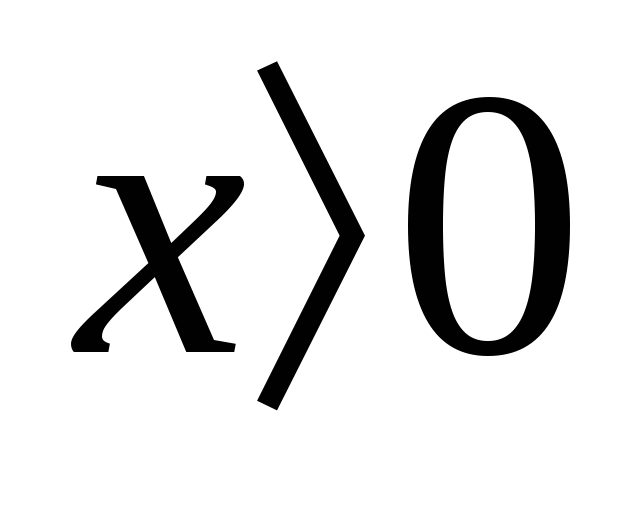
|
3) х=0
|
4) нельзя сравнить
|
4
|
Решить уравнение (х – 1)(х + 3) = 0.
|
1) х1=-1, х2=3
|
1) х1=1, х2=3
|
3) х1=-1, х2=-3
|
4) х1=1, х2=-3
|
5
|
Решить уравнение 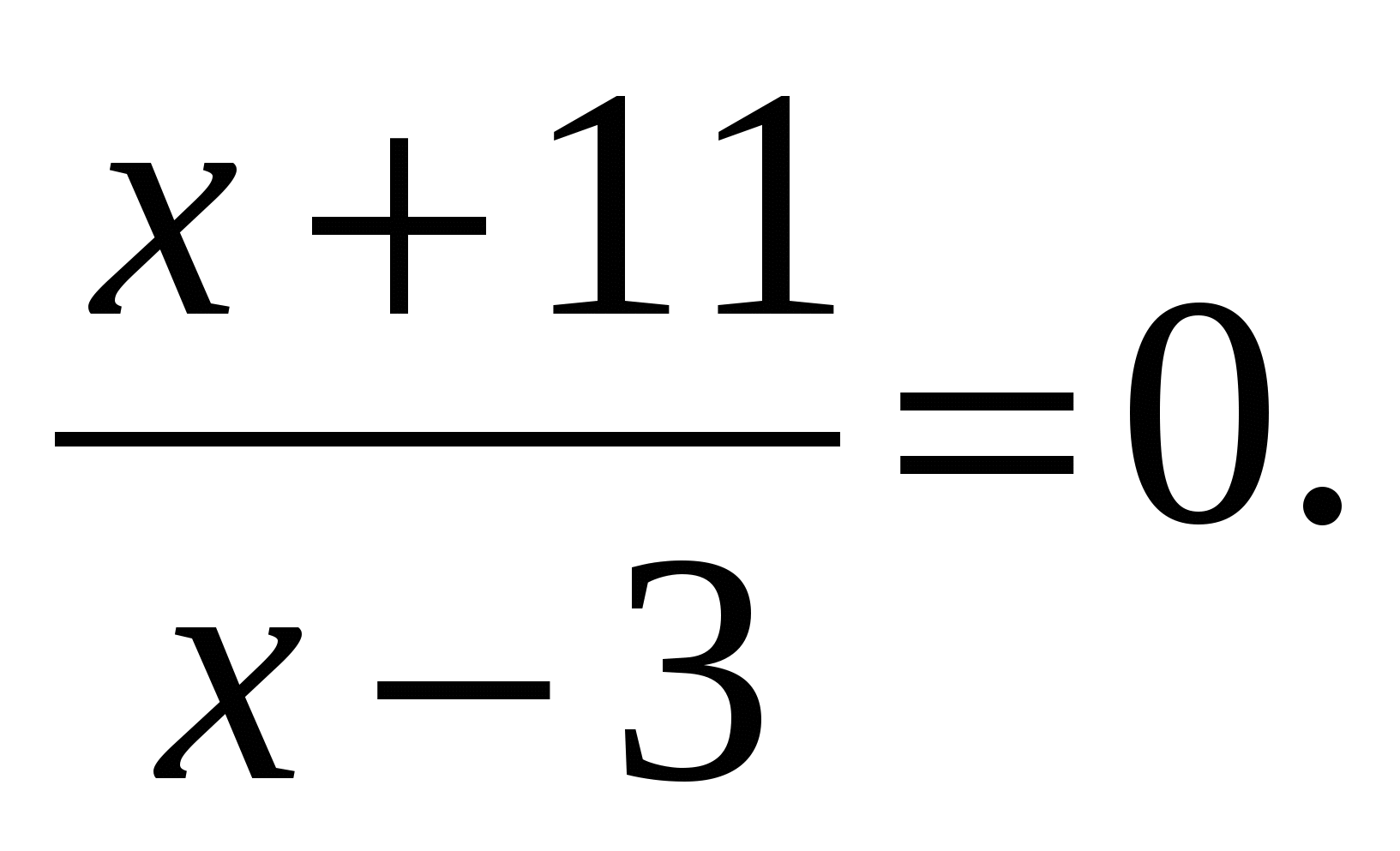
|
1) х=- 11
|
2) х1=11, х2= - 3
|
3) х = 3
|
4) нет корней
|
6
|
Решить неравенство 2х – 23 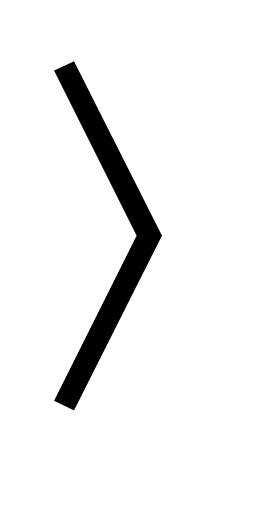 - 5 . - 5 .
|
1) х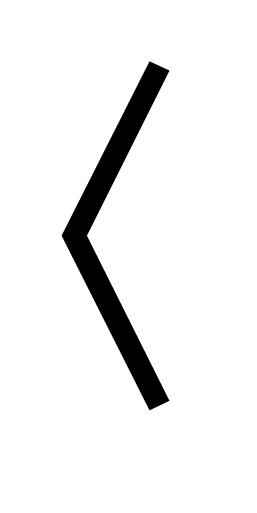 14 14
|
2) х 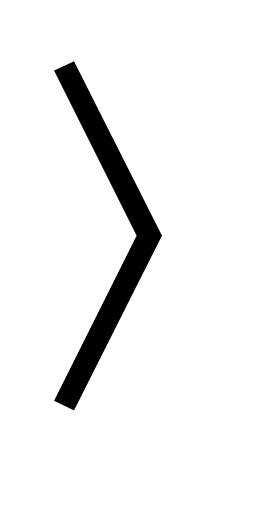 9 9
|
3) х 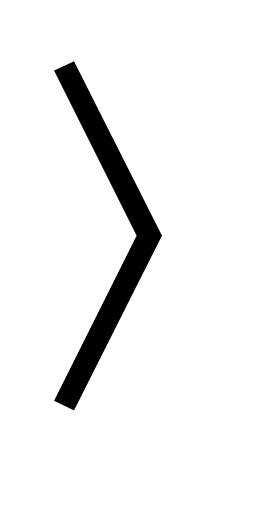 - 9 - 9
|
4) х 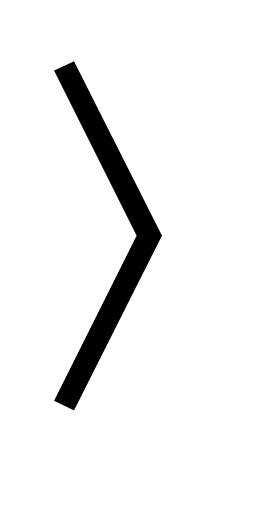 - 14 - 14
|
7
|
Решить неравенство 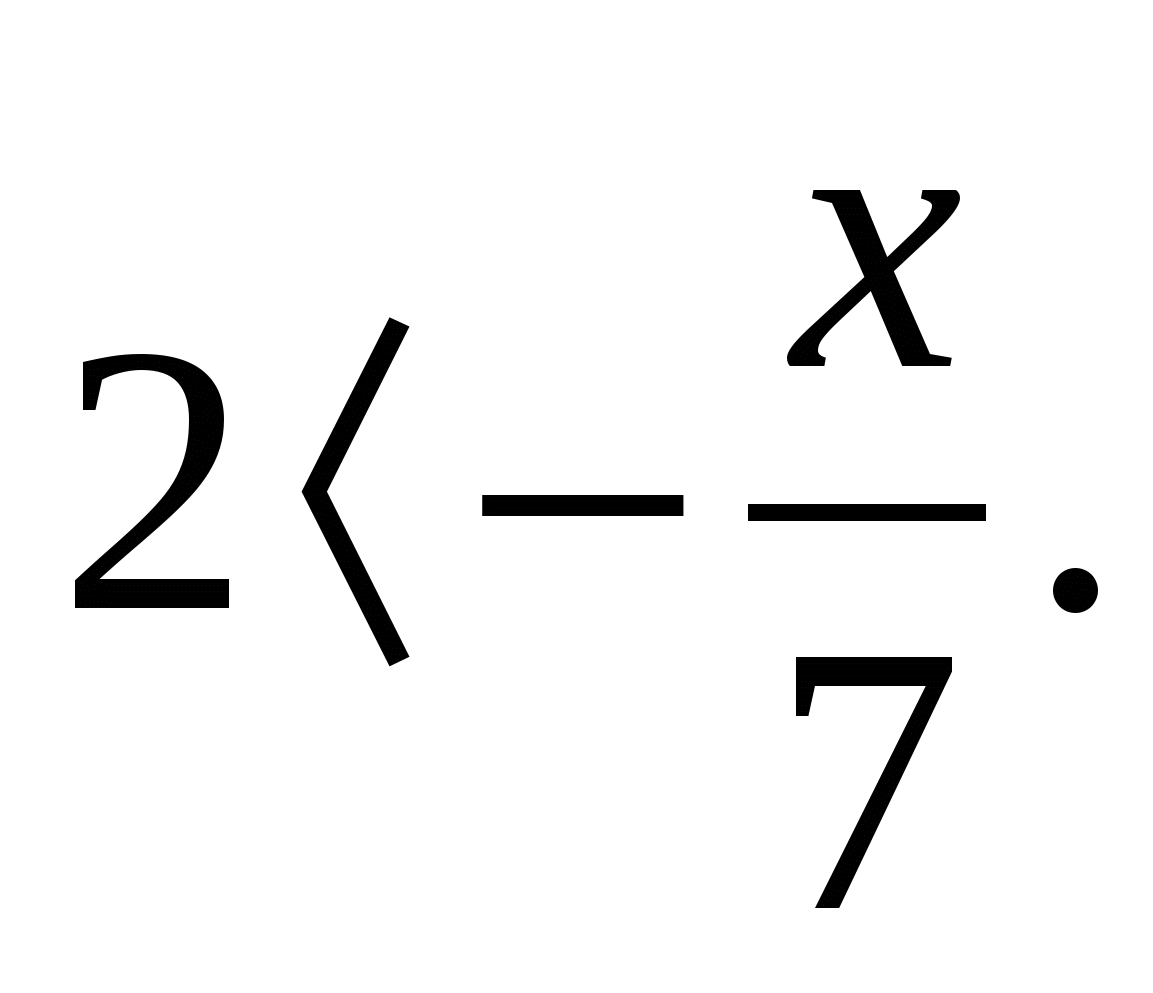
|
1) х 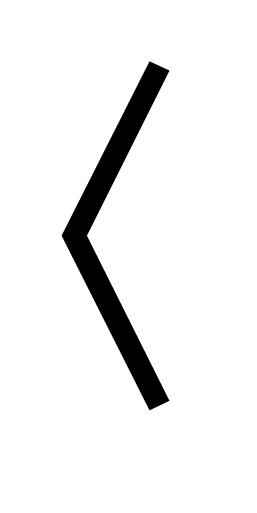 -2 -2
|
2) х 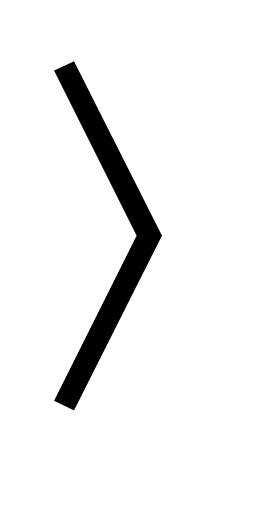 - 2 - 2
|
3) х 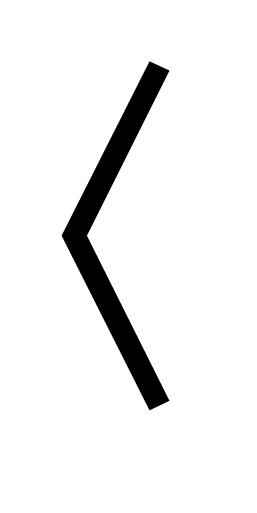 - 14 - 14
|
4) х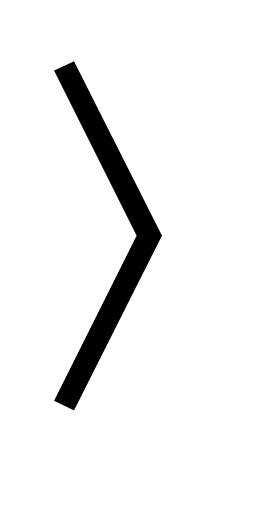 - 14 - 14
|
8
|
Указать наибольшее целое число, являющееся решением неравенства 2х - 7 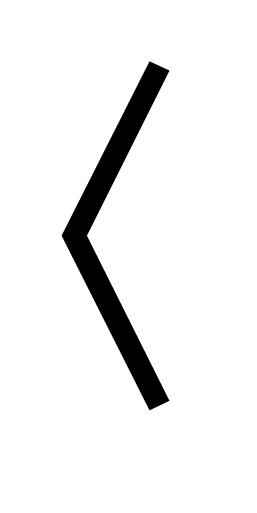 1. 1.
|
1) 3
|
2) 4
|
3) 2
|
4) 0
|
9
|
Решить систему неравенств 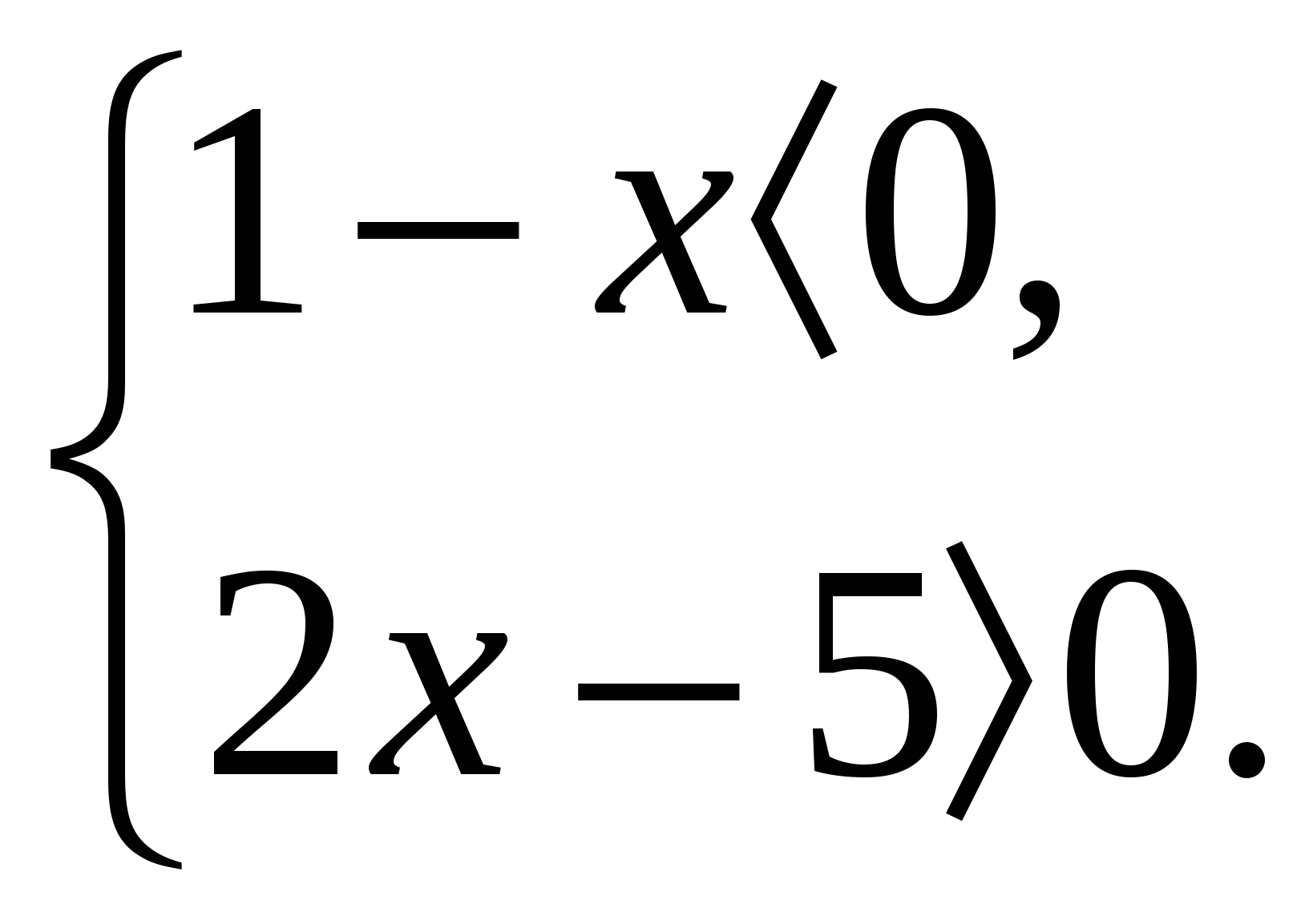
|
1) (2,5; 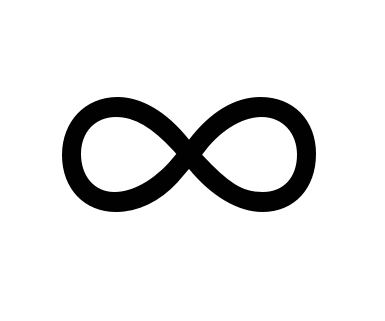 ) )
|
2) (1; 2,5)
|
3) (1;  ) )
|
4) решений нет
|
10
|
Сколько целых решений имеет неравенство - 1 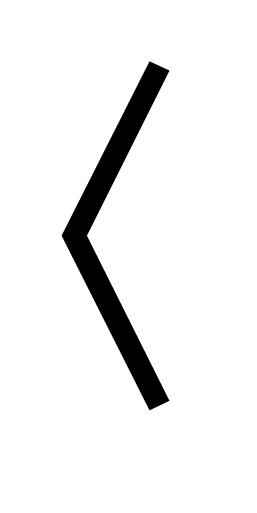 х х 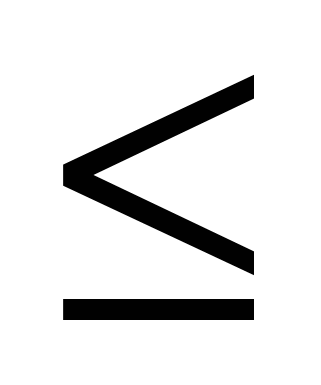 2 ? 2 ?
|
1) 1
|
2) 2
|
3) 3
|
4) 4
|
11
|
Решить уравнение ׀ х׀= 5
|
1) х ≥ 5; х 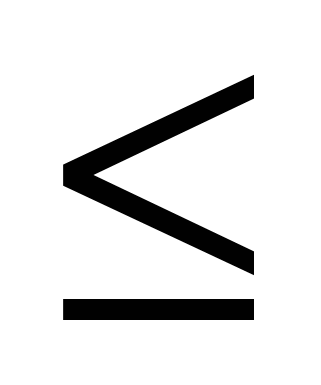 -5 -5
|
2) - 5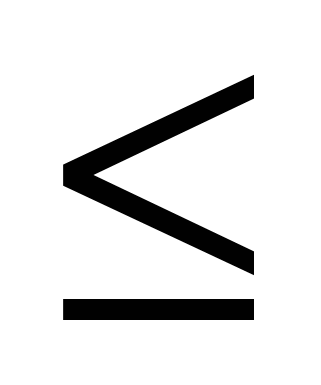 х х 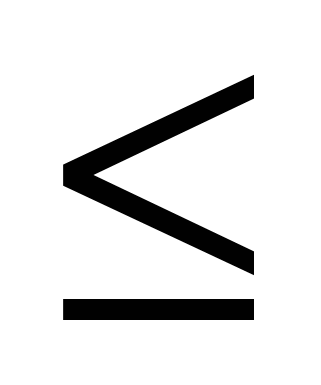 5 5
|
3) х = 5
|
4) х = ± 5
|
12
|
Решить уравнение 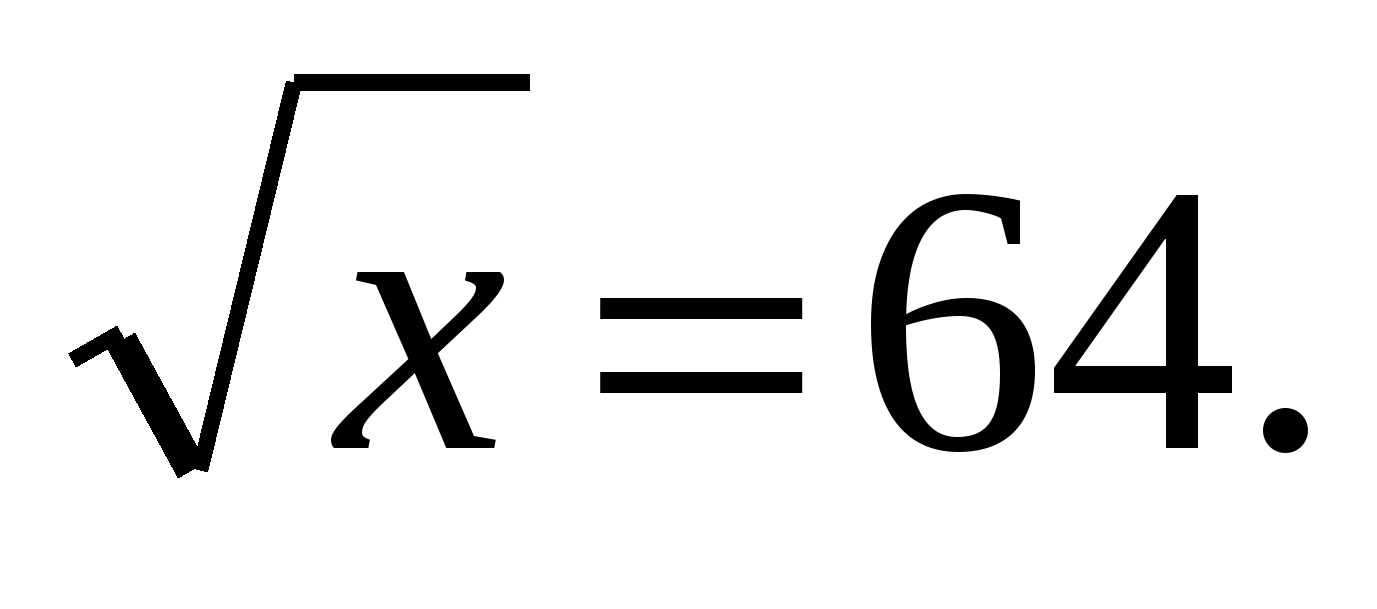
|
1) х = 32
|
2) х = 16
|
3) х = 8
|
4) х = 4096
|
13
|
Вычислить 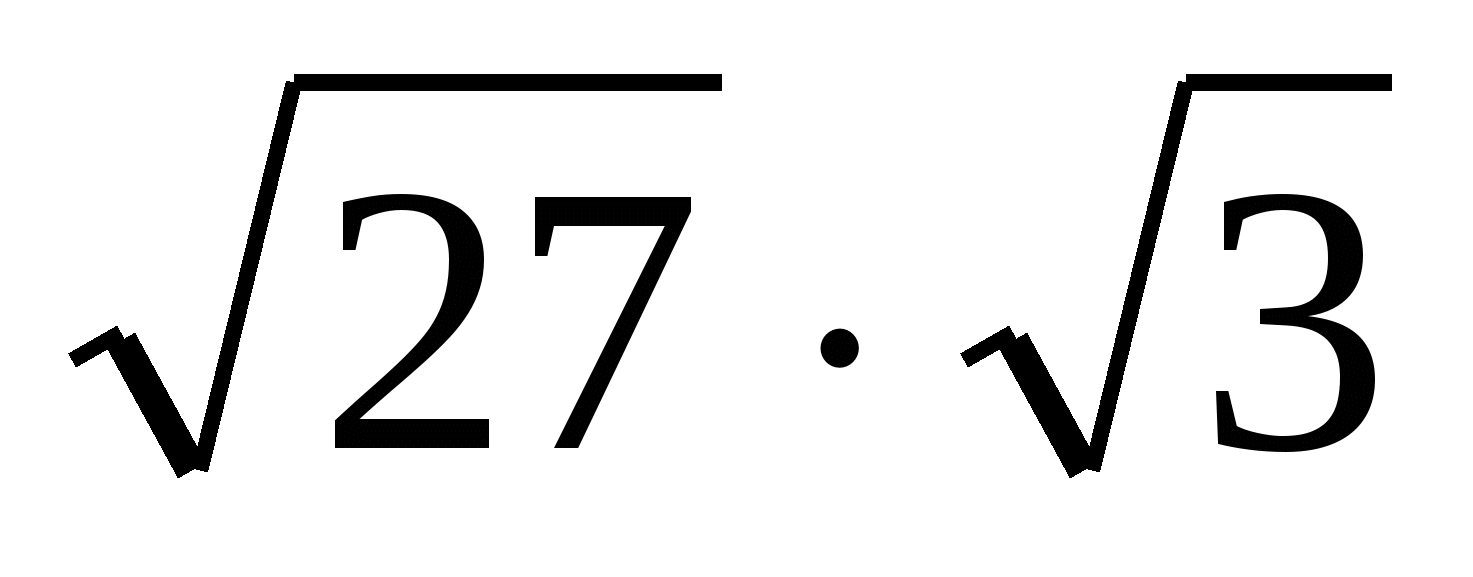
|
1) 4
|
2) 27
|
3) 9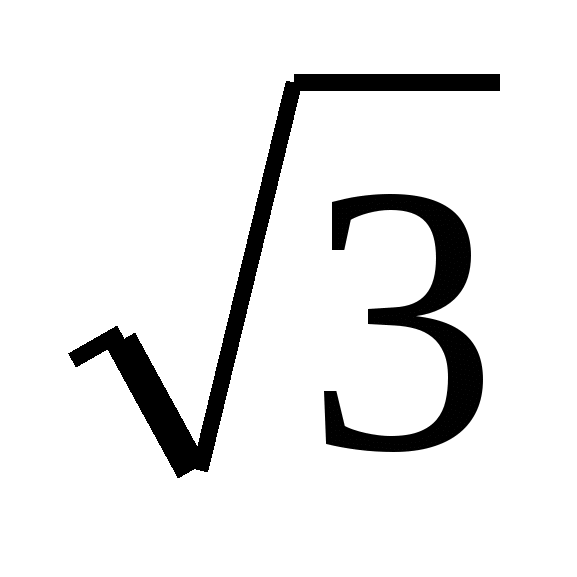
|
4) 9
|
14
|
Вычислить 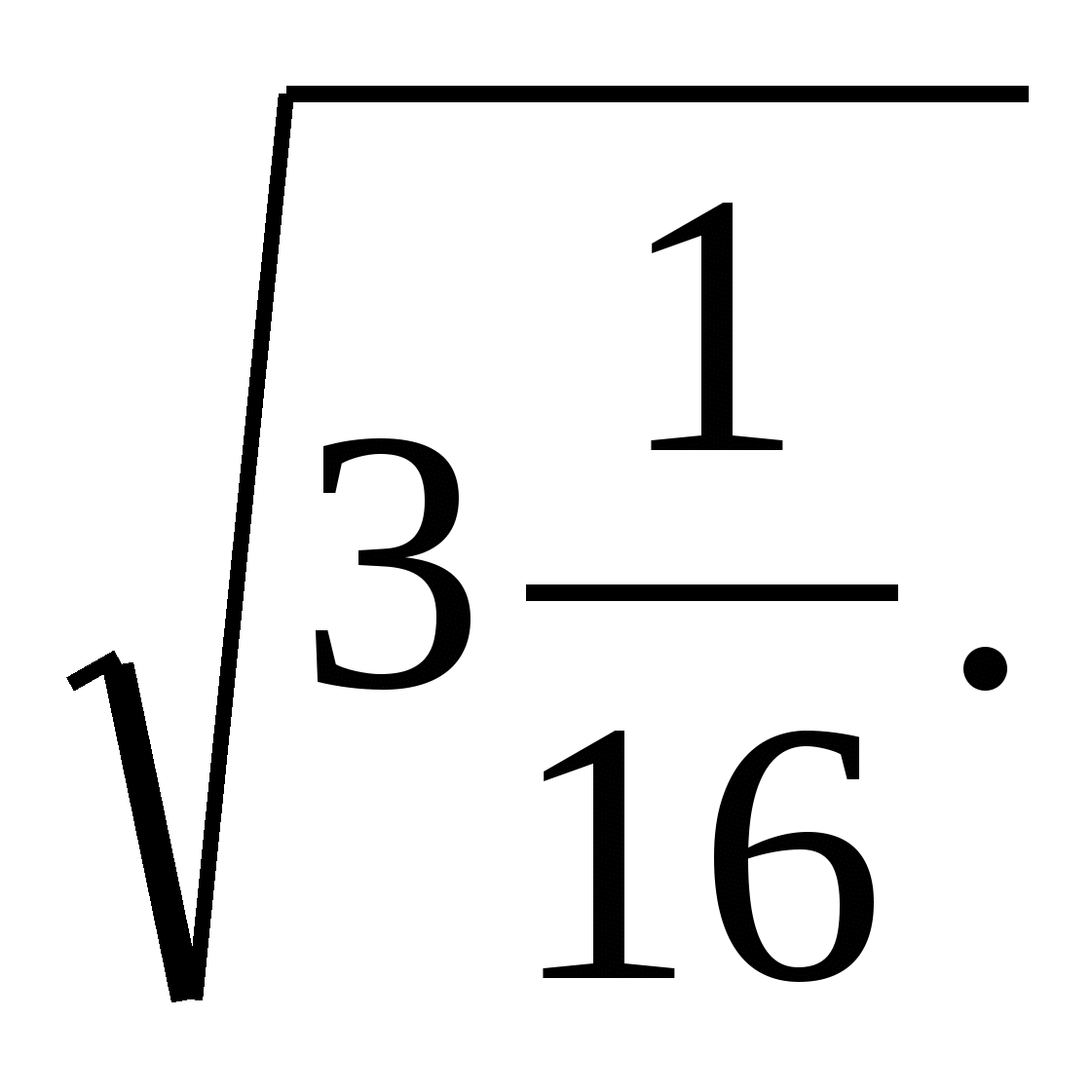
|
1) 1,75
|
2) 3,25
|
3)  
|
4) 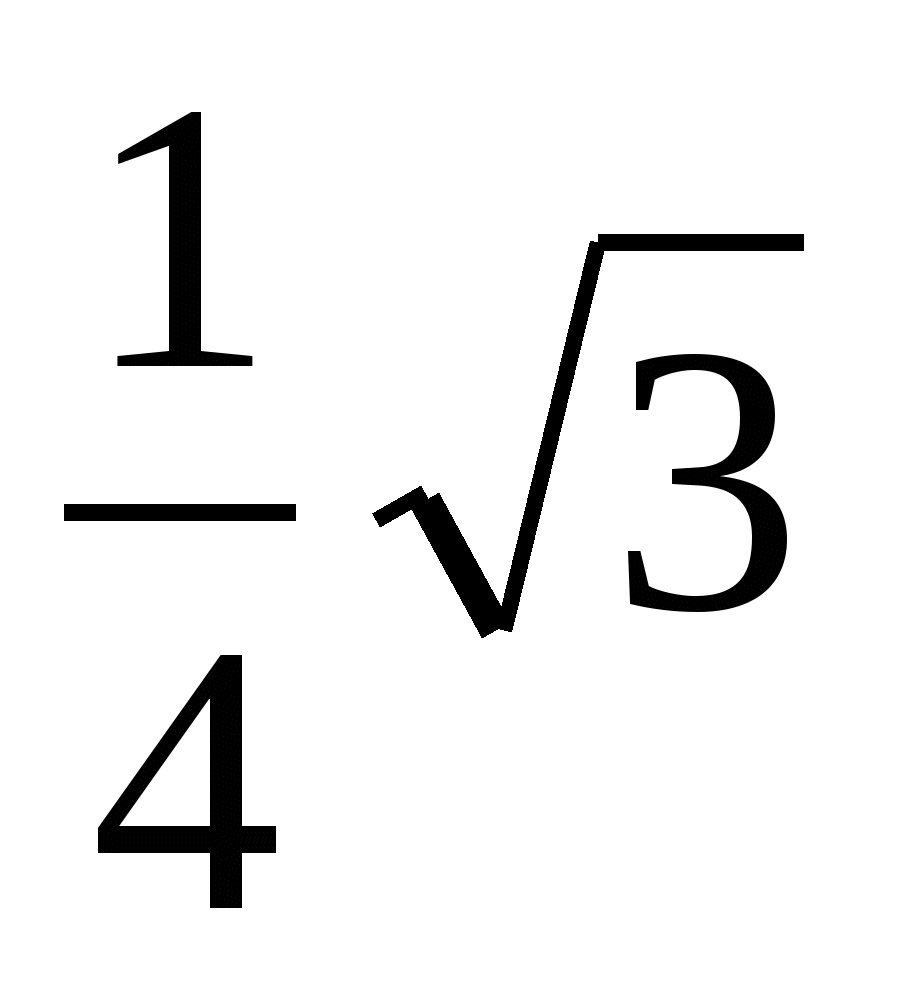
|
15
|
Вынести множитель за знак корня 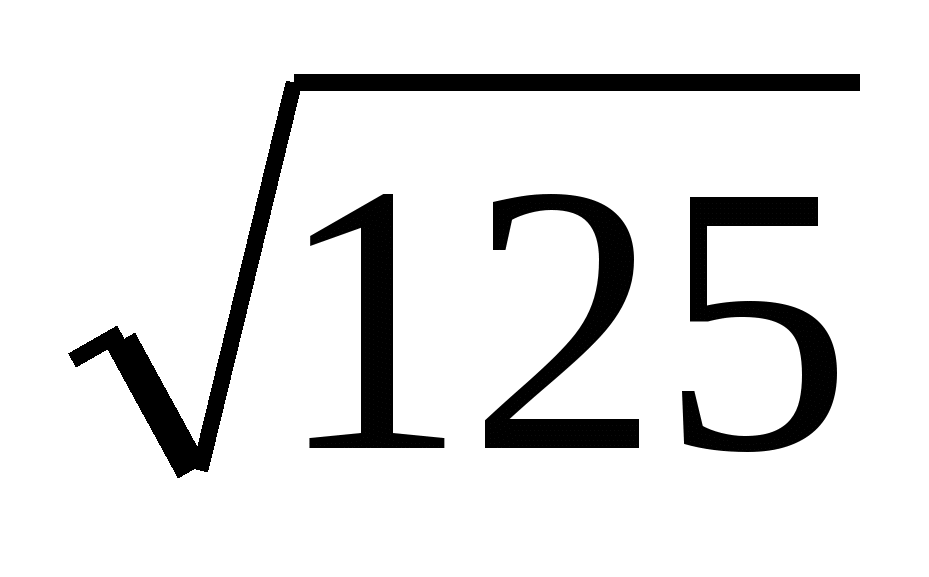 . .
|
1) 5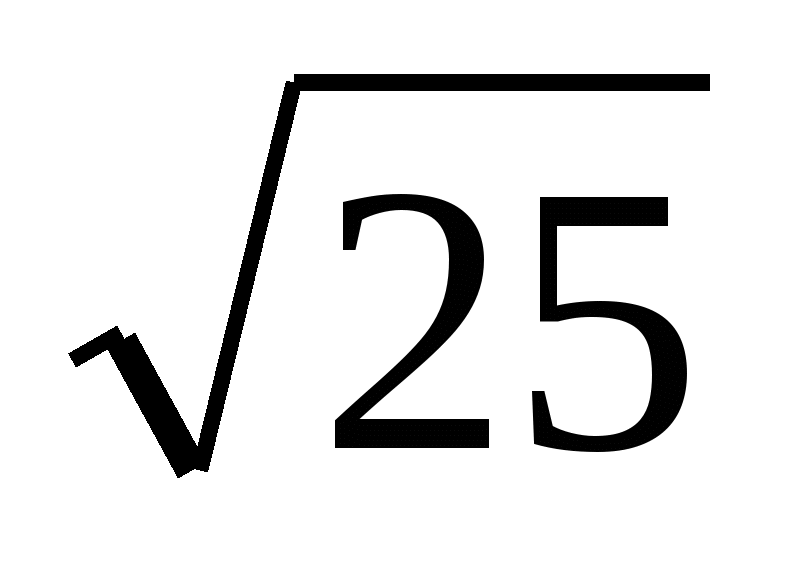
|
2) 25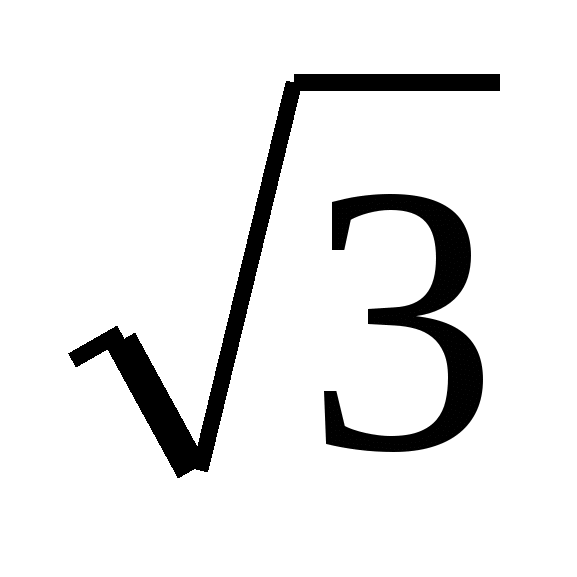
|
3) 5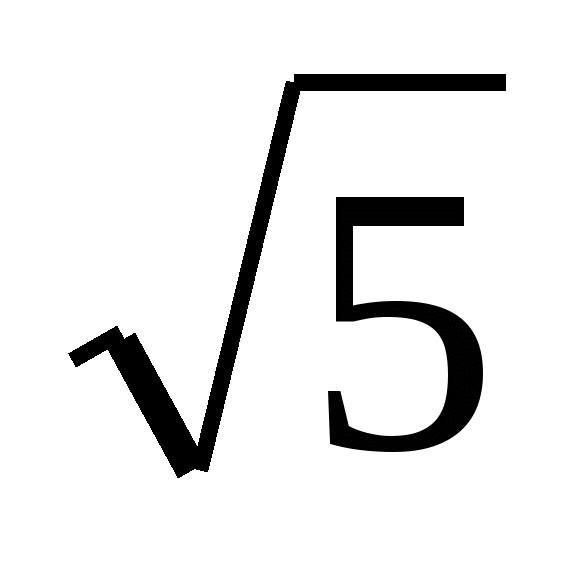
|
4) 5
|
16
|
Внести множитель под знак корня - 2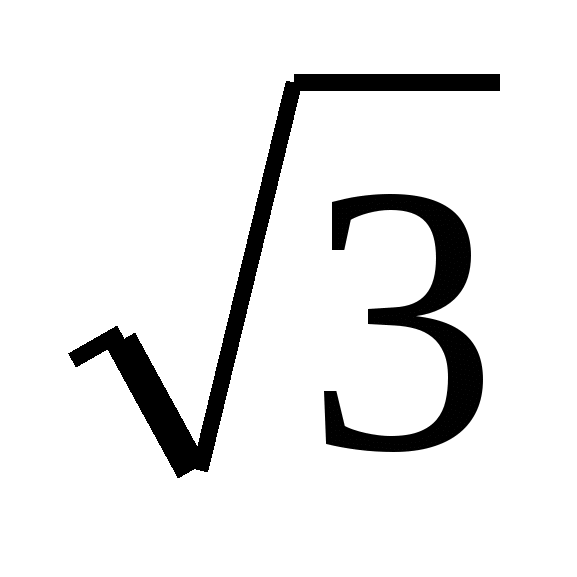
|
1) 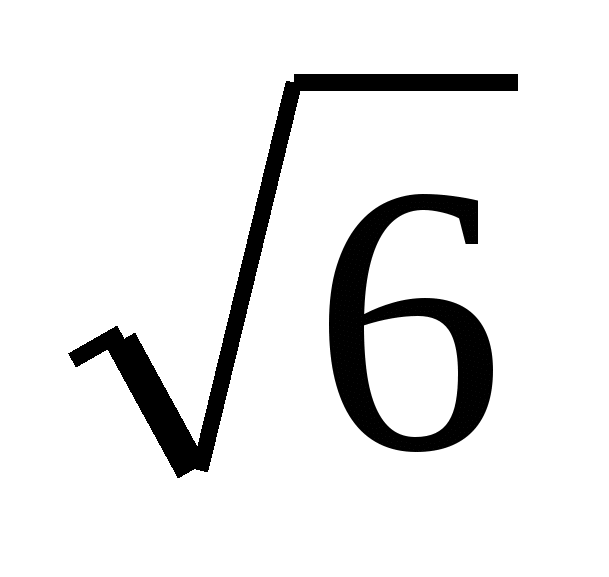
|
2) - 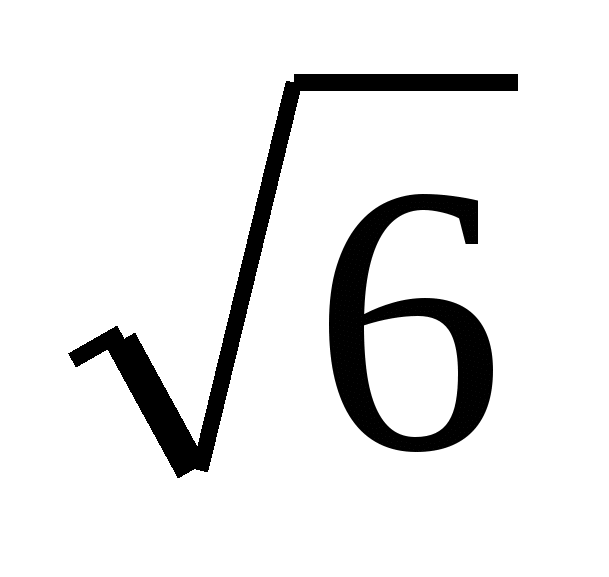
|
3) 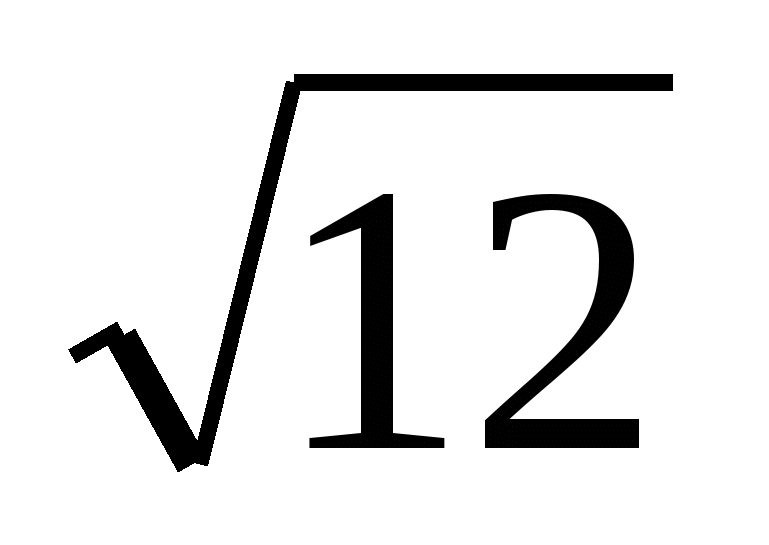
|
4) - 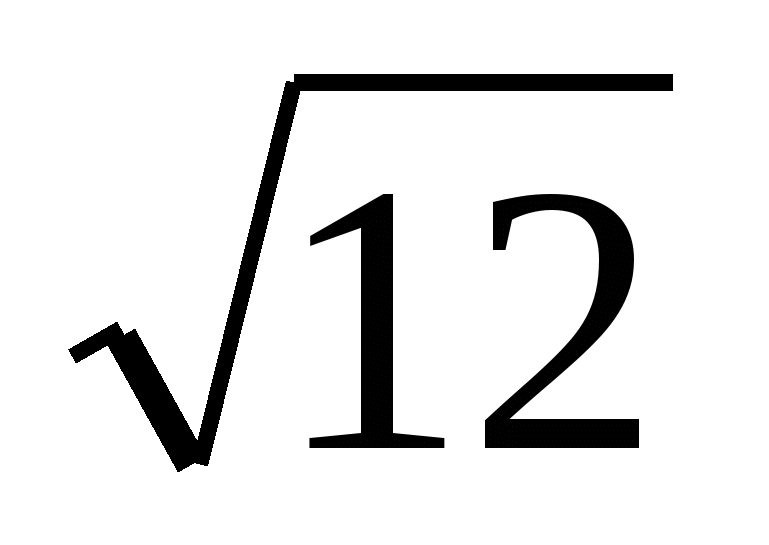
|
17
|
Решить уравнение х2 = 64
|
1) 8
|
2) ± 8
|
3) 32
|
4) ±32
|
18
|
Найти корни уравнения х2 + х = 0.
|
1) ±1; 0
|
2) 1; 0
|
3) – 1; 0
|
4) 0
|
19
|
Решить уравнение 3х2 + 8х – 3 = 0.
|
1) 3; 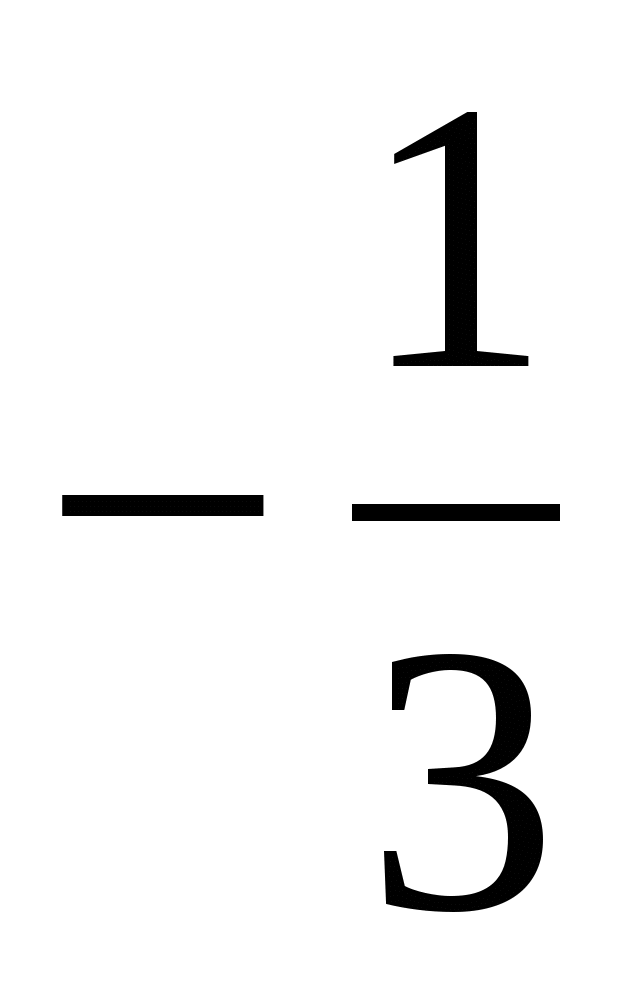
|
2) -3; 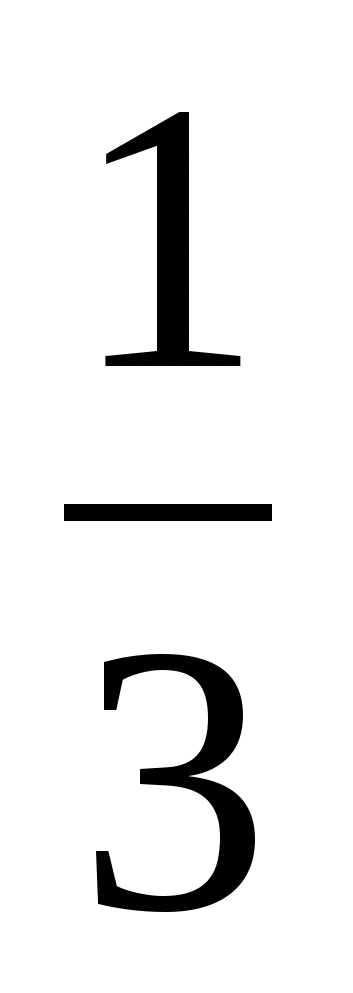
|
3) 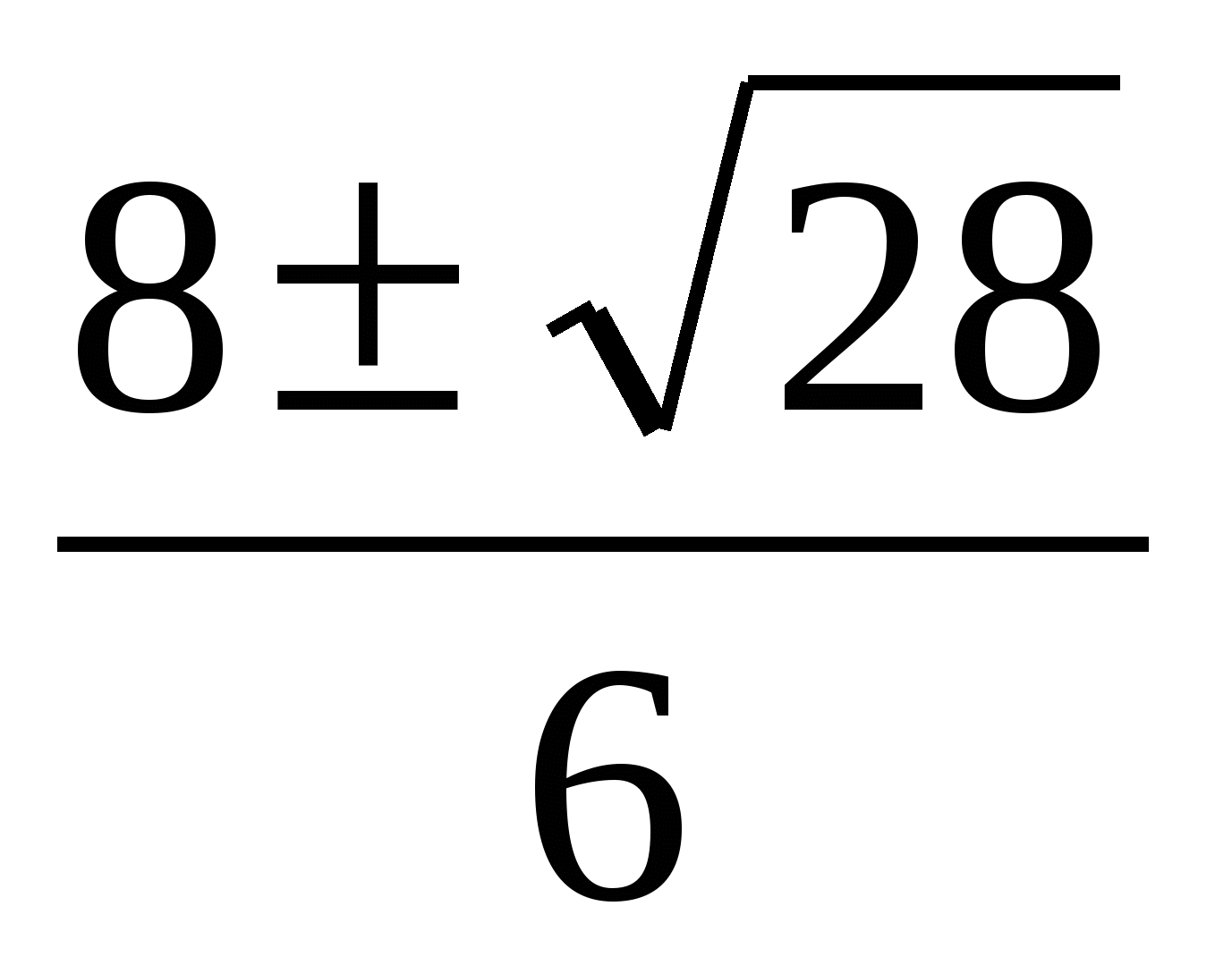
|
4) нет корней
|
20
|
По теореме Виета найти сумму корней уравнения х2 + 5х - 3 = 0
|
1) - 3
|
2) 5
|
3) - 5
|
4) 3
|
|
|
|
 Скачать 0.52 Mb.
Скачать 0.52 Mb.