Рабочая программа по геометрии 11 класс (по учебнику Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев, Л. С. Киселева, Э. Г. Позняк)
 Скачать 0.58 Mb. Скачать 0.58 Mb.
|
Контрольная работа №1 Г- 11 по теме «Метод координат в пространстве» I вариант. №1. Найдите координаты вектора  , если , если  , , 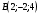 . .№2. Даны векторы  и и  . Найдите . Найдите 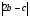 . .№3. Изобразите систему координат Oxyz и постройте точку 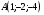 . Найдите расстояние от этой точки до координатных плоскостей. . Найдите расстояние от этой точки до координатных плоскостей.Контрольная работа №1 Г- 11 по теме «Метод координат в пространстве» II вариант. №1. Найдите координаты вектора 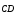 , если , если 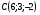 , , 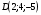 . .№2. Даны векторы 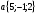 и и 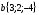 . Найдите . Найдите 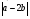 . .№3. Изобразите систему координат Oxyz и постройте точку  . Найдите расстояние от этой точки до координатных плоскостей. . Найдите расстояние от этой точки до координатных плоскостей.Контрольная работа №1 Г- 11 по теме «Метод координат в пространстве» III вариант. №1. Найдите координаты вектора  , если , если  , ,  . .№2. Даны векторы 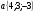 и и 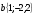 . Найдите . Найдите 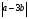 . .№3. Изобразите систему координат Oxyz и постройте точку  . Найдите расстояние от этой точки до координатных плоскостей. . Найдите расстояние от этой точки до координатных плоскостей.Контрольная работа №1 Г- 11 по теме «Метод координат в пространстве» IV вариант. №1. Найдите координаты вектора  , если , если 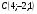 , ,  . .№2. Даны векторы 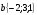 и и 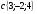 . Найдите . Найдите  . .№3. Изобразите систему координат Oxyz и постройте точку 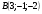 . Найдите расстояние от этой точки до координатных плоскостей. . Найдите расстояние от этой точки до координатных плоскостей.Контрольная работа №2 Г- 11 по теме «Скалярное произведение векторов» I вариант. №1. Вычислите скалярное произведение векторов 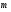 и и 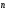 , если , если 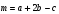 , , 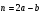 , , 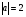 , , 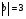 , ,  , , 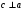 , ,  . .№2. Дан куб АВСDA1B1C1D1. Найдите угол между прямыми AC и DC1. №3. Даны точки А(0;1;2), В(  , С( , С(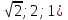 , D(0;2;1). Докажите, что АВСD – ромб. , D(0;2;1). Докажите, что АВСD – ромб.Контрольная работа №2 Г- 11 по теме «Скалярное произведение векторов» II вариант. №1. Вычислите скалярное произведение векторов 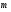 и и 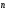 , если , если 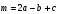 , , 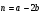 , ,  , ,  , ,  , , 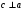 , ,  . .№2. Дан куб АВСDA1B1C1D1. Найдите угол между прямыми AD1 и BM, где M – середина ребра DD1. №3. Даны точки А(14;-8;-1), В( 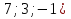 , С( , С( , D(1;-7;-1). Докажите, что АВСD – ромб. , D(1;-7;-1). Докажите, что АВСD – ромб.Контрольная работа №2 Г- 11 по теме «Скалярное произведение векторов» III вариант. №1. Вычислите скалярное произведение векторов 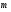 и и 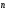 , если , если 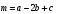 , ,  , ,  , ,  , , 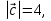 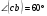 , , 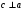 , ,  . .№2. Дан куб АВСDA1B1C1D1. Найдите угол между прямыми AB1 и D1C. №3. Даны точки А(1;1;5), В(  , С( , С(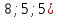 , D(5;-1;5). Докажите, что АВСD – прямоугольник. , D(5;-1;5). Докажите, что АВСD – прямоугольник.Контрольная работа №2 Г- 11 по теме «Скалярное произведение векторов» IV вариант. №1. Вычислите скалярное произведение векторов 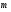 и и 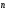 , если , если  , ,  , , 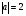 , ,  , , 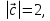  , ,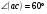 , ,  . .№2. Дан куб АВСDA1B1C1D1. Найдите угол между прямыми В1D и АР, где Р – середина ребра ВС. №3. Даны точки А(8;4;3), В( 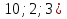 , С( , С(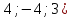 , D(2;-2;3). Докажите, что АВСD – прямоугольник. , D(2;-2;3). Докажите, что АВСD – прямоугольник.Контрольная работа №3 по теме «Цилиндр. Конус» Г- 11 I вариант. №1. Осевое сечение цилиндра – квадрат, площадь основания цилиндра равна 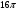 см2. Найдите площадь полной поверхности цилиндра. см2. Найдите площадь полной поверхности цилиндра.№2. Высота конуса 6 см, угол при вершине осевого сечения равен 120º. Найдите: а) площадь сечения конуса плоскостью, проходящей через две образующие, угол между которыми равен 30º; б) площадь боковой поверхности конус. №3. Радиусы оснований усечённого конуса 3 см и 7 см, образующая 5 см. Найти площадь осевого сечения. Контрольная работа №3 по теме «Цилиндр. Конус» Г- 11 II вариант. №1. Осевое сечение цилиндра – квадрат, диагональ которого равна 4 см. Найдите площадь полной поверхности цилиндра. №2. Радиус основания конуса равен 6 см, а образующая наклонена к плоскости основания под углом 30º. Найдите: а) площадь сечения конуса плоскостью, проходящей через две образующие, угол между которыми равен 60º; б) площадь боковой поверхности конуса. №3. Радиусы оснований усечённого конуса 11 см и 16 см, образующая 13 см. Найти расстояние от центра меньшего основания до окружности большего основания. Контрольная работа №3 по теме «Цилиндр. Конус» Г- 11 III вариант. №1. Осевое сечение цилиндра – квадрат, площадь основания цилиндра равна 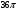 см2. Найдите площадь полной поверхности цилиндра. см2. Найдите площадь полной поверхности цилиндра.№2. Высота конуса 18 см, угол при вершине осевого сечения равен 90º. Найдите: а) площадь сечения конуса плоскостью, проходящей через две образующие, угол между которыми равен 60º; б) площадь боковой поверхности конуса. №3. Радиусы оснований усечённого конуса 4 см и 10 см, образующая 8 см. Найти площадь осевого сечения. Контрольная работа №3 по теме «Цилиндр. Конус» Г- 11 IV вариант. №1. Осевое сечение цилиндра – квадрат, диагональ которого равна 10  см. Найдите площадь полной поверхности цилиндра. см. Найдите площадь полной поверхности цилиндра.№2. Радиус основания конуса равен 6 см, а образующая наклонена к плоскости основания под углом 60º. Найдите: а) площадь сечения конуса плоскостью, проходящей через две образующие, угол между которыми равен 45º; б) площадь боковой поверхности конуса. №3. Радиусы оснований усечённого конуса 2 см и 10 см, образующая 6 см. Найти расстояние от центра меньшего основания до окружности большего основания. Контрольная работа №3 по теме «Цилиндр. Конус» Г- 11 V вариант. №1. Осевое сечение цилиндра – квадрат, площадь основания цилиндра равна  см2. Найдите площадь полной поверхности цилиндра. см2. Найдите площадь полной поверхности цилиндра.№2. Высота конуса 24 см, угол при вершине осевого сечения равен 60º. Найдите: а) площадь сечения конуса плоскостью, проходящей через две образующие, угол между которыми равен 60º; б) площадь боковой поверхности конус. №3. Радиусы оснований усечённого конуса 4 см и 8 см, образующая 5 см. Найти площадь осевого сечения. Контрольная работа №4 по теме «Сфера и шар» Г- 11 I вариант. №1. Диаметр шара равен 2m. Через конец диаметра проведена плоскость под углом 45º к нему. Найдите длину линии пересечения сферы этой плоскостью. №2. Точка А(0;  ; ;  ) лежит на сфере с центром О (3; 0; 0). Запишите уравнение сферы. ) лежит на сфере с центром О (3; 0; 0). Запишите уравнение сферы.№3. Сечение шара плоскостью, удаленной от его центра на 8 см, имеет площадь 36 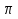 см2. Определите площадь поверхности шара. см2. Определите площадь поверхности шара.№4. Докажите, что уравнение х2 + у2 + z2 – 6x – 4y – 8z = 4 является уравнением сферы. Найдите центр и радиус сферы. Контрольная работа №4 по теме «Сфера и шар» Г- 11 II вариант. №1. Диаметр шара равен 4a. Через конец диаметра проведена плоскость под углом 30º к нему. Найдите площадь сечения шара этой плоскостью. №2. Центр сферы имеет координаты С(1; 2; 0). Сфера проходит через точку А(  ; 0; 5). Запишите уравнение сферы. ; 0; 5). Запишите уравнение сферы.№3. Линия пересечения сферы и плоскости, удаленной от его центра на 8 см, имеет длину 12 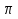 см. Найдите площадь поверхности шара. см. Найдите площадь поверхности шара.№4. Докажите, что уравнение х2 + у2 + z2 – 8x – 6y = 6 является уравнением сферы. Найдите центр и радиус сферы. Контрольная работа №4 по теме «Сфера и шар» Г- 11 III вариант. №1. Диаметр шара равен 6c. Через конец диаметра проведена плоскость под углом 60º к нему. Найдите длину линии пересечения сферы этой плоскостью. №2. Напишите уравнение сферы с центром в точке А(2;-1;6), проходящей через точку О (4; 2; 5). №3. Сечение шара плоскостью, удаленной от его центра на 4 см, имеет площадь 9 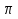 см2. Определите площадь поверхности шара. см2. Определите площадь поверхности шара.№4. Докажите, что уравнение х2 + у2 + z2 + 8y – 4z = 8 является уравнением сферы. Найдите центр и радиус сферы. Контрольная работа №4 по теме «Сфера и шар» Г- 11 IV вариант. №1. Диаметр шара равен 8a. Через конец диаметра проведена плоскость под углом 45º к нему. Найдите площадь сечения шара этой плоскостью. №2. Центр сферы имеет координаты А(-2; 1; -4). Сфера проходит через точку В(6; -7; 10). Запишите уравнение сферы. №3. Линия пересечения сферы и плоскости, удаленной от его центра на 3 см, имеет длину 8 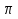 см. Найдите площадь поверхности шара. см. Найдите площадь поверхности шара.№4. Докажите, что уравнение х2 + у2 + z2 – 8x + 4y = 10 является уравнением сферы. Найдите центр и радиус сферы. Контрольная работа №4 по теме «Сфера и шар» Г- 11 V вариант. №1. Диаметр шара равен 10c. Через конец диаметра проведена плоскость под углом 30º к нему. Найдите длину линии пересечения сферы этой плоскостью. №2. Напишите уравнение сферы с центром в точке А(-6;2;4), проходящей через точку О (2; 4; -8). №3. Сечение шара плоскостью, удаленной от его центра на 3 см, имеет площадь 16 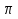 см2. Определите площадь поверхности шара. см2. Определите площадь поверхности шара.№4. Докажите, что уравнение х2 + у2 + z2 + 4х – 4z = 12 является уравнением сферы. Найдите центр и радиус сферы. Контрольная работа №5 по теме «Объёмы тел» Г- 11 I вариант. №1. Апофема правильной треугольной пирамиды равна 4 см, а двугранный угол при основании равен 60º. Найдите объем пирамиды. №2. В цилиндр вписана призма. Основанием призмы служит прямоугольный треугольник, катет которого равен 2a, а прилежащий угол равен 60º. Диагональ большой боковой грани призмы составляет с плоскостью ее основания угол 45º. Найдите объем цилиндра. Контрольная работа №5 по теме «Объёмы тел» Г- 11 II вариант. №1. В правильной четырёхугольной пирамиде плоский угол при вершине равен 60º, длина бокового ребра равна 8 см. Найдите объем пирамиды. №2. В конус вписана пирамида. Основанием пирамиды служит прямоугольный треугольник, катет которого равен 2a, а прилежащий угол равен 30º. Боковая грань пирамиды, проходящая через данный катет, составляет с плоскостью основания угол 45º. Найдите объем конуса. Контрольная работа №5 по теме «Объёмы тел» Г- 11 III вариант. №1. Боковое ребро правильной треугольной пирамиды равно 4 см. Плоский угол при вершине равен 60º. Найдите объем пирамиды. №2. Боковые рёбра четырёхугольной пирамиды составляют с основанием угол 45º. Найдите объём описанного около неё конуса, если сторона пирамиды равна а см. Контрольная работа №5 по теме «Объёмы тел» Г- 11 IV вариант. №1. Апофема правильной четырёхугольной пирамиды равна 6 см, а двугранный угол при основании равен 30º. Найдите объем пирамиды. №2. В цилиндр вписана призма. Основанием призмы служит квадрат, сторона которого равна a. Диагональ боковой грани призмы составляет с плоскостью ее основания угол 45º. Найдите объем цилиндра. Контрольная работа №5 по теме «Объёмы тел» Г- 11 V вариант. №1. Боковое ребро правильной треугольной пирамиды равно 10 см и составляет с плоскостью основания угол 60º. Найдите объем пирамиды. №2. Цилиндр и конус имеют равные радиусы оснований и равные высоты. Объём цилиндра равен 60 см3. Найдите объём конуса. Контрольная работа №5 по теме «Объёмы тел» Г- 11 VI вариант. №1. Боковое ребро правильной треугольной пирамиды равно 6 см и составляет с плоскостью основания угол 60º. Найдите объем пирамиды. №2. Цилиндр и конус имеют равные радиусы оснований и равные высоты. Объём конуса равен 40 см3. Найдите объём цилиндра. Контрольная работа №6 по теме «Объём шара и площадь сферы» Г- 11 I вариант. №1. Диаметр шара равен высоте конуса, образующая которого составляет с плоскостью основания угол 60º. Найдите отношение объемов конуса и шара. №2. Объем цилиндр равен 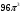 см3, площадь его осевого сечения – 48 см2. Найдите площадь сферы, описанного около цилиндра. см3, площадь его осевого сечения – 48 см2. Найдите площадь сферы, описанного около цилиндра.Контрольная работа №6 по теме «Объём шара и площадь сферы» Г- 11 II вариант. №1. В конус, осевое сечение которого есть правильный треугольник, вписан шар. Найдите площадь сферы, если образующая конуса равна 6 см. №2. Диаметр шара равен диагонали куба. Найдите отношение объемов шара и куба. Контрольная работа №6 по теме «Объём шара и площадь сферы» Г- 11 III вариант. №1. Диаметр шара равен образующей конуса. Образующая конуса составляет с плоскостью основания угол 30º. Найдите отношение объемов конуса и шара. №2. Прямоугольный параллелепипед описан около сферы. Найдите объём параллелепипеда, если площадь сферы равна 16 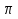 см2. см2.Контрольная работа №6 по теме «Объём шара и площадь сферы» Г- 11 IV вариант. №1. Около конуса, осевое сечение которого есть правильный треугольник, описан шар. Найдите площадь сферы, если образующая конуса равна 6 см. №2. Диаметр шара равен боковому ребру правильной четырёхугольной пирамиды. Сечение пирамиды, проходящее через её высоту и боковое ребро, является равносторонним треугольником. Найдите отношение объемов шара и пирамиды. Контрольная работа №6 по теме «Объём шара и площадь сферы» Г- 11 V вариант. №1. Прямоугольный параллелепипед вписан в сферу. Найдите объём параллелепипеда, если площадь сферы равна 36 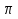 см2. см2.№2. Диаметр шара равен высоте цилиндра, осевое сечение которого есть квадрат. Найдите отношение объемов шара и цилиндра. Контрольная работа №6 по теме «Объём шара и площадь сферы» Г- 11 VI вариант. №1. Найдите объём шара, если площадь сферы равна 81 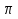 см2. см2.№2. В правильной четырёхугольной призме сторона основания равна 6 см, боковое ребро равно 2  см. Найдите объём описанного около призмы шара. см. Найдите объём описанного около призмы шара.Контрольная работа №7 (итоговая) Г- 11 I вариант. В правильной четырёхугольной пирамиде МАВСD сторона основания равна 6 см, а боковое ребро 5см. Найдите:
Контрольная работа №7 (итоговая) Г- 11 II вариант. В правильной треугольной пирамиде МАВС сторона основания равна 4  см, а боковое ребро 5 см. Найдите: см, а боковое ребро 5 см. Найдите:
Контрольная работа №7 (итоговая) Г- 11 III вариант. В правильной четырёхугольной пирамиде МАВСD сторона основания равна 8 см наклонено к плоскости основания под углом 60º. Найдите:
Контрольная работа №7 (итоговая) Г- 11 IV вариант. В правильной треугольной пирамиде МАВС сторона основания равна 2 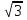 см, а боковые грани наклонены к основанию под углом 60º. Найдите: см, а боковые грани наклонены к основанию под углом 60º. Найдите:
|
 +
+ 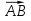 )
) 
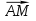 ;
;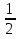 (
(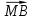 +
+ 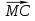 )
)  , где Е – середина ВС;
, где Е – середина ВС; +
+  , где Е – середина DС;
, где Е – середина DС;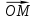 , где О – основание высоты пирамиды;
, где О – основание высоты пирамиды;