Тела вращения. Шар и сфера Шар
 Скачать 41.61 Kb. Скачать 41.61 Kb.
|
| Тела вращения. Шар и сфера Шар — геометрическое тело, ограниченное поверхностью, все точки которой отстоят на равном расстоянии от центра. Это расстояние называется радиусом шара. Шар образуется вращением полукруга около его неподвижного диаметра. Этот диаметр называется осью шара, а его оба конца — полюсами шара. Поверхность шара называется сферой. Примеры тел, имеющих форму шара или сферы:
Связанные определения
Свойства
Основные формулы
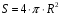 Примеры: Задача1.Радиус сферы увеличили в 3 раза. Во сколько раз увеличится площадь сферы? Дано: r – радиус исходной сферы, R – радиус новой сферы, R = 3r Найти: 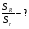 Решение. 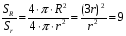 Ответ: в 9 раз. Задача 2. Шар радиуса 41 дм пересечен плоскостью, находящейся на расстоянии 9 дм от центра. Найдите площадь сечения (см. рис. 1). 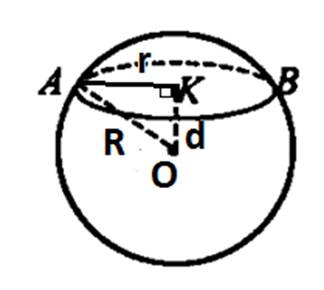 Рис. 1. Решение: 1. Так как, d 2. Рассмотрим треугольник AOK – прямоугольный. 3. Подставим значение радиуса в формулу площади круга: Ответ: 1600π дм2. Задача 3. Стороны треугольника касаются сферы радиуса 5 см. Найдите расстояние от центра сферы до плоскости треугольника, если его стороны равны 14 см, 14 см и 15 см (см. рис. 2). 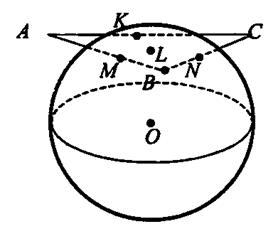 Рис. 2. Решение: 1. Проведем перпендикуляр OL к плоскости треугольника. Обозначим точки M, N, K – точки касания сторон треугольника и сферы. Так как, 2. Из равенства треугольников, 3. Найдем ML. 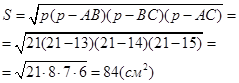 Отсюда, Чтобы найти OL, рассмотрим Ответ: 3 см. Задача 4. Радиус сферы равен 112 см. Точка, лежащая на плоскости, касательной к сфере, удалена от точки касания на 15 см. Найдите расстояние от этой точки до ближайшей к ней точки сферы. Решение: Нарисуем рисунок, и обозначим все данные (см. рис. 3). 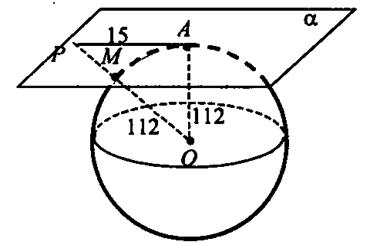 Рис. 3. 1) Треугольник OAP – прямоугольный. По теореме Пифагора, 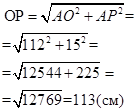 2) Ответ: 1 см. Задания 1. Шар, радиуса 41 дм, пересечен плоскостью на расстоянии 9 дм от центра Найдите площадь сечения. 2.Через середину радиуса шара проведена перпендикулярная ему плоскость. Как относится площадь полученного сечения к площади большого круга? 3. Радиус шара R. Через конец радиуса проведена плоскость под углом 600 к нему. Найти площадь сечения. 4. Город N находится на 600 северной широты. Какой путь совершает этот пункт в течение 1 ч. Вследствие вращения Земли вокруг своей оси? Радиус Земли принять равным 6000 км. 5. Найдите координаты центра и радиус сферы, заданной уравнением: а) x2+y2+z2=49; b) (x-3)2+(y+2)2+z2=2. |