Прямая пропорциональность в математике, физике и жизни
 Скачать 62.82 Kb. Скачать 62.82 Kb.
|
| Муниципальное общеобразовательное учреждение «Началовская средняя общеобразовательная школа» Приволжского района Астраханской области Конспект интегрированного урока математика+физика на тему: «Прямая пропорциональность в математике, физике и жизни.» в 7 классе подготовили учитель физики Ситникова Инесса Анатольевна, учитель математики Вакуленко Вера Сергеевна Астрахань 2010 «Прямая пропорциональность в математике, физике и жизни» Ситникова Инесса Анатольевна, учитель физики 1 категории МОУ «Началовская средняя общеобразовательная школа» Приволжского района Астраханской области Вакуленко Вера Сергеевна , учитель математики высшей категории МОУ «Началовская средняя общеобразовательная школа» Приволжского района Астраханской области Интегрированный урок математика+физика для 7 класса. Цели: Образовательные: 1.Систематизировать знания по теме «Линейная функция», привлечь внимание к понятию функции, используя исторические сведения. 2.Ввести новое понятие «Прямая пропорциональность». 3.Формирование знаний и умений по расчёту пути и времени движения. 4.Формирование навыков самоконтроля, умения применять правила в практической работе. 5.Закрепить основные методы и навыки техники построения и чтения графиков линейных функций. 6.Показать единство математики и физики через межпредметные связи. Развивающие: 1.Развитие исследовательских навыков. 2.Развитие внимания. 3.Развитие логического и творческого мышления. 4.Развитие самостоятельности, умения преодолевать трудности. Воспитательные: Воспитывать взаимное доверие и уважение учащихся во время урока. Оборудование: Компьютер, проектор. Ход урока. 1.Оргмомент. В окружающем нас мире происходят различные явления и процессы: физические, химические, экономические. Мы являемся свидетелями того, как одни переменные величины определяют значение других. Мы говорим в этом случае о функциональной зависимости этих переменных. Так вот понятие функции имеет большое значение и в курсе алгебры и в курсе физики. 2. Историческая справка. Ещё Вавилонские учёные в 4 веке до н.э. установили зависимость между площадью круга его радиусом: S=3r². Рене Декарт в 1637 году рассматривал функцию как изменение ординаты точки в зависимости от изменения её абсциссы, которая принимала только положительные значения. Впервые употребил название «функция» ( от латинского functio- совершение, выполнение) Г.Лейбниц в 1673 году. Под функцией он понимал отрезок, длина которого меняется по определённому закону. И.Ньютон называл переменную величину, которая меняется с течением времени, флюэнтой ( от fluere-текущая). Л.Эйлер в 1748 году вводит обозначение функции f:x и даёт ей такое определение: «Функция переменного количества есть аналитическое выражение, составленное каким-либо образом из этого количества и чисел или постоянных количеств.» 3.Актуализация опорных знаний. Вспомним функции, уже известные нам, одновременно повторим их важнейшие свойства, а также повторим понятия равномерного и неравномерного движения. Проведём блиц-опрос (раздаются листы самоконтроля, каждый ученик получит оценку) 1.Линейная функция задаётся формулой…(y=ax+b). 2.Областью определения её является…(множество действительных чисел). 3.Графиком линейной функции является…(прямая). 4.Изменение положения тела относительно другого тела с течением времени называют …(механическим движением) 5.У функции y=ax+b число a называется…(угловым коэффициентом прямой). 6.В случае а<0 график расположен …(во 2 и 4 четверти) 7.В случае а>0 график расположен …(в 1 и 3 четверти) 8.Движение, при котором тело в любые равные промежутки времени проходит равные пути, называется…(равномерным) 9.Пассажирский поезд за каждые 0,5 ч проходит расстояние 60 км, за 15 мин.-30 км, за 1мин.-2км. Какое это движение? (равномерное) 10.Автомобиль за 0,5 ч проходит расстояние 30 км, причём за первые 15 мин.-20 км, а за последующие -10 км. Какое это движение? (неравномерное) Заполняются листы самоконтроля и выставляются оценки. Норма оценок: 10 – «5», 8-9 – «4», 6-7 – «3». 4. Изучение нового понятия. Рассмотрим некоторые функции:
Как вы думаете, какая функция выделяется среди данных функций , чем? (Ответ: 3) у=7х, b=0) Таким образом, мы с вами подошли к новому понятию. Среди линейных функций особо выделяют случай, когда b=0. В этом случае функция принимает вид у=кх и называют её прямой пропорциональностью. Это название объясняется тем, что две величины у и х называют прямо пропорциональными, если их отношение равно конкретному числу, отличному от нуля. Здесь у/х=к, это число к называют коэффициентом пропорциональности. Многие реальные ситуации моделируются с помощью прямой пропорциональности. Например: 1.Стоимость у и число х батонов хлеба по цене 20 руб. за батон связаны зависимостью у=20х, это прямая пропорциональность, где к=20. 2.Обратимся к движению. От чего зависит путь? ( от скорости и времени движения). Но скорость при равномерном движении остаётся постоянной. Тогда от чего зависит путь? (от времени). Как, зная скорость и время движения, найти путь, пройденный телом? (S=vt) – это тоже прямая пропорциональность, где коэффициент пропорциональности v=s/t. А теперь рассмотрим графики некоторых функций. 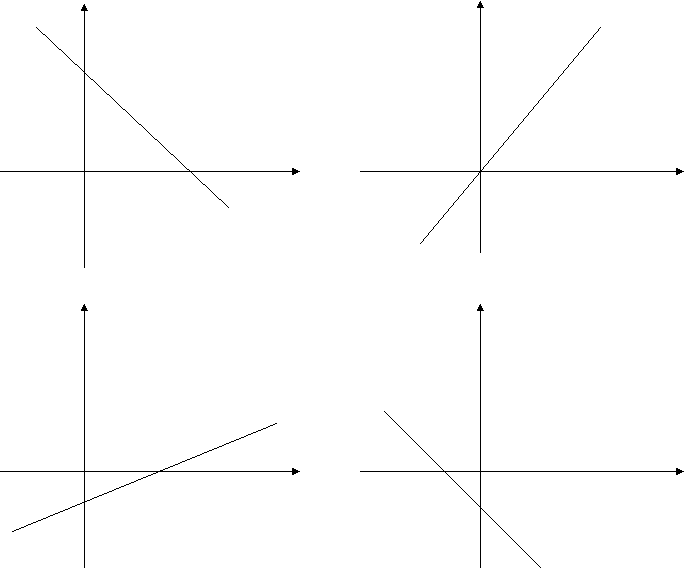 у у у у0 х 0 х График какой функции отличается от других? Чем? (график 2, прямая проходит через начало координат). Графиком прямой пропорциональности у=кх является прямая, проходящая через начало координат. Если к>0, то прямая образует с положительным направлением оси Х острый угол, если к<0, то этот угол тупой. Поэтому к в записи у=кх называют угловым коэффициентом. Задание В уравнении S=3t что означает цифра 3? (скорость) Постройте график этого уравнения. Найдите по графику путь, пройденный за 4 секунды? В конце урока хотелось бы обратиться к народной мудрости. Как известно, пословицы – это отражение устойчивых закономерностей, выверенных многовековым опытом народа. Некоторые пословицы иллюстрируют характерные свойства функций. Например: «Чем дальше в лес, тем больше дров» «Как аукнется, так и откликнется» «Что посеешь, то пожнёшь» «Тише едешь, дальше будешь» Домашнее задание: 1.Придумать задачу из жизни, где применяется прямая пропорциональность. 2.Найти пословицы и поговорки, иллюстрирующие прямую пропорциональность. Список использованной литературы 1. А.Г. Мордкович, Е.Е. Тульчинская. Алгебра 7-9. Тесты. 2.Л.И.Звавич, А.Р.Рязановский. Алгебра-8. Задачник для классов с углубленным изучением математики. 3.Э.Г. Гельфман и др. “Сказка о спящей красавице или ФУНКЦИЯ” Серия математика, психология, интеллект. Изд-во Томского унив., 1996 4. Г.Н. Степанова, А.П. Степанов «Сборник вопросов и задач по физике», Профильная школа. — СПб.: ООО «СТП Школа», 2005. 5.Л. А. Горлова.Интегрированные уроки физики. 7-11 классы Серия: Мастерская учителя физики.Издательство: ВАКО, 2009 г. 6.А. Г. Мордкович: Алгебра. Методическое пособие для учителя. 7-9 классы - Мнемозина, 2004. |