ТРЕБОВАНИЯ К УРОВНЮ
ПОДГОТОВКИ ВЫПУСКНИКОВ
В результате изучения математики ученик должен
знать/понимать1
существо понятия математического доказательства; примеры доказательств;
существо понятия алгоритма; примеры алгоритмов;
как используются математические формулы, уравнения и неравенства; примеры их применения для решения математических и практических задач;
как математически определенные функции могут описывать реальные зависимости; приводить примеры такого описания;
как потребности практики привели математическую науку к необходимости расширения понятия числа;
вероятностный характер многих закономерностей окружающего мира; примеры статистических закономерностей и выводов;
каким образом геометрия возникла из практических задач землемерия; примеры геометрических объектов и утверждений о них, важных для практики;
смысл идеализации, позволяющей решать задачи реальной действительности математическими методами, примеры ошибок, возникающих при идеализации;
Алгебра
уметь
составлять буквенные выражения и формулы по условиям задач; осуществлять в выражениях и формулах числовые подстановки и выполнять соответствующие вычисления, осуществлять подстановку одного выражения в другое; выражать из формул одну переменную через остальные;
выполнять основные действия со степенями с целыми показателями, с многочленами и с алгебраическими дробями; выполнять разложение многочленов на множители; выполнять тождественные преобразования рациональных выражений;
применять свойства арифметических квадратных корней для вычисления значений и преобразований числовых выражений, содержащих квадратные корни;
решать линейные, квадратные уравнения и рациональные уравнения, сводящиеся к ним, системы двух линейных уравнений и несложные нелинейные системы;
решать линейные и квадратные неравенства с одной переменной и их системы;
решать текстовые задачи алгебраическим методом, интерпретировать полученный результат, проводить отбор решений, исходя из формулировки задачи;
изображать числа точками на координатной прямой;
определять координаты точки плоскости, строить точки с заданными координатами; изображать множество решений линейного неравенства;
распознавать арифметические и геометрические прогрессии; решать задачи с применением формулы общего члена и суммы нескольких первых членов;
находить значения функции, заданной формулой, таблицей, графиком по ее аргументу; находить значение аргумента по значению функции, заданной графиком или таблицей;
определять свойства функции по ее графику; применять графические представления при решении уравнений, систем, неравенств;
описывать свойства изученных функций, строить их графики;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
выполнения расчетов по формулам, составления формул, выражающих зависимости между реальными величинами; нахождения нужной формулы в справочных материалах;
моделирования практических ситуаций и исследовании построенных моделей с использованием аппарата алгебры;
описания зависимостей между физическими величинами соответствующими формулами при исследовании несложных практических ситуаций;
интерпретации графиков реальных зависимостей между величинами;
СОДЕРЖАНИЕ ТЕМ УЧЕБНОГО КУРСА
Алгебра 9 класс
1. Квадратичная функция
Функция. Возрастание и убывание функции. Квадратный трехчлен. Разложение квадратного трехчлена на множители. Решение задач путем выделения квадрата двучлена из квадратного трехчлена. Функция y=ax2 + bx + с, её свойства, график. Простейшие преобразования графиков функций. Решение неравенств второй степени с одной переменной. [Решение рациональных неравенств методом интервалов.]
Цель – выработать умение строить график квадратичной функции и применять графические представления для решения неравенств второй степени с одной переменной.
Знать основные свойства функций, уметь находить промежутки знакопостоянства, возрастания, убывания функций
Уметь находить область определения и область значений функции, читать график функции
Уметь решать квадратные уравнения, определять знаки корней
Уметь выполнять разложение квадратного трехчлена на множители
Уметь строить график функции у=ах2 , выполнять простейшие преобразования графиков функций
Уметь строить график квадратичной функции, выполнять простейшие преобразования графиков функций
Уметь строить график квадратичной функции» находить по графику нули функции, промежутки, где функция принимает положительные и отрицательные значения.
Уметь построить график функции y=ax2 и применять её свойства. Уметь построить график функции y=ax2 + bx + с и применять её свойства
Уметь находить токи пересечения графика Квадратичной функции с осями координат. Уметь разложить квадратный трёхчлен на множители.
Уметь решать квадратное уравнение.
Уметь решать квадратное неравенство алгебраическим способом. Уметь решать квадратное неравенство с помощью графика квадратичной функции
Уметь решать квадратное неравенство методом интервалов. Уметь находить множество значений квадратичной функции.
Уметь решать неравенство ах2 +вх+с.≥0 на основе свойств квадратичной функции
2. Уравнения и системы уравнений
Целое уравнение и его корни. Решение уравнений третьей и четвертой степени с одним неизвестным с помощью разложения на множители и введения вспомогательной переменной.
Уравнение с двумя переменными и его график. Уравнение окружности. Решение систем, содержащих одно уравнение первой, а другое второй степени. Решение задач методом составления систем. Решение систем двух уравнений второй степени с двумя переменными.
Цель – выработать умение решать простейшие системы, содержащие уравнения второй степени с двумя переменными, и решать текстовые задачи с помощью составления таких систем.
Знать методы решения уравнений:
а) разложение на множители;
б) введение новой переменной;
в)графический способ.
Уметь решать целые уравнения методом введения новой переменной
Уметь решать системы 2 уравнений с 2 переменными графическим способом
Уметь решать уравнения с 2 переменными способом подстановки и сложения
Уметь решать задачи «на работу», «на движение» и другие составлением систем уравнений.
3. Прогрессии
Арифметическая и геометрическая прогрессии. Формулы n-го члена и суммы n первых членов прогрессии.
Цель – дать понятие об арифметической и геометрической прогрессиях как числовых последовательностях особого вида.
Добиться понимания терминов «член последовательности», «номер члена последовательности», «формула n –го члена арифметической прогрессии»
Знать формулу n –го члена арифметической прогрессии, свойства членов арифметической прогрессии, способы задания арифметической прогрессии
Уметь применять формулу суммы n –первых членов арифметической прогрессии при решении задач
Знать, какая последовательность является геометрической, уметь выявлять, является ли последовательность геометрической, если да, то находить q
Уметь вычислять любой член геометрической прогрессии по формуле, знать свойства членов геометрической прогрессии
Уметь применять формулу при решении стандартных задач
Уметь применять формулу S=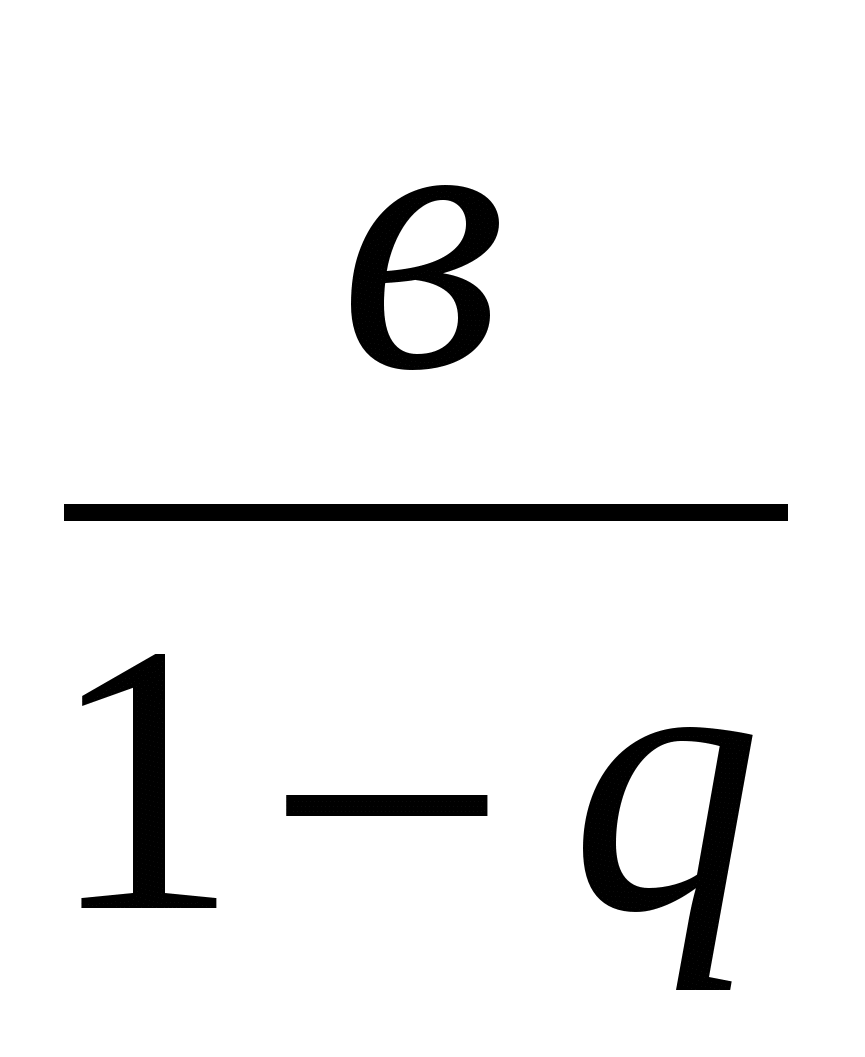 при решении практических задач при решении практических задач
Уметь находить разность арифметической прогрессии
Уметь находить сумму n первых членов арифметической прогрессии. Уметь находить
любой член геометрической прогрессии. Уметь
находить сумму n первых членов геометрической
прогрессии. Уметь решать задачи.
4. Степенная функция. Корень n-й степени
Четная и нечетная функции. Функция y=xn, Определение корня n-й степени.
Цель – ввести понятие корня n-й степени.
Знать определение и свойства четной и нечетной функций
Уметь строить график функции у=хn , знать свойства степенной функции с натуральным показателем, уметь решать уравнения хn=а при: а) четных и б)нечетных значениях n
Знать определение корня n- й степени, при каких значениях а имеет смысл выражение 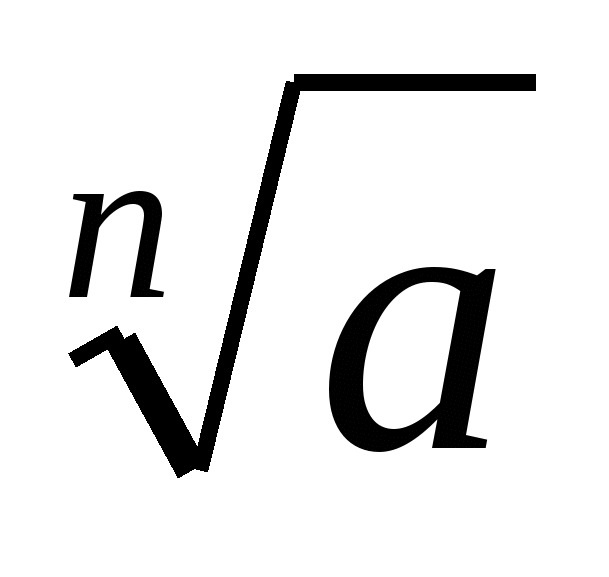
Уметь выполнять простейшие преобразования и вычисления выражений, содержащих корни, применяя изученные свойства арифметического корня n-й степени
Знать, что степень с основанием, равным 0 определяется только для положительного дробного показателя и знать, что степени с дробным показателем не зависят от способа записи r в виде дроби
Знать свойства степеней с рациональным показателем, уметь выполнять простейшие преобразования выражений, содержащих степени с дробным показателем
Уметь выполнять преобразования выражений, содержащих степени с дробным показателем
5. Элементы статистики и теории вероятностей
Комбинаторные задачи. Перестановки, размещения, сочетания. Перестановки. Размещения. Сочетания Вероятность случайного события
Знать формулы числа перестановок, размещений, сочетаний и уметь пользоваться ими.
Уметь пользоваться формулой комбинаторики при вычислении вероятностей
6. Тригонометрические выражения
Радианное измерение углов. Синус, косинус, тангенс и котангенс произвольного угла. Основные тригонометрические тождества 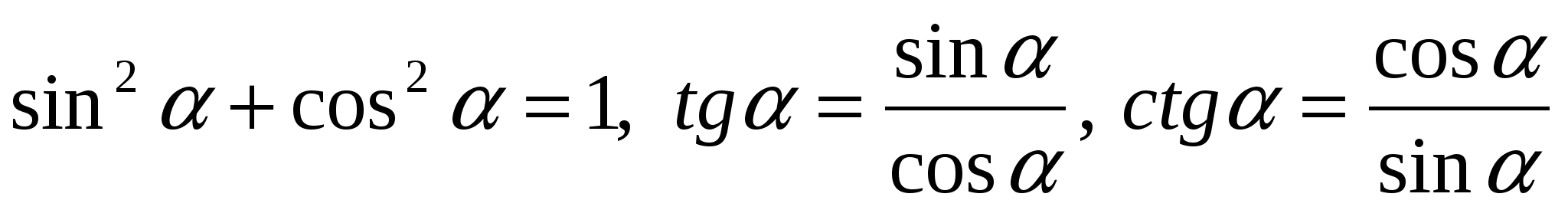 . Их применение в вычислениях и тождественных преобразованиях. . Их применение в вычислениях и тождественных преобразованиях.
Цель – ввести понятия синуса, косинуса, тангенса и котангенса произвольного угла; сформировать умения вычислять значения тригонометрических функций по известному значению одной из них; выполнять несложные преобразования тригонометрических выражений.
Знать определение тригонометрических функций, область определения и область значений, уметь их находить
Знать свойства тригонометрических функций и что при изменении угла на целое число оборотов значения синуса, косинуса, тангенса и котангенса не изменяются
Знать приближенное значение 1 радиана в градусах, уметь переводить радианную меру угла в градусную и наоборот
Уметь применять основные тригонометрические формулы одного и того же угла к преобразованию выражений
Уметь применять изученные формулы к преобразованию выражений
7. Повторение. Решение задач
Закрепление знаний, умений и навыков, полученных на уроках по данным темам (курс алгебры 9 класса).
Геометрия 9 класс
Тема
|
Знания, умения, навыки учащихся
|
Векторы
|
|
Понятие вектора
|
Уметь изображать и обозначать векторы, откладывать от любой точки плоскости вектор, равный данному
|
Сложение и вычитание векторов
|
Знать законы сложения векторов, уметь строить сумму двух и более векторов, пользоваться правилом треугольника, параллелограмма, многоугольника
|
Умножение векторов на число и его свойства
|
Знать свойства умножения вектора на число, уметь решать задачи типа 782-787
|
Применение векторов к решению задач
Средняя линия трапеции
|
Знать, какой отрезок называется средней линией трапеции; уметь формулировать и доказывать теорему о средней линии трапеции; уметь решать задачи типа 793-798
|
Метод координат
|
|
Разложение вектора по 2 неколлинеарным векторам. Координаты вектора
|
Уметь применять теорему о разложении вектора по 2 неколлинеарным векторам, знать правила действий над векторами с заданными координатами.
|
Простейшие задачи в координатах
|
Уметь выводить формулы координат вектора через координаты его конца и начала координат середины отрезка, длины вектора и расстояния между двумя точками, уметь решать задачи типа 945, 951
|
Уравнение окружности
Уравнение прямой
|
Знать и уметь выводить уравнения окружности и прямой, уметь строить окружность и прямые, заданные уравнениями решать задачи типа 966, 972
|
Соотношения между сторонами и углами треугольника
|
|
Синус, косинус, тангенс
|
Знать, как вычисляется синус, косинус, тангенс для углов от 0 до 180, уметь доказывать основное тригонометрическое тождество, знать формулу для вычисления координат точки, уметь решать задачи типа 1013-1019
|
Основное тригонометрическое тождество
|
Формулы для вычисления координат точки
|
Теорема о площади круга
|
Уметь доказывать теорему о площади треугольника, теорему синусов, теорему косинусов; применять эти теоремы при решении задач
|
Теорема синусов
|
Теорема косинусов
|
Решение треугольников
|
Скалярное произведение векторов
|
Знать определение скалярного произведения векторов, условие перпендикулярности векторов, выражать скалярное произведение в координатах , знать его свойства, уметь решать задачи типа 1044, 1045, 1047, 1048,1050, 1051
|
Длина окружности и площадь круга
|
|
Правильный многоугольник.
Окружность, около правильного многоугольника
|
Знать определение правильного многоугольника, теорему об окружности, описанной около правильного многоугольника и окружности, вписанной в правильный многоугольник; знать формулы для вычисления угла, площади и стороны правильного многоугольника и радиуса вписанной в него окружности, уметь их выводить и применять при решении задач типа 1081, 1083,1087, 1094, 1098, 1100
|
Окружность, вписанная в правильный многоугольник
|
Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной окружности
|
Длина окружности
|
Знать формулы длины окружности и дуги окружности, уметь применять их при решении и задач типа 1111,1113, 1119; знать формулы площади круга и кругового сектора, уметь применять их при решении задач типа 1120, 1126, 1127
|
Площадь круга. Площадь кругового сектора
|
Движения
|
|
Понятие движения
|
Уметь объяснять, что такое отображение плоскости на себя, знать определение движения плоскости, уметь доказывать, что осевая и центральная симметрии являются движениями и что при движении отрезок отображается на отрезок, а треугольник на равный ему треугольник, решать задачи типа 1152, 1159, 1161
|
Параллельный перенос
|
Уметь объяснять, что такое параллельный перенос и поворот, доказывать, что параллельный перенос и поворот являются движениями плоскости; решать задачи типа 1164, 1165, 1167, 1168
|
Поворот
|
ТЕМАТИЧЕСКИЙ ПЛАН
к курсу АЛГЕБРЫ 9 класса
№
п/п
|
Название темы
|
Кол-во
часов
|
Контрольные
работы
|
1
|
Неравенства и системы неравенств
|
16
|
1
|
2
|
Системы уравнений
|
15
|
1
|
3
|
Числовые функции
|
25
|
2
|
4
|
Прогрессии
|
16
|
1
|
5
|
Элементы комбинаторики, статистики и теории вероятностей
|
12
|
1
|
6.
|
Итоговое повторение
|
18
|
1
|
7.
|
Резерв
|
5
|
|
итого 107 7
ТЕМАТИЧЕСКИЙ ПЛАН
к курсу ГЕОМЕТРИИ 9 класса
№ п/п
|
Название темы
|
Всего часов
|
Контрольные
работы
|
1
|
Векторы
|
6
|
|
2
|
Метод координат
|
7
|
1
|
3
|
Соотношения между сторонами и углами треугольника
|
14
|
1
|
4
|
Длина окружности и площадь круга
|
9
|
1
|
5
|
Движения
|
6
|
1
|
6
7
|
Начальные сведения из стереометрии
Повторение
|
11
15
|
1
|
итого 68 5
|
 Скачать 0.75 Mb.
Скачать 0.75 Mb.