|
Разложение многочлена на множители с помощью комбинации различных приёмов
«Разработка плана-конспекта урока и учебных материалов в среде SMART Notebook по математике для 7 класса по теме: «Разложение многочлена на множители с помощью комбинации различных приёмов»
Выполнила:
Горячева Ольга Васильевна,
учитель математики ГБОУ СОЛ
Промышленного р-на г.Самара
Самара ,2015г.
Технологическая карта урока
1.Тема урока: «Разложение многочлена на множители с помощью комбинации различных приёмов». Урок развивающего контроля, 1 час.
2. Разработка урока соответствует программе по математике Министерства Образования РФ.
3. Учебник «Алгебра-7» под.ред. А.Г.Мордковича, изд.»Мнемозина», М.,2007, дидактические материалы, тесты, дополнительная литература.
4. Цель урока:
Создать содержательные и организационные условия для самостоятельного применения обучающимися комплекса знаний и способов деятельности по теме «Разложение многочлена на множители с помощью комбинации различных приёмов».
5. Задачи:
Образовательная: выявить уровень овладения обучающимися комплекса знаний и умений по заданной теме, применения навыков разложения многочлена на множители разными способами при выполнении заданий базового уровня и заданий повышенной сложности.
Развивающая: развивать навыки самоконтроля при выполнении заданий на применение правил разложения многочлена на множители, развивать логическое мышление, быстроту реакции, умение преодолевать трудности для достижения намеченной цели.
Воспитательная: воспитывать положительное отношение к знаниям, прививать интерес к математике, формировать навыки самоорганизации и самоконтроля, помочь обучающимся осознать ценность совместной деятельности.
Урок предусматривает соблюдение дидактических, гигиенических, психологических требований.
6. Тип урока: урок развивающего контроля комплексного применения соответствующих способов деятельности.
7. Формы работы: фронтальная, работа в парах, работа в группах, диалоговая беседа.
8 .Техническое оборудование: интерактивная доска SMART Notebook, компьютеры, тесты.
9. Планируемые результаты:
предметные – проведение анализа ситуаций, структурирование и
систематизация знаний, закрепление символьной записи;
личностные - развитие креативности мышления, грамотное изложение мысли
устной и письменной форме, контроль процесса учебной
деятельности ;
метапредметные – видение математической задачи в контексте проблемной си-
туации, окружающем мире, использование интерактивной доски, составление алгоритма для решения задач.
Ход урока
1
|
Подготовка к уроку
|
Использование учебников, дидактических материалов по алгебре, интернет-ресурсов, средств интерактивной доски
|
2
|
Основные этапы урока
|
1.Повторение основных определений с помощью средств интерактивной доски.
2.Проверка навыков решения задач по готовым ответам с использованием средств интерактивной доски.
3.Работа в парах с элементами взаимопроверки, проверки ответов на интерактивной доске.
4.Работа в группах по решению задач с последующей проверкой ответов на интерактивной доске.
5.Решение уравнений на заданную тему.
6.Рефлексия.
|
3
|
Главная цель учителя на уроке
|
Организовать деятельность учащихся по выбору решений в парах и группах, обобщению способов действий, систематизации результатов.
|
4
|
Формулирование заданий для учащихся
|
1.Обобщить разные методы разложения многочлена на множители.
2.Создать типовые модели решения задач на разложение многочленов.
3.Обобщить и проанализировать решения задач в группах, защитить решения.
4.Выбрать способы решения уравнений и придумать подобные для домашней работы.
|
5
|
Форма урока
|
Индивидуальная работа, работа в парах, группах.
|
6
|
Нестандартность ведения урока
|
Использование средств интерактивной доски для закрепления материала и проверки решений.
|
7
|
Образовательная среда
|
Оформление класса, подготовка программы интерактивной доски, карточки с заданиями по вариантам, оценочные листы учащихся.
|
8
|
Результаты обучения
|
Обобщение, закрепление знаний по теме «Разложение многочлена на множители с помощью комбинации различных приёмов», развитие межпредметных связей, коммуникативной комтетенции, развитие способности самооценки, учёт динамики промежуточных результатов.
|
Этапы организации учебной деятельности
|
Цель этапа
|
Содержание педагогического взаимодействия
|
Деятельность учителя
|
Деятельность обучающихся
|
Познавательная
|
Коммуникативная
|
Регулятивная
|
1.Постановка учебной задачи
|
Систематизация знаний и умений учащихся в области методов разложения многочлена на множители
|
Организация погружения обучающихся в проблему структурирования знаний
|
Повторение разных известных способов разложения многочлена на множители
|
Совместная деятельность в парах и группах
|
Сохранение учебной задачи
|
2.Совместное исследование проблемы
|
Поиск решения учебной задачи по систематизации знаний
|
Организация процесса повторения, создания модели. Организация обсуждения хода решения
|
Анализ индивидуальной деятельности, доказательство и защита представленных решений
|
Осознанные приёмы речи при анализе задач
|
Обсуждение предметных способов решения
|
3.Моделирование
|
Фиксация модели решения стандартной задачи
|
Организация учебного взаимодействия учеников в паре, группе
|
Аналитическая запись решения задачи
|
Восприятие ответов обучающихся
|
Осуществление самоконтроля и взаимоконтроля
|
4.Конструирование способа действия при решении задач
|
Построение ориентированного способа действия
|
Организация учебного исследования при решении задач
|
Проведение комплексного исследования
|
Обсуждение содержания полученного решения
|
Осуществление контроля в группах
|
5.Решение разных уравнений
|
Коррекция отработки действия созданной модели
|
Организация самостоятельной практической деятельности учащихся
|
Отработка методов систематизации применительно к новым начальным условиям
|
Обучение способам формулировать своё мнение и отстаивать свою позицию
|
Осуществление пошагового контроля
|
6.Применение закреплённых методов
|
Отработка способов в новой поставленной задаче
|
Организация самостоятельной деятельности учащихся
|
Применение отработанного способа в условиях новой поставленной задачи
|
Использование речи в регуляции деятельности развития межпредметных связей
|
Организация самоконтроля
|
7.Контроль на этапе окончания работы
|
Контроль
|
Организация контрольно-оценивающей деятельности учащихся
|
Оценивание результатов деятельности на уроке и по окончании темы
|
Рефлексия своей деятельности
|
Осуществление контроля по результату
|
Задания на разложение многочлена на множители по рядам
1 ряд 2 ряд 3 ряд
1) 3a +12b 1)16a2 + 8ab + b2 1)10a + 15c
2) 2a+ 2b + a2 + ab 2)3m – 3n + mn – n2 2)4a2 – 9b2
3) 9a2 – 16b2 3)5a -25b 3)6xy – ab – 2bx – 3ay
4) 7a3b – 14ab2 + 7ab 4)4a2 – 3ab + a – aq + 3bq – q 4)4a2 + 28ab + 49b2
5) m2 +mn – m – mq – nq + qм 5)9a2 – 30ab + 25b2 5)b(a + c) + 2a + 2c
6) 4a2 – 4ab + b2 6)2(a2 + 3bc) +a(3b +4c) 6)5a3c – 20acb – 10ac
7) 2 (3a2 + bc) + a (4b +3c) 7)144a2 – 25b2 7)x2 -3x -5x + 15
8) 25a2 + 70ab +49b2 8)9a3b – 18ab2 – ab2 8)9a2 – 6ac + c2
Ответы на задания по рядам проверяются по таблице на доске
Соответствие слайдов презентации, составленной посредством программы интерактивной доски SMART Notebook, этапам урока математики для 7 класса по теме «Разложение многочлена на множители с помощью комбинации различных приёмов»
Учитель ГБОУ СОЛ ГорячеваО.В.
1 этап. Повторение основных определений и способов разложения многочлена на множители (фронтальная работа).
Слайд 1. Определение разложения на множители. Определения на доске закрыты шторкой. После того, как ученики ответили, открывается шторка и выбирается правильный ответ. Путем нажатия на доску между вопросом и правильным ответом проявляется соединительная линия.
Слайд 2. Ученикам предлагается уточнить определение способа вынесения общего множителя за скобку. Правильный ответ появляется после нажатия на доску ниже вопроса.
Слайд 3.Повторение формул сокращенного умножения как средства разложения многочлена на множители. После нажатия на все объекты (заголовок, стрелки, формулы) происходит увеличение всех объектов.
Слайд 4. Повторение схемы разложения на множители способом группировки. Щелчком на доске поворачивается квадрат с заданием, путем нажатия на доску появляются нужные соединительные линии.
2, 3 этапы. Решение задач на использование разных методов разложения многочлена на множители.
Слайд 5. Ученикам в парах предлагается решить задачи, проверить решения друг друга. Разные учащиеся на доске перемещают формулы в соответствующие колонки.
Слайд 6. Решение задач индивидуально. На доске ответы перемещаются и группируются в правильные колонки.
4, 5 этапы. Решение задач, уравнений по рядам и самостоятельно.
Слайд 7. Проверка ответов на доске путем открывания шторок в таблице.
6 этап. Рефлексия. После решения всех задач, выставления оценок и выдачи домашнего задания ученикам предоставляется возможность оценить свою деятельность на уроке.
Слайд 8. Оценка собственной деятельности учащимися: «устал, было нелегко» или «легко двигался вперёд».
Решить задачи и с помощью интерактивной доски проверить соответствие разложения многочленов способам разложения на множители
I вариант II вариант
20x3y2 + 4x2y
15a3b + 3a2b3
Вынесение общего множителя за скобки
4a2 – 5a + 9
9x2 + 5x + 4
2bx – 3ay – 6by + ax
2an – 5bm – 10bn + am
Формула сокращенного умножения
a4 – b8
x2 + 6x + 9
9x2 + y4
4a4 + 25b2
Не раскладывается на множители
 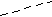
27b3 + a6
49m4 – 25n2
a2 + ab – 5a – 5b
3a2 + 3ab – 7a – 7b
Способ группировки
 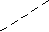
b (a + 5) – c (a +5)
2y (x – 5) + x (x – 5)
Метод разложения на множители
Вынесение общего множителя за скобки
Формулы сокращенного умножения
Способ
группировки
20x3y2 + 4x2y
a4 – b8
2bx – 3ay – 6by + ax
b (a + 5) – c (a +5)
27b3 + a6
a2 + ab – 5a – 5b
15a3b + 3a2b3
x2 + 6x + 9
2an – 5bm – 10bn + am
2y (x – 5) + x (x – 5)
49m4 – 25n2
3a2 + 3ab – 7a – 7b
|
|
|
|
|
|
|
|
|
|
|
|
Решить уравнения
а) x2 – 15x + 56 = 0 б) x2 + 10x + 21 = 0
Решение: Решение:
x2 – 7x – 8x + 56 = 0 x2 + 10x + 25 – 4 = 0
(x2 – 7x) – (8x – 56) = 0 (x + 5)2 – 4 = 0
x (x – 7) – 8 (x – 7) =0 (x + 5 – 2) (x + 5 + 2)=0
(x – 7) (x – 8) = 0 (x + 3) (x + 7) = 0
x – 7 = 0 или x – 8 = 0, x + 3 = 0 или x + 7 =0 ,
x = 7 или x = 8 x = -3 или x = -7
|
Задания с взаимопроверкой
Вариант 1 Вариант 2
1. 5a3 – 125ab2 1. 63ab3 – 7a2b
2. a2 – 2ab + b2 – ac + bc 2. M2 + 6mn + 9n2 – m – 3n
3. (c – a) (c + a) – b (b – 2a) 3. (b – c) (b + c) – a (a + 2c)
4. x2 – 3x + 2 4. x2 + 4x + 3
5. x4 + 5x2 + 9 5. X3 + 3x2 + 4
Ответы:
1. 5a (a – 5b) (a + 5b) 1. 7ab (9b2 – a)
2. (a- b) (a – b – c) 2. (m + 3n) (m + 3n – 1)
3. (c – a +b) (c + a – b) 3. (b + a + c) (b – a – c)
4. (x – 2) (x – 1) 4. (x + 3) (x + 1)
5. (x2 + 3 – x) (x2 + 3 + x) 5. (x2 + 2 – x)(x2 + 2 + x)
|
Д/з
№№1058(б,в),1063(а,г),1066(а,б),1070,1072(а)
|
Рефлексия
|
|
|
|
| |
|
|
 Скачать 111.47 Kb.
Скачать 111.47 Kb.