Протокол №1 от «24» августа 2012 г. Руководитель методобъединения И. М. Мамеева-Шварцман «Согласовано»

Название	Протокол №1 от «24» августа 2012 г. Руководитель методобъединения И. М. Мамеева-Шварцман «Согласовано»
страница	4/5
Дата	12.03.2016
Размер	0.75 Mb.
Тип	Протокол

1 2 3 4 5


	а	Решение задач «Функция 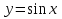, её свойства и график»	§ 10	Р	ЗИ	ВП
	а	Функция 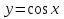, её свойства и график	§ 11	ПП	ОНМ	ФО
	а	Решение задач «Функция 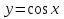, её свойства и график»	§ 11	ТР Р	ЗИ	РП
	а	Периодичность функций 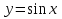,	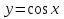§ 12	ПП	К	СП
	а	Как построить график функции y =mf(x), если известен график функции y = f(x)	§ 13	ПП	ОНМ	ФО
	а	Как построить график функции y = f(kx), если известен график функции y = f(x)	§ 13		К	ПДЗ
	а	Функции y = tg x, y = ctg x, их свойства и графики	§ 14		К	УО
	а	Решение задач «Функции y = tg x, y = ctg x, их свойства и графики»	§ 14	Р	ПЗУ	РК
	а	Контрольная работа № 3 «Свойства и графики тригонометрических функций»	§§ 10-14	ТР, Р	ПКЗУ	КР
Глава I. Параллельность прямых и плоскостей – 16 ч
	г	Параллельные прямые в пространстве	п.4-5		УЛ, ДМ, ЧИИ, НП, ДКИМ	ПП, ИР	Знают определение параллельных прямых в пространстве, формулировки основных теорем о параллельности прямых, умеют их доказывать и распознавать в конкретных условиях, применять теоремы к решению задач Знают определение параллельных прямых в пространстве, формулировки основных теорем о параллельности прямых, умеют их доказывать и распознавать в конкретных условиях, применять теоремы к решению задач Знают определение параллельных прямых в пространстве, формулировки основных теорем о параллельности прямых, умеют их доказывать и распознавать в конкретных условиях, применять теоремы к решению задач Знают определение параллельных прямых в пространстве, формулировки основных теорем о параллельности прямых, умеют их доказывать и распознавать в конкретных условиях, применять теоремы к решению задач Могут различать пересекающиеся, параллельные и скрещивающиеся прямые; угол между прямыми в пространстве. Владение навыками контроля и оценки своей деятельности, умением предвидеть возможные последствия своих действий.	К	УО
	г	Параллельность прямой и плоскости	п.6			ИР		К	УО
	г	Решение задач «Параллельность прямой и плоскости»	п.4-6			Р,ПП		ПЗУ	ВП
	г	Параллельность прямой и плоскости вокруг нас	п.4-6			ПП		К	ВП
	г	Скрещивающиеся прямые	п.7			ИР, Р			УО
	г	Углы с сонаправленными сторонами	п.8-9			ИР, Р			УО
	г	Угол между прямыми	п.8-9			ИР, Р			ВП
	г	Взаимное расположение прямых и плоскостей в пространстве Контрольная работа № 4 «Параллельность прямых, прямой и плоскости» (20 мин)	п.4-9			ПП, Р ТР		К ПКЗУ	УО КР
	г	Параллельность плоскостей	п.10			ИР, Р	Могут различать пересекающиеся, параллельные и скрещивающиеся прямые; угол между прямыми в пространстве. Могут найти и устранить причины возникших трудностей Знают определение и признаки параллельности плоскостей. Поиск нескольких способов решения, аргументация рационального способа, проведение доказательных рассуждений. Знают определение и признаки параллельности плоскостей. Могут самостоятельно искать, и отбирать необходимую для решения учебных задач информацию Могут отличать тетраэдр от других видов пространственных тел. Знают определение тетраэдра, всех его элементов. Могут излагать информацию, интерпретируя факты, разъясняя значение и смысл теории. Могут отличать тетраэдр от других видов пространственных тел. Знают определение тетраэдра, всех его элементов. Осуществляют проверку выводов, положений, закономерностей, теорем. Могут узнавать параллелепипед среди множества многогранников, знают определение параллелепипеда, основных его элементов, знать свойства параллелепипеда. Умеют проводить самооценку собственных действий. Могут узнавать параллелепипед среди множества многогранников, знают определение параллелепипеда, основных его элементов, знать свойства параллелепипеда. Восприятие устной речи, участие в диалоге, запись главного, приведение примеров. Учащихся демонстрируют: понимания основных элементов стереометрии, пространственных фигур, параллельности прямых в пространстве, параллельности прямой и плоскости; параллельности двух плоскостей Учащихся демонстрируют: понимания основных элементов стереометрии, пространственных фигур, параллельности прямых в пространстве, параллельности прямой и плоскости; параллельности двух плоскостей.	К	ПДЗ
	г	Свойства параллельных плоскостей	п.11			ИР			ФО
	г	Тетраэдр	п.12			ИР			СП
	г	Параллелепипед	п.13			ИР, ПП			УО
	г	Задачи на построение сечений	п.14			ПП, Р			ПДЗ
	г	Свойства параллелепипеда	п.12-14			ИР, ПП			ВП
	г	Контрольная работа № 5 «Параллельность плоскостей»	п.12-14			ТР, Р		ПКЗУ	КР
	г	Зачёт № 1 «Параллельность прямых и плоскостей»	п.12-14			ТР, Р		ПКЗУ	З, ИО
Глава 3. Тригонометрические уравнения - 10 ч
	а	Первые представления о решении простейших тригонометрических уравнений. Арккосинус	Гл.3,§15		СУЛ, ДМ, ДКИМ, ЧИИ, НП, ТК	ИР, Р	Знать определение арккосинуса. – извлекать необходимую информацию из учебно-научных текстов; – воспринимать устную речь, участвовать в диалоге, Уметь: – решать простейшие уравнения сos t = a; Знать определение арксинуса. Уметь:– передавать информацию сжато, полно, выборочно; – отражать в письменной форме свои решения, рассуждать и обобщать,участвовать в диалоге, выступать с решением проблемы; Знать определение арксинуса. Уметь: – решать простейшие уравнения sin t = a; – извлекать необходимую информацию из учебно-научных текстов; – подбирать аргументы, соответствующие решению, участвовать в диалоге. Знать определение арктангенса, арккотангенса. Уметь: – решать простейшие уравнения tg t = a и ctg t = a; – обосновывать суждения, давать определения, приводить доказательства, примеры. Уметь: – решать простейшие тригонометрические уравнения по формулам; – обосновывать суждения, давать определения, приводить доказательства, примеры;– излагать информацию, обосновывая свой собственный подход. Уметь: – решать тригонометрические уравнения методом замены переменной, методом разложения на множители; – участвовать в диалоге, понимать точку зрения собеседника, признавать право на иное мнение. – владеть навыками самоанализа и самоконтроля	К	УО
	а	Решение уравнения	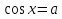§ 15			ИР, Р		ОНМ	ПДЗ
	а	Арксинус	§ 16			ИР		ОНМ	ФО
	а	Решение уравнения	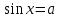§ 16			ТР		ЗИ	ПР
	а	Арктангенс и арккотангенс. Решение уравнений tg x = a, ctg x = a	§ 17			ИР, ТР		К	СП
	а	Простейшие тригонометрические уравнения	§ 18 п. 1			ПП ИР Р		К	УО
	а	Два основных метода решения тригонометрических уравнений	§ 18 п. 2			ПП ИР Р		К	ПДЗ
	а	Однородные тригонометрические уравнения	§ 18 п. 3			ИР, ТР		К	ВП
	а	Решение тригонометрических уравнений	§ 18			Р, ТР		ПЗУ	РК
	а	Контрольная работа № 6 «Тригонометрические уравнения»	§§ 15-18			Р, ТР		ПКЗУ	КР
Глава II. Перпендикулярность прямых и плоскостей – 17 ч
	г	Перпендикулярные прямые в пространстве	п.15-16		СУЛ, ДМ, ДКИМ, ЧИИ	ИР	Могут найти угол между прямыми различно расположенных в пространстве. Могут выделить и записать главное, могут привести примеры. Знают признак перпендикулярности прямой и плоскости; понятие ортогональное проектирование. Умеют добывать информацию по заданной теме в источниках различного типа. Знают признак перпендикулярности прямой и плоскости; понятие ортогональное проектирование. Умеют пользоваться энциклопедией, математическим справочником, записанными правилами. Знают понятие перпендикуляр и наклонная; теорему о трех перпендикулярах. Восприятие устной речи, участие в диалоге, понимание точки зрения собеседника. Знают признак перпендикулярности прямой и плоскости; понятие ортогональное проектирование. Умеют пользоваться энциклопедией, математическим справочником, записанными правилами. Умеют находить расстояние от точки до прямой. Знают понятие перпендикуляр и наклонная; теорему о трех перпендикулярах. Восприятие устной речи, проведение информационно-смыслового анализа текста и лекции, приведение и разбор примеров. Знают понятие перпендикуляр и наклонная; теорему о трех перпендикулярах. Участие в диалоге, отражение в письменной форме своих решений, работа с математическим справочником, Знают понятие двугранный угол; признак перпендикулярности двух плоскостей. Формировать умение выбрать и выполнить задание по своим силам и знаниям, применить знания для решения практ. задач. Знают понятие двугранный угол; признак перпендикулярности двух плоскостей. Восприятие устной речи, участие в диалоге, умеют аргументировано отвечать, приведение примеров. Знают понятие перпендикуляр и наклонная; теорему о трех перпендикулярах. Восприятие устной речи, участие в диалоге, понимание точки зрения собеседника. Знают понятие перпендикуляр и наклонная; теорему о трех перпендикулярах. Проведение информационно-смыслового анализа текста, выбор главного и основного. Учащихся демонстрируют: систематические сведения о перпендикулярности прямых и плоскостей в пространстве, обобщают и систематизируют знания о перпендикулярности прямых, перпендикуляре и наклонных, известные им из курса планиметрии. Учащихся обобщают и систематизируют знания о перпендикулярности прямых, перпендикуляре и наклонных, известные им из курса планиметрии. – владеть навыками самоанализа и самоконтроля	К	ПДЗ
	г	Параллельные прямые, перпендикулярные к плоскости	п.15-16			Р			ВП
	г	Признак перпендикулярности прямой и плоскости	п.17			ИР			ФО
	г	Теорема о прямой, перпендикулярной к плоскости	п.18			ИР Р		К	ПДЗ
	г	Перпендикулярность прямой и плоскости	§ 1, с.34-38			ИР		ОНМ	ФО
	г	Расстояние от точки до плоскости	п.19-20			ИР, ПП		К	СП
	г	Теорема о трёх перпендикулярах	п.19-20					К	УО
	г	Применение теоремы о трёх перпендикулярах	п.21					ОНМ	ВП
	г	Решение задач «Применение теоремы о трёх перпендикулярах»	п.21			Р		ЗИ	ФО
	г	Угол между прямой и плоскостью	§ 2			ИР		ОНМ	ПДЗ
	г	Решение задач «Угол между прямой и плоскостью»	§ 2			Р		ЗИ	ФО
	г	Двугранный угол	п.22		СУЛ, ДМ, ДКИМ, ЧИИ	ИР		ОНМ	ПДЗ
	г	Признак перпендикулярности двух плоскостей	п.23			ИР		ОНМ	ПДЗ
	г	Прямоугольный параллелепипед	п.24			ИР		ОНМ	ПДЗ
	г	Перпендикулярность прямых и плоскостей	Гл.2			ИР		ОНМ	ПДЗ
	г	Контрольная работа № 7 «Перпендикулярность прямых и плоскости»	Гл.2			Р, ТР		ПКЗУ	КР
	г	Зачёт № 2 «Перпендикулярность прямых и плоскости»	Гл.2					ПКЗУ	З, ИО
Глава 4. Преобразование тригонометрических выражений – 15 ч
	а	Синус и косинус суммы аргументов	§ 19		УЛ, ДМ, ДКИМ	ИР	Знать формулу синуса, косинуса суммы углов. Уметь: – преобразовывать простейшие выражения, используя основные тождества, формулы приведения; – передавать информацию сжато, полно, выборочно; – участвовать в диалоге, понимать точку зрения собеседника, признавать право на иное мнение Знать формулу синуса, косинуса суммы двух углов. Уметь: –преобразовывать простейшие выражения, используя основные тождества, формулы приведения; – извлекать необходимую информацию из учебно-научных текстов; – выделить и записать главное, привести примеры Знать формулу тангенса и котангенса суммы и разности двух углов. Уметь: – преобразовывать простые тригонометрические выражения; – составлять текст научного стиля; – воспроизводить правила и примеры, работать по заданному алгоритму Знать формулы двойного угла синуса, косинуса и тангенса. Уметь: – применять формулы для упрощения выражений; – объяснить изученные положения на самостоятельно подобранных конкретных примерах Знать формулы двойного угла синуса, косинуса и тангенса. Уметь: – применять формулы для упрощения выражений; – обосновывать суждения, давать определения, приводить доказательства, примеры Знать формулы понижения степени синуса, косинуса и тангенса. Уметь: – применять формулы для упрощения выражений; – использовать для решения познавательных задач справочную литературу Уметь: – преобразовывать суммы тригонометрических функций в произведение; простые тригонометрические выражения; – обосновывать суждения, давать определения, приводить доказательства, примеры Знать, как преобразовывать произведения тригонометрических функций в сумму; преобразования простейших тригонометрических выражений. Уметь развернуто обосновывать суждения Знать формулу перехода от суммы двух функций с различными коэффициентами в одну из тригонометрических функций. Уметь обосновывать суждения, давать определения, приводить доказательства, примеры Уметь: – расширять и обобщать сведения о преобразовании тригонометрических выражений, применяя различные формулы; – владеть навыками контроля и оценки своей деятельности	К	УО
	а	Решение задач «Синус и косинус суммы аргументов»				ТР		ЗИ	РК
	а	Синус и косинус разности аргументов				ИР		ОНМ	ПДЗ
	а	Решение задач «Синус и косинус разности аргументов»				ТР		ЗИ	ВП
	а	Тангенс суммы и разности аргументов	§ 20			ИР		ОНМ	ФО
	а	Решение задач «Тангенс суммы и разности аргументов»	§ 20			ТР		ЗИ	СП
	а	Формулы двойного аргумента	§ 21		СУЛ, ДМ, ДКИМ, НП	ИР		К	УО
	а	Решение задач «Формулы двойного аргумента»				ТР		ЗИ	ПР
	а	Формулы понижения степени				ИР, ТР			РК
	а	Преобразование сумм тригонометрических функций в произведения. Сумма и разность синусов	§ 22					К	ФО
	а	Сумма и разность косинусов						К	ВП
	а	Преобразование выражения A sin x + B cos x к виду C sin (x + t)							УО
	а	Контрольная работа № 8 «Преобразование тригонометрических выражений»	§§ 19-22		ДКИМ	Р, ТР		ПКЗУ	КР
	а	Преобразование произведений тригонометрических функций в суммы	§ 23					К	ПДЗ
	а	Решение задач на преобразование произведений тригонометрических функций в суммы	§ 23					ПЗУ	РК
Глава III. Многогранники – 14 ч
	г	Понятие многогранника	Гл.3, §1		ЧИИ РТ ДМ КИМ	ИР, Р	Знают, как распознавать на чертежах и моделях пространственные формы. Умеют соотносить трехмерные объекты с их описаниями, изображениями. Могут рассуждать, обобщать, аргументировать решение и ошибки, участие в диалоге Имеют представление о многогранниках, различают виды многогранников, знают определение призмы, ее элементов, различают виды призм Имеют представление о площади поверхности призмы (боковой и полной), знают формулу вычисления площади поверхности призмы задач. Владеют основными видами публичных выступлений. Имеют представление о виде многогранников – пирамиде, знают определение и виды пирамиды, умеют характеризовать правильные пирамиды, знают и описывают их свойства. Умеют вступать в речевое общение, участвовать в диалоге. Имеют представление о виде многогранников – пирамиде, усеченной пирамиде, знают определение и виды пирамиды, умеют характеризовать правильные пирамиды, знают и описывают их свойства Имеют представление о правильных многогранниках, знают виды правильных многогранников. Воспроизведение изученных правил и понятий, подбор аргументов, соответствующих решению, могут работать с чертежными инструментами. Могут четко различать виды многогранников, знают характерные их свойства, умеют изображать их на чертежах и решать задачи с многогранниками. Могут работать по заданному алгоритму, аргументировать решение и найденные ошибки, участие в диалоге. Учащихся демонстрируют: систематические сведения о многогранных углах, о выпуклых многогранниках и правильных многогранники на теоретическом зачете. Учащихся демонстрируют: систематические сведения о многогранных углах, о выпуклых многогранниках и правильных многогранники на практической работе. – владеть навыками самоанализа и самоконтроля	К	СП
	г	Виды многогранников				ИР, ПП		К	ФО
	г	Призма				ИР, ПП		ПЗУ	ВП
	г	Пирамида	§2			ИР Р		ОНМ	ФО
	г	Решение задач на свойства призмы и пирамиды				ИР Р		ЗИ	ВП
	г	Усеченная пирамида				ПП		К	ФО
	г	Решение задач на свойства усеченной пирамиды				Р		ПЗУ	РК
	г	Многогранники	§3			ИР ПП		ОНМ	ФО
	г	Правильные многогранники						К	ИО
	г	Виды многогранников							ВП
	г	Свойства правильных многогранников							ПДЗ
	г	Решение задач «Правильные многогранники»				Р, ТР		ПЗУ	ВП
	г	Контрольная работа № 9 «Многогранники»	Гл. 3					ПКЗУ	КР
	г	Зачёт № 3 «Многогранники»	Гл. 3					ПКЗУ	З, ИО
Глава 5. Производная – 31 ч
	а	Числовые последовательности (определение, примеры, свойства)	§ 24		УЛ, ДМ, ДКИМ	ИР	Знать определение числовой последовательности и способы ее задания. Уметь: – определять понятия, приводить доказательства; – воспринимать устную речь, участвовать в диалоге, аргументированно рассуждать и обобщать, приводить примеры Знать и приводить примеры на свойства числовой последовательности. Уметь: – объяснить изученные положения на самостоятельно подобранных конкретных примерах; – использовать данные правила и формулы, аргументировать решение, правильно оформлять работу Знать определение предела числовой последовательности; свойства сходящихся последовательностей. Уметь: – составлять текст научного стиля; – собрать материал для сообщения по заданной теме Знать способы вычисления пределов последовательностей; как найти сумму бесконечной геометрической прогрессии. Уметь развернуто обосновывать суждения; определять понятия, приводить доказательства Знать понятие о пределе функции на бесконечности и в точке. Уметь: – посчитать приращение аргумента и функции; вычислить простейшие пределы; – собрать материал для сообщения по заданной теме Знать понятие о производной функции, геометрическом смысле производной. Уметь работать с учебником, отбирать и структурировать материал Знать понятие о производной функции, физический смысл производной. Отражение в письменной форме своих решений, рассуждение, выступление с решением проблемы Уметь: – находить производные суммы, разности, произведения, частного; производные основных элементарных функций; – собрать материал для сообщения по заданной теме Знают понятие сложной функции; могут составлять сложные функции и их дифференцировать – владеть навыками самоанализа и самоконтроля

1 2 3 4 5