|
Протокол № от августа 2015 г. Председатель педагогического совета
Муниципальное общеобразовательное учреждение
«Гимназия №44»
ПРИНЯТА
на заседании педагогического
совета МБОУ «Гимназия №44»
Протокол № ___ от __ августа 2015 г.
Председатель
педагогического совета
_____________ З.П. Богдановская
УТВЕРЖДЕНА
приказом МБОУ «Гимназия №44»
№ ____ от ____________ 2015 г.
Директор МБОУ «Гимназия №44»
_____________ З.П. Богдановская
РАБОЧАЯ ПРОГРАММА
по предмету Математика («Алгебра и начала анализа»)
СРЕДНЕЕ ОБЩЕЕ ОБРАЗОВАНИЕ
11 КЛАСС
ПРОФИЛЬНЫЙ УРОВЕНЬ
Составители: заместитель директора по УВР Шварц Т.В. ,
учитель математики Громашева Н.В.
2015г.
Пояснительная записка
Программа по алгебре и началам анализа для 11 класса составлена на основе Федерального компонента государственного образовательного стандарта общего образования, примерной образовательной программы, рекомендованной Министерством образования и науки РФ (приказ Министерства образования и науки РФ от 05.03.2004г),
Образовательная программа гимназии на 2015-2016 учебный год,
учебного плана гимназии, учебника «Алгебра и начала анализа. 11 класс», учебник профильного уровня / А. Г. Мордкович П. В. Семенов. - М.: Мнемозина, 2013, примерной авторской программы.
Задачи изучения математики на профильном уровне:
систематизация сведений о числах; изучение новых видов числовых выражений и формул; совершенствование практических навыков и вычислительной культуры, расширение и совершенствование алгебраического аппарата, сформированного в основной школе, и его применение к решению математических и нематематических задач;
изучение свойств пространственных тел, формирование умения применять полученные знания для решения практических задач;
расширение и систематизация общих сведений о функциях, пополнение класса изучаемых функций, иллюстрация широты описания и изучения реальных зависимостей;
получение представлений о вероятностно-статистических закономерностях в окружающем мире;
совершенствование интеллектуальных и речевых умений путем обогащения математического языка;
развитие логического мышления;
знакомство с основными идеями и методами математического анализа
Роль программы в образовательном маршруте обучающихся и преемственность обучения заключается в адаптации обучения математики и смежных с ней наук, в овладении математическими знаниями и умениями, необходимыми в повседневной жизни, для изучения школьных естественно – научных дисциплин на базовом уровне, для получения образования в областях, требующих углубленной математической подготовки.
Задачи программы.
Программа призвана сформировать умение самостоятельно и мотивированно организовывать свою познавательную деятельность (от постановки целей до получения и оценки результата), владеть элементарными навыками прогнозирования;
в области информационно – коммуникативной деятельности предполагается : поиск необходимой информации из источников, созданных в различных знаковых системах ( текстах, таблицах, графиках, диаграммах); ориентация в литературе по математике; передача содержания информации адекватно поставленной цели (сжато, полно, выборочно), объяснение изученных положений на самостоятельно подобранных конкретных примерах;
в области рефлексивной деятельности: объективное оценивание своих учебных достижений; навыки организации участия в коллективной деятельности; постановка общей цели и определение средств её достижений.
Формы организации учебного процесса:
индивидуальные,
групповые,
индивидуально-групповые,
фронтальные,
классные и внеклассные.
Место предмета в базисном учебном плане
Согласно Федеральному базисному учебному плану для общеобразовательных учреждений Российской Федерации для профильного изучения в 11 классе отводится на курс «Алгебра и начала анализа» 136 часов (4 часа в неделю). Из них: контрольных работ – 7; л/р - 3; тестов- 8; зачетов-3. Построен курс в форме последовательных тематических блоков с чередованием материала по алгебре, анализу, дискретной математике.
Изучение математики на про�фильном уровне направлено на достижение следующих результатов освоения:
развитие логического и критического мышления, культуры речи, способности к умственному эксперименту;
формирование у обучающихся интеллектуальной честности и объективности, способности к преодолению мыслительных стереотипов, вытекающих из обыденного опыта;
воспитание качеств личности, обеспечивающих социальную мобильность, способность принимать самостоятельные решения;
формирование качеств мышления, необходимых для адаптации в современном информационном обществе;
развитие интереса к математическому творчеству и математических способностей;
воспитание средствами математики культуры личности: знакомство с историей развития математики, эволюцией математических идей, по�нимание значимости математики для общественного прогресса.
формирование представлений о математики как части общечеловеческой культуры, о значимости математики в развитии цивилизации и современного общества;
развитие представлений о математике как форме описания и методе познания действительности, создание условий для приобретения опыта математического моделирования;
формирование общих способов интеллектуальной деятельности, характерных для математики и являющихся основой познавательной культуры, значимой для различных сфер человеческой деятельности;
формирование представлений об идеях и методах математики; о математике как уни�версальном языке науки, средстве моделирова�ния явлений и процессов;
овладение устным и письменным математическим языком, математическими знаниями и умениями, необходимыми для изучения школьных естественнонаучных дисциплин, для продолжения образования и освоения из�бранной специальности на современном уровне;
развитие логического мышления, алгорит�мической культуры, пространственного воображения, развитие математического мышления и интуиции, творческих способностей на уровне, необходимом для продолжения образования и для самостоятельной деятельности в области математики и её прило�жений в будущей профессиональной деятельности;
Третья ступень образования является завершающим этапом общеобразовательной подготовки, обеспечивающим освоение обучающимися общеобразовательных программ среднего общего образования, развитие устойчивых познавательных интересов и творческих способностей обучающихся, формирование навыков самостоятельной учебной деятельности. Она направлена на формирование компетентности школьника в различных сферах жизнедеятельности (не только в собственно познавательной или учебной) и устойчивую мотивацию к обучению.
Критерии и нормы оценки знаний,
умений и навыков учащихся.
Сущность контроля и оценки результатов обучения.
Контроль и оценка результатов освоения программы является весьма существенной составляющей процесса обучения и одной из важных задач педагогической деятельности учителя.
Система контроля и оценки позволяет установить персональную ответственность учителя и школы в целом за качество процесса обучения.
Система контроля и оценивания учебной работы обучающегося не ограничивается утилитарной целью - проверкой усвоения знаний и выработкой умений и навыков по конкретному учебному предмету. Она ставит более важную социальную задачу: развить у школьников умение проверять и контролировать себя, критически оценивать свою деятельность, устанавливать ошибки и находить пути их устранения.
При организации контроля и оценки знаний и УУД учителю необходимо учитывать следующее функциональное назначение контроля.
Социальная функция проявляется в требованиях, предъявляемых обществом к уровню подготовки обучающегося на каждом этапе обучения.
В ходе контроля проверяется соответствие достигнутых обучающимися знаний-умений-навыков (компетентностей) установленным государственным стандартом, а оценка выражает реакцию на степень и качество этого соответствия («5»-отлично, «4»-хорошо, «3»-удовлетворительно, «2»-неудовлетворительно). Т.о., в конечном счёте, система контроля и оценки для учителя является инструментом оповещения обучающихся и родителей данного образовательного учреждения. Это даёт основание для прогнозирования направлений развития образования в ближайшей и отдалённой перспективе, внесения корректировок в систему преподавания и контроля, оказания необходимой помощи как обучающемуся, так и учителю.
Образовательная функция определяет результат сравнения ожидаемого эффекта обучения с действительным.
Воспитательная функция выражается в формировании положительных мотивов учения и готовности к самоконтролю как фактору преодоления заниженной самооценки учащихся и тревожности.
Эмоциональная функция проявляется в том, что оценка деятельности обучающихся создаёт определённый эмоциональный фон и вызывает соответствующую эмоциональную реакцию.
Информационная функция является основой диагноза планирования и прогнозирования. Главная её особенность - возможность проанализировать причины неудачных результатов и наметить конкретные пути улучшения учебного процесса как со стороны ведущего этот процесс, так и со стороны ведомого.
Функция управления очень важна для развития самоконтроля школьника, его умения анализировать и правильно оценивать свою деятельность, адекватно принимать оценку педагога.
Виды контроля результатов обучения
Текущий контроль - наиболее оперативная, динамичная и гибкая проверка результатов обучения. Он сопутствует процессу становления умения и навыка, поэтому проводится на первых этапах обучения. Его основная цель - анализ хода формирования знаний , умений и УУД.
Тематический контроль заключается в проверке усвоения
программного материала и УУД по каждой крупной теме курса, а отметка фиксирует результат.
Итоговый контроль проводится как оценка результатов обучения за определённый, достаточно большой промежуток учебного времени — четверть, полугодие, год.
Методы и формы организации контроля.
Устный опрос требует связного повествования о конкретном объекте окружающего мира. Такой опрос может строиться как монологический ответ по изученному материалу и как диалог учителя с одним обучающимся или полилог со всем классом. Для учебного диалога очень важна продуманная система вопросов, которые проверяют не только способность учеников запомнить и воспроизвести информацию, но и осознанность усвоения, способность рассуждать, высказывать своё мнение, аргументированно строить ответ, активно участвовать в общей беседе, умение конкретизировать общие понятия.
Письменный опрос заключается в проведении различных самостоятельных и контрольных работ.
Самостоятельная письменная работа - небольшая, рассчитанная на урок или его часть проверка знаний, умений и УДД обучающихся. Одной из главных целей этой работы является проверка усвоения школьниками способов решения учебных задач, осознание понятий, ориентировка в конкретных правилах и закономерностях. Если самостоятельная работа проводится на начальном этапе (обучающая), то она не оценивается. Вместо неё учитель даёт аргументированный анализ работы обучающихся, который он проводит совместно с учениками. Если умение находится на стадии закрепления, автоматизации, то самостоятельная работа оценивается. Самостоятельная работа может проводиться фронтально, небольшими группами и индивидуально.
Контрольные работы используются при фронтальном текущем и итоговом контроле с целью проверки знаний и умений обучающихся по достаточно крупной и полностью изученной теме программы.
К стандартизированным методикам проверки успеваемости относятся тестовые задания. Они привлекают внимание тем, что дают точную количественную характеристику не только уровня достижений обучающегося по конкретному предмету, но также могут выявить уровень общего развития: умения применять знания в нестандартной ситуации, находить способ построения учебной задачи, сравнивать правильный и неправильный ответы и т.п. При планировании контрольных работ в каждом классе необходимо предусмотреть их равномерное распределение в течение всей четверти. Не рекомендуется проводить контрольные работы в первый день четверти, в первый день после праздника, в понедельник. В один рабочий день не рекомендуется проводить более одной письменной контрольной работы в одном классе, а в течение недели - не более двух. Время проведения итоговых контрольных работ в целях предупреждения перегрузки учащихся определяется общешкольным графиком. При оценивании необходимо учитывать не только возрастные особенности школьников, но и психологические особенности каждого обучающегося. Не менее важно требование объективности оценки.
Творческие работы. Они выполняются дома по одной из предлагаемых тем. Работы выполняются самостоятельно. Затем проводится защита творческой работы (7-10 минут) в виде доклада. Экспертная комиссия и дети, защищающие свои работы, задают вопросы докладчику. Доклад и текст работы оцениваются отдельно.
Творческие работы сдаются в письменном виде и представляют собой текст объёмом от 5 до 15 тетрадных страниц. В конце текста прилагается список использованной литературы. Работы можно выполнять в жанре эссе, научного реферата, проблемного очерка и т.д.
Критерии оценки творческих работ:
1. Умение самостоятельно работать с информацией;
2. Связанность, логичность и красота изложения;
3. Оригинальность мышления и анализ проблемы.
Контроль и оценка результатов обучения математике.
Оценка устных ответов по математике.
«5» ставится, если обучающийся полно раскрыл содержание материала в объёме, предусмотренном программой и учебником; изложил материал грамотным языком в определённой логической последовательности, точно используя математическую терминологию и символику; правильно выполнил рисунки, чертежи, графики, сопутствующие ответу; показал умение иллюстрировать теоретические положения конкретными примерами, применять их в новой ситуации при выполнении практического задания; продемонстрировал усвоение ранее изученных сопутствующих вопросов, сформированность и устойчивость используемых при ответе умений и навыков; отвечал самостоятельно, без наводящих вопросов учителя. Возможны одна-две неточности при освещении второстепенных вопросов или в выкладках, которые ученик легко исправил после замечания учителя.
«4» ставится, если ответ удовлетворяет в основном требованиям на оценку «5», но при этом имеет один из недостатков: в изложении допущены небольшие пробелы, не исказившие математическое содержание ответа, исправленные после замечания учителя; допущены 1-2 недочёта при освещении основного содержания ответа, исправленные после замечания учителя; допущены ошибка или более двух недочётов при освещении второстепенных вопросов или в выкладках, легко исправленные после замечания учителя.
«3» ставится, если обучающийся неполно или непоследовательно раскрыл содержание материала, но показал общее понимание вопроса и продемонстрировал умения, достаточные для дальнейшего усвоения программного материала (определённые «Требованиями к математической подготовке учащихся»); если у обучающегося имелись затруднения или им были допущены ошибки в определении понятий, использовании математической терминологии, чертежах, выкладках, исправленные после нескольких наводящих вопросов учителя; если обучающийся не справился с применением теории в новой ситуации при выполнении практического задания, но выполнил задания обязательного уровня сложности по данной теме; если обучающийся при знании теоретического материала показал недостаточную сформированность основных умений и навыков.
«2» ставится, если обучающийся не раскрыл основное содержание учебного материала; обнаружил незнание или непонимание большей или наиболее важной части учебного материала; допустил и не исправил даже после наводящих вопросов учителя ошибки в определении понятий, при использовании математической терминологии, в рисунках, чертежах или графиках, выкладках; если обучающийся обнаружил полное незнание и непонимание изучаемого учебного материала или не смог ответить ни на один из поставленных вопросов по изученному материалу.
Оценка письменных контрольных работ по математике.
«5» ставится, если работа выполнена полностью; в логических рассуждениях и обосновании решения нет пробелов и ошибок; в решении нет математических ошибок (возможна одна неточность, описка, которая не является следствием незнания или непонимания учебного материала).
«4» ставится, если работа выполнена полностью; но обоснование «шагов» решения недостаточно; допущена одна ошибка или 2-3 недочёта в выкладках, рисунках, чертежах или графиках.
«3» ставится, если допущено более одной ошибки или более 2-3 недочётов в выкладках, чертежах или графиках, но обучающийся обладает обязательными умениями по проверяемой теме.
«2» ставится, если в работе допущены существенные ошибки, выявившие, что обучающийся не обладает обязательными умениями по данной теме в полной мере или если работа показала полное отсутствие у обучающегося обязательных знаний и умений по проверяемой теме и значительная часть работы выполнена не самостоятельно.
Учитель может повысить оценку за оригинальный ответ на вопрос или оригинальное решение задачи, которые свидетельствуют о высоком математическом развитии обучающегося.
Основное содержание программы по математике (модуль «АЛГЕБРА И НАЧАЛА АНАЛИЗА»)
(136 часов)
Повторение(4 ч)
Повторение курса алгебры и начала анализа за курс 10 класса. Тригонометрические уравнения. Тригонометрические преобразования. Производные и их применение. Задания ЕГЭ.
Многочлены (10ч)
Многочлены от одной и нескольких переменных. Теорема Безу. Схема Горнера. Симметрические и однородные многочле�ны. Уравнения высших степеней.
Знать: определение многочлена, симметричных и однородных многочленов, теорему Безу, схему Горнера.
Уметь: применять теорему Безу и схему Горнера, решать уравнения высших степеней.
Степени и корни. Степенные функции(24 ч)
Понятие корня n-й степени из действительного числа. Функ�ции  , их свойства и графики. Свойства корня п-й степени. Преобразование выражений, содержащих радикалы. Обобщение понятия о показателе степени. Степенные функции, их свойства и графики. Извлечение корней n-й степени из комплексных чисел. , их свойства и графики. Свойства корня п-й степени. Преобразование выражений, содержащих радикалы. Обобщение понятия о показателе степени. Степенные функции, их свойства и графики. Извлечение корней n-й степени из комплексных чисел.
Знать: определение корня n-й степени из действительного числа, функ�ции  , степенной функции их свойства. , степенной функции их свойства.
Уметь: преобразовывать выражения, содержащие радикалы, строить графики степенных функций и описывать их свойства, извлекать корень из комплексного числа.
Показательная и логарифмическая функции (31ч)
Показательная функция, ее свойства и график. Показатель�ные уравнения и неравенства. Понятие логарифма. Функция 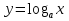 , ее свойства и график. , ее свойства и график.
Свойства логарифмов. Логарифмические уравнения и нера�венства. Дифференцирование показательной и логарифмической функций.
Знать: определение показательной и логарифмической функций, показательного и логарифмического уравнения и неравенства, свойства логарифмов, формулы для нахождения производных показательной и логарифмической функций.
Уметь: строить графики показательной и логарифмической функций и описывать их свойства, решать показательные и логарифмические уравнения и неравенства, находить производную показательной и логарифмической функций.
Интеграл (9ч)
Первообразная и неопределенный интеграл. Определенный интеграл, его вычисление и свойства. Вычисление площадей пло�ских фигур. Примеры применения интеграла в физике.
Знать: определение первообразной и интеграла, свойства интеграла.
Уметь: вычислять первообразные и интеграл, площади плоских фигур.
Элементы комбинаторики, статистики и теории вероятностей (9ч)
Вероятность и геометрия. Независимые повторения испыта�ний с двумя исходами. Статистические методы обработки инфор�мации. Гауссова кривая. Закон больших чисел.
Знать: определение вероятности, независимого испытания. статистические методы обработки информации, закон больших чисел.
Уметь: решать простейшие задачи на вероятность с использованием известных формул, вычислять вероятности событий на основе подсчёта числа исходов, выполнять статистическую обработку информации.
Уравнения и неравенства. Системы уравнений и неравенств (33ч)
Равносильность уравнений. Общие методы решения уравне�ний. Уравнения с модулями. Иррациональные уравнения. Доказа�тельство неравенств. Решение рациональных неравенств с одной переменной. Неравенства с модулями. Иррациональные неравен�ства. Уравнения и неравенства с двумя переменными. Диофантовы уравнения. Системы уравнений. Уравнения и неравенства с параметрами.
Знать: определение равносильных уравнений, неравенств, систем уравнений и неравенств, совокупности уравнений и неравенств, общие методы решения уравнений и неравенств.
Уметь: решать уравнения, неравенства, системы уравнений и неравенств, совокупности уравнений и неравенств, применять общие методы решения уравнений и неравенств.
Повторение(16 ч)
Повторение курса алгебры и начал анализа за курс 10-11 классов. Подготовка к ЕГЭ.
ТРЕБОВАНИЯ К УРОВНЮ ПОДГОТОВКИ ВЫПУСКНИКОВ
Изучения алгебры и начал анализа дает возможность обучающимся достичь следующих результатов развития:
умение ясно, точно, грамотно излагать свои мысли в устной и письменной речи, понимать смысл поставленной задачи, выстраивать аргументацию, приводить примеры и контрпримеры;
критичность мышления, умение распознавать логически некорректные высказывания, отличать гипотезу от факта;
представление о математической науке как сфере человеческой деятельности, об этапах ее развития о ее значимости для развития цивилизации;
креативность мышления, инициатива, находчивость, активность при решении математических задач;
умение контролировать процесс и результат учебной математической деятельности;
способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений;
представление об идеях и о методах математики как об универсальном языке науки и техники, о средстве моделирования явлений и процессов;
умение видеть математическую задачу в контексте проблемной ситуации в других дисциплинах, в окружающей жизни
умение находить в различных источниках информацию, необходимую для решения математических проблем, и представлять ее в понятной форме; принимать решение в условиях неполной и избыточной, точной и вероятностной информации;
умение выдвигать гипотезы при решении учебных задач и понимать необходимость их проверки;
умение применять индуктивные и дедуктивные способы рассуждений, видеть различные стратегии решения задач;
понимать сущности алгоритмических предписаний и умение действовать в соответствии с предложенным алгоритмом;
умение самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем;
умение планировать и осуществлять деятельность, направленную на решение задач исследовательского характера;
● значение практики и вопросов, возникающих в самой математике, для формирования и развития математической науки ;
● идеи расширения числовых множеств как способа построения нового математического аппарата для решения практических задач и внутренних задач математики;
значение идей, методов и результатов алгебры и математического анализа для построения моделей реальных процессов и ситуаций;
универсальный характер законов логики математических рассуждений, их применимость в различных областях человеческой деятельности;
различие требований, предъявляемых к доказательствам в математике, естественных, социально-экономических и гуманитарных науках, на практике;
роль аксиоматики в математике; возможность построения математических теорий на аксиоматической основе; значение аксиоматики для других областей знания и для практики;
вероятностный характер различных процессов и закономерностей окружающего мира.
Алгебра
Уметь:
● выполнять арифметические действия, сочетая устные и письменные приёмы, применение вычислительных устройств; пользоваться оценкой и прикидкой при практических расчетах;
● проводить по известным формулам и правилам преобразования буквенных выражений, включающих степени и тригонометрические функции;
● вычислять значения числовых и буквенных выражений, осуществляя необходимые подстановки и преобразования
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
● практических расчетов по формулам, включая формулы. содержащие степени, тригонометрические функции, используя при необходимости справочными материалами и простейшие вычислительные устройства.
Функции и графики.
Уметь:
• определять значение функции по значению аргумента при различных способах задания функции;
● строить графики изученных функций;
● описывать по графику и в простейших случаях по формуле поведение функции и свойства функции, находить по графику функции наибольшие и наименьшие значения функции;
● решать уравнения, простейшие системы уравнений, используя свойства функций и их графиков;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
• описания с помощью функций различных зависимостей, представления их графически, интерпретация графиков.
Начала математического анализа.
Уметь:
● вычислять производные элементарных функций, используя справочные материалы;
● исследовать в простейших случаях на монотонность, находить наибольшие и наименьшие значения функций, строить графики многочленов и простейших рациональных функций с использованием аппарата математического анализа;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
● решения прикладных задач , в том числе социально- экономических и физических, на наибольшие и наименьшие значения, на нахождение скорости и ускорения.
Уравнения и неравенства.
Уметь:
● решать рациональные уравнения и неравенства, простейшие тригонометрические уравнения, их схемы; решать уравнения и неравенства с модулем методом интервалов;
● составлять уравнения и неравенства по условию задачи;
● использовать для приближенного решения уравнений и неравенств графический метод;
● изображать на координатной плоскости множества решений простейших уравнений и их систем;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
● построения и исследования простейших математических моделей.
Элементы комбинаторики, статистики и теории вероятностей.
Уметь:
● решать простейшие комбинаторные задачи методом перебора, а также с использованием известных формул;
● вычислять в простейших случаях вероятности событий на основе подсчета числа исходов;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
● анализа реальных числовых данных, представленных в виде диаграмм, графиков;
● анализа информации статического характера.
Поурочно -тематическое планирование по алгебре и началам математического анализа, 11 класс
Учебник А.Г.Мордкович, П.В.Семенов (4 часа в неделю, всего 136 часов)
№ урока
|
Содержание
учебного
материала
|
Количество часов
|
Характеристика
основных видов
деятельности
учащихся
|
Формы контроля
|
1-4
|
Повторение материала 10 класса
|
4
|
Актуализировать знания по алгебре и началам анализа 10-го класса; выполнять преобразования тригонометрических выражений и решать тригонометрические уравнения разного уровня сложности; вычислять производные по таблице производных, производную суммы, произведения, частного функций; находить производную сложной функции, решать задачи на применение производной; применять полученные за 10 класс знания при выполнении теста по проверке остаточных знаний.
|
тест
(4)
|
|
Глава 1. Многочлены
|
10
|
|
|
5-7
|
§ 1. Многочлены от одной переменной
|
3
|
Выполнять арифметические операции над многочленами от одной переменной, делить многочлен на многочлен с остатком, раскладывать многочлены на множители; . применять полученные знания по данной теме при выполнении самостоятельной работы.
|
с/р
(7)
|
8-10
|
§ 2. Многочлены от нескольких переменных
|
3
|
Различать однородные, симметрические многочлены от нескольких переменных и их системы, знать способы их решения. Решать различными способами задания с однородными и симметрическими многочле-нами от нескольких переменных; применять полученные знания по данной теме при выполнении самостоятельной работы.
|
с/р
(10)
|
11-12
|
§ 3. Уравнения высших степеней
|
2
|
Знать методы решения уравнений высших степеней: метод разложения на множители и метод введения новой переменной. Знать функционально-графический метод решения уравнений высших степеней.
|
|
13
|
Контрольная работа № 1
по теме "Многочлены"
|
1
|
Демонстрировать знания о многочленах от одной и нескольких переменных, о методах решения уравнений высших степеней. Владеть навыками самоанализа и самоконтроля; свободно пользоваться знаниями о многочленах от одной и нескольких переменных, о методах решения уравнений высших степеней.
|
к/р
|
14
|
Резерв
|
1
|
|
|
|
Глава 2. Степени и корни. Степенные функции.
|
24
|
|
|
15-16
|
§ 4. Понятие корня n-ой степени из действительного числа
|
2
|
Знать определение корня
n-ой степени, его свойства; выполнять преобразования выражений, содержащих радикалы, содержащие корни n-ой степени ; вступать в речевое общение; самостоятельно искать и отбирать необходимую для решения учебных задач информацию.
|
|
17-19
|
§ 5. Функции y=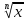 , их свойства и графики , их свойства и графики
|
3
|
Определять значение функции по значению аргумента при различных способах задания функции; строить график функции; использовать для решения познавательных задач справочную литературу; применять свойства функций; исследовать функцию по схеме, при построении графиков использовать правила преобразования графиков; объяснять изученные положения на самостоятельно подобранных конкретных примерах; обосновывать суждения, давать определения, приводить доказательства, примеры.
|
|
20-22
|
§ 6. Свойства корня n-ой степени
|
3
|
Знать свойства корня n-й степени, уметь преобразовывать выражения, содержащие радикалы; применять свойства корня
n-й степени, уметь на творческом уровне пользоваться ими при решении задач; находить и использовать информацию; применять полученные знания по данной теме при выполнении тестовых заданий.
|
тест
(22)
|
23-26
|
§ 7. Преобразование выражений, содержащих радикалы
|
4
|
Выполнять арифметические действия, сочетая устные и письменные приемы; находить значения корня натуральной степени, по известным формулам и правилам преобразования буквенных выражений, включающих радикалы; применять полученные знания по данной теме при выполнении самостоятельной работы.
|
с/р
(25)
|
27-28
|
Контрольная работа № 2 по теме " Степени и корни. Степенные функции".
|
2
|
Демонстрировать знания о корне n – й степени из действительного числа и его свойствах, о функции  , ее свойствах и графиках, о преобразованиях выражений, содержащих радикалы при выполнении контрольной работы. , ее свойствах и графиках, о преобразованиях выражений, содержащих радикалы при выполнении контрольной работы.
|
к/р
|
29-31
|
§ 8. Понятие степени с любым рациональным показателем
|
3
|
Находить значения степени с рациональным показателем; проводить по известным формулам и правилам преобразования буквенных выражений, обобщать понятие о показателе степени, выполняя преобразование выражений, содержащих радикалы; обосновывать суждения, давать определения, приводить доказательства, примеры включающих степени; применять полученные знания по данной теме при выполнении тестовых заданий .
|
тест
(31)
|
32-35
|
§ 9. Степенные функции, их свойства и графики
|
4
|
Строить графики степенных функций при различных значениях показателя; описывать по графику и в простейших случаях по формуле поведение и свойства функций, находить по графику функции наибольшие и наименьшие значения; демонстрировать теоретические и практические знания по теме "Степени и корни. Степенная функция" в ходе выполнения зачёта.
|
зачёт
(35)
|
36-37
|
§ 10. Извлечение корня из комплексного числа
|
2
|
Выполнять арифметические действия над комплексными числами в разных формах записи; знать комплексно сопряженные числа, извле-кать корень из комплексного числа; приводить примеры, подбирать аргументы, формулировать выводы; составлять текст научного стиля; применять полученные знания по данной теме при выполнении самостоятельной работы.
|
с/р
(37)
|
38
|
Контрольная работа № 3 по теме " Степени и корни. Степенные функции".
|
1
|
Демонстрировать теорети-ческие и практические знания по теме «Степени и корни. Степенная функция» в ходе выполнения контрольной работы.
|
к/р
|
|
Глава 3. Показательная и логарифмическая функции
|
31
|
|
|
39-41
|
§ 11. Показательная функция, её свойства и график
|
3
|
Распознавать показательную функцию; формулировать ее свойства, строить схематический график любой показательной функции; проводить описание свойств показательной функции по заданной формуле, применяя возможные преобразования графиков; работать с учебником, отбирать и структурировать материал; самостоятельно проводить построение и исследование графика показательной функции в ходе выполнения лабораторной работы.
|
лаб/раб.
( 41 )
|
42-44
|
§ 12. Показательные уравнения
|
3
|
Распознавать показательные уравнения; решать простейшие показательные уравнения, их системы; использовать для приближенного решения уравнений графический метод; решать показательные уравнения, применяя комбинацию нескольких алгоритмов; изображать на координатной плоскости множества решений простейших уравнений, и их систем.
|
|
45-46
|
§ 13. Показательные неравенства
|
2
|
Распознавать показательные неравенства; решать простейшие показательные неравенства, их системы; использовать для приближенного решения неравенств графический метод; решать показательные неравенства, применяя комбинацию нескольких алгоритмов; изображать на координатной плоскости множества решений простейших неравенств и их систем; применять полученные знания по данной теме при выполнении тестовых заданий .
|
тест
(46)
|
47-48
|
Контрольная работа № 4-
промежуточный контроль знаний за I полугодие в формате ЕГЭ.
|
2
|
Применять полученные знания по алгебре и началам анализа за I полугодие в промежуточном контроле в виде теста в формате ЕГЭ.
|
тест в формате ЕГЭ
|
49-51
|
§ 14. Понятие логарифма
|
2
|
Устанавливать связь между степенью и логарифмом; понимать их взаимно противоположное значение; вычислять логарифм числа по определению; передавать информацию сжато, полно, выборочно; выполнять преобразования логарифми-ческих выражений; вычислять логарифмы чисел.
|
|
52-53
|
§ 15. Логарифмическая функция, её свойства и график
|
3
|
Распознавать логарифмическую функцию; строить график функции; определять значение функции по значению аргумента при различных способах задания функции; формулировать её свойства в зависимости от основания; строить схематический график любой логарифмической функции; на творческом уровне исследовать функцию по схеме; владеть приёмами построения и исследования математи-ческих моделей ; само-стоятельно проводить построение и исследование графика логарифмической функции в ходе выполнения лабораторной работы.
|
лаб/раб.
( 53 )
|
54-57
|
§ 16. Свойства логарифмов
|
4
|
Находить значения логарифма; выполнять арифметические действия, сочетая устные и письменные приёмы; проводить по известным формулам и правилам преобразования буквенных выражений, включающих логарифмы ; знать формулу перехода к новому основанию и два частных случая формулы перехода к новому основанию логарифма ; применять свойства логарифмов ; применять формулу основанию и два частных случая формулы перехода к новому основанию логарифма; на творческом уровне проводить по известным формулам и правилам преобразования буквенных выражений, включающих логарифмы ; обосновывать суждения, давать определения, приводить доказательства, примеры; применять полученные знания по данной теме при выполнении тестовой работы.
|
тест
(56)
|
58-61
|
§ 17. Логарифмические уравнения
|
4
|
Иметь представления о логарифмических уравнениях; определять понятия, приводить доказательства; решать простейшие логарифмические уравнения по определению, с помощью метода введения новой переменной; решать простейшие системы логарифмических уравнений; использовать для приближённого решения уравнений графический метод; изображать на координатной плоскости множества решений простейших логарифмических уравнений и их систем; применять полученные знания по данной теме при выполнении самостоятельной работы.
|
с/р
(61)
|
62-64
|
§ 18. Логарифмические неравенства
|
3
|
Применять алгоритм решения логарифмических неравенств в зависимости от основания при решении логарифмических неравенств; решать простейшие логарифмические неравенства, применяя метод замены переменных для сведения логарифмического неравенства к рациональному виду; применять полученные знания по решению логарифмических уравнений и их систем; решать простейшие логарифми-ческие неравенства устно, применять свойства монотонности логариф-мической функции при решении более сложных неравенств; использовать для приближенного решения неравенств графический метод; применять полученные знания по данной теме при выполнении самостоятельной работы.
|
с/р
(64)
|
65-66
|
§ 19. Дифференцирование показательной и логарифмической функций
|
2
|
Знать формулы для нахождения производной и первообразной показа-тельной и логарифмической функций; вычислять производные и перво-образные простейших показательных и логариф-мических функций; решать практические задачи с помощью аппарата дифференциального и интегрального исчисления; демонстрировать теорети-ческие и практические знания по теме «Показательная и логариф-мическая функции»» в ходе выполнения зачётной работы.
|
зачёт
(66)
|
67-68
|
Контрольная работа № 5 по теме " Показательная и логарифмическая функции"
|
2
|
Применять полученные знания по теме "Показа-тельная и логарифмическая функции" в ходе выполнения контрольной работы.
|
к/р
|
69
|
Резерв
|
1
|
|
|
|
Глава 4. Первообразная и интеграл
|
9
|
|
|
70-72
|
§ 20. Первообразная и неопределённый интеграл
|
3
|
Иметь представление о понятии первообразной и неопределённого интеграла; находить первообразные для суммы и произведения функции на число, используя справочные материалы; вычислять неопределённые интегралы; применять свойства неопределенных интегралов в сложных творческих задачах; применять полученные знания по данной теме при выполнении самостоятельной работы.
|
с/р
(72)
|
73-77
|
§ 21. Определённый интеграл
|
5
|
Распознавать определённый интеграл и отличать его от неопределённого; применять формулу Ньютона - Лейбница для вычисления площади криволинейной трапеции в простейших задачах; вычислять площадь криволинейной трапеции с помощью первообразной.
|
|
78
|
Контрольная работа № 6 по теме " Первообразная и интеграл"
|
1
|
Демонстрировать знания о первообразной и опреде-
ленном и неопределенном интеграле, показывать умения решения прикладных задач; свободно пользоваться знаниями о первообразной и определенном и неопределенном интеграле при решении различных творческих задач в ходе выполнения контрольной работы.
|
к/р
|
|
Глава 5. Элементы теории вероятностей и математической статистики
|
9
|
|
|
79-80
|
§ 22. Вероятность и геометрия
|
2
|
Знать классическую вероятностную схему для равновозможных испыта-ний; знать правило геометрических вероят-ностей; использовать компьютерные технологии для создания базы данных; по условию текстовой задачи на нахождение вероятности строить геометрическую модель и переходить к корректно поставленной математической задаче; составлять текст научного стиля.
|
|
81-82
|
§ 23. Независимые повторения испытаний с двумя исходами
|
2
|
Решать вероятностные задачи, используя вероятностную схему Бер-нулли, теорему Бернулли, понятие многогранника распределения; добывать информацию по заданной теме в источниках различ-ного типа; приводить примеры, подбирать аргументы, формулировать выводы; применять полученные знания по данной теме при выполнении самостоятельной работы.
|
с/р
( 82)
|
83-84
|
§ 24. Статистические методы обработки информации
|
2
|
Знать понятия: общий ряд данных, выборка, варианта, кратность варианты, таблица распределения, частота варианты, график распределения частот, способы представления информации; находить частоту события, используя собственные наблюдения и готовые статистические данные; понимать статистические утверждения, встречающиеся в повседневной жизни ; использовать компьютерные технологии для создания базы данных; самостоятельно применять статистические методы обработки информации в ходе выполнения лабораторной работы.
|
лаб/раб.
( 84 )
|
85-86
|
§ 25. Гауссова кривая. Закон больших чисел
|
2
|
Решать вероятностные задачи, используя знания о гауссовой кривой, алгоритм использования кривой нормального распределения и функции площади гауссовой кривой в приближенных вычислениях, закон больших чисел; применять полученные знания по данной теме при выполнении тестовой работы.
|
тест
(86)
|
87
|
Резерв
|
1
|
|
|
|
Глава 6. Уравнения и неравенства. Системы уравнений и неравенств
|
33
|
|
|
88-91
|
§ 26. Равносильность уравнений
|
4
|
Иметь представление о равносильности уравнений; применять основные теоре-мы равносильности при решении уравнений; производить равносильные переходы с целью упрощения уравнения; иметь представление о возможных потерях или приобретениях корней и путях исправления данных ошибок; выполнять проверку найденного решения с помощью подстановки и учёта области допустимых значений.
|
|
92-94
|
§ 27. Равносильность систем уравнений
|
3
|
Применять основные методы решения алгебраических уравнений: метод разложения на множители и метод введения новой переменной при решении уравнений степени выше 2; решать простые тригонометрические, показа-тельные, логарифмические, иррациональные уравнения стандартными методами; обосновывать суждения; приводить доказательства, примеры; при решении уравнений высших степеней знать способ нахождения корней среди делителей свободного члена, иметь представление о схеме Горнера , применять ее для деления многочлена на двучлен; применять полученные знания при выполнении самосто-ятельной работы.
|
с/р
( 94)
|
95-97
|
§ 28. Равносильность неравенств
|
3
|
Решать неравенства с одной переменной; изображать на плоскости множество решений неравенства с одной переменной; приводить примеры; подбирать аргументы; формулировать выводы; знать основные способы равносильных переходов; выполнять проверку найденного решения с помощью подстановки и учета области допустимых значений; доказывать равносильность неравенств на основе теорем равносильности; предвидеть возможную потерю или приобретение корня и находить пути возможного избегания ошибок; применять полученные знания при выполнении самостоятельной работы.
|
с/р
( 97)
|
98-100
|
§ 29. Уравнения и неравенства с модулями
|
3
|
Решать уравнения и неравенства с модулем, раскрывая модуль по определению, графически и используя свойства функций входящих в выражение; находить и использовать информацию; использовать различные приемы решения уравнений и неравенств с модулем.
|
|
101-102
|
Контрольная работа № 7 по теме " Уравнения и неравенства. Системы уравнений и неравенств"
|
2
|
Применять полученные знания по теме " Уравнения и неравенства. Системы уравнений и неравенств" в ходе выполнения контрольной работы.
|
к/р
|
103-105
|
§ 30. Уравнения и неравенства со знаком радикала
|
3
|
Знать основной метод решения иррациональных уравнений и неравенств – метод возведения обеих частей уравнения в одну и туже степень, а также некоторые специфические приемы; использовать метод возведения обеих частей уравнения в одну и туже степень, а также некоторые специфические приемы при решении уравнений со знаком радикала.
|
|
106-107
|
§ 31. Доказательство неравенств
|
2
|
Использовать для доказательства неравенства методы: с помощью определения, от противного, метода математической индукции, функционально – графического метода, а также синтетический метод; применять полученные знания при выполнении самостоятельной работы.
|
с/р
( 107)
|
108-109
|
§ 32. Уравнения и неравенства с двумя переменными
|
2
|
Решать диофантово уравнение и неравенства с двумя переменными; изображать на плоскости множество решений неравенства с двумя переменными; приводить примеры; подбирать аргументы; формулировать выводы; применять полученные знания по данной теме при выполнении самостоятельной работы.
|
с/р
( 109)
|
110-113
|
§ 33. Системы уравнений
|
4
|
Иметь представление о графическом решении системы из двух или более уравнений; добывать информацию по заданной теме в источниках различного типа; графически и аналитически решать системы из двух и более уравнений; применять полученные теоретические знания по данной теме при выполнении зачётной работы.
|
зачёт
(113)
|
114-115
|
Контрольная работа № 8 по теме " Уравнения и неравенства. Системы уравнений и неравенств"
|
2
|
Применять полученные знания по теме " Уравнения и неравенства. Системы уравнений и неравенств" при выполнении контрольной работы.
|
к/р
|
116-119
|
§ 34. Задачи с параметрами
|
4
|
Решать простейшие уравне-ния и неравенства с парамет-рами; обосновывать суждения, давать определения, приводить доказательства, примеры; использовать для решения познавательных задач справочную литературу; находить и использовать информацию.
|
|
120
|
Резерв
|
1
|
|
|
121-136
|
Повторение.
|
16
|
|
|
121-124
|
Повторение по теме «Тригонометрия»
|
|
Использовать формулы и свойства тригонометрических функций; видеть применение знаний в практических ситуациях; выступать с решениями проблем; строить графики тригонометрических функций. Преобразовывать простые тригонометрические выражения; решать тригонометрические уравнения разными способами; обобщать и систематизировать знания по данной теме при выполнения тестовых заданий.
|
|
125-128
|
Повторение по теме «Графики» (задания в ЕГЭ)
|
|
Повторить, обобщить и систематизировать знания учащихся по теме "Графики" и применить приобретённые знания учащимися по данной теме к выполнению тестовой части ЕГЭ.
|
|
129-131
|
Задачи реальной математики в ЕГЭ
|
|
Повторить, обобщить и систематизировать знания по заданиям реальной математики из ЕГЭ; применять их при решении заданий ЕГЭ.
|
|
132-134
|
Промежуточный контроль знаний за год - итоговый тест в формате ЕГЭ
|
2
|
Обобщать и систематизировать знания по основным темам курса математики за 11 класс
|
тест в формате ЕГЭ
|
135-136
|
Задания по теме «Нестандартные задания в ЕГЭ и способы их решения»
|
|
Решать уравнения и их системы; неравенства и их системы нестандартными методами: с использованием областей существования функций, с использованием неотрицательности функций,
с использованием ограниченности функций, свойств синуса и косинуса, производной, числовых неравенств.
|
|
|
Всего
|
136
|
|
|
Примечание: резервное время в количестве 4 часов можно использовать на тренировочные работы , проводимые МИОО для подготовки к ЕГЭ.
Сводная таблица
|
|
|
 Скачать 425.44 Kb.
Скачать 425.44 Kb. , их свойства и графики. Свойства корня п-й степени. Преобразование выражений, содержащих радикалы. Обобщение понятия о показателе степени. Степенные функции, их свойства и графики. Извлечение корней n-й степени из комплексных чисел.
, их свойства и графики. Свойства корня п-й степени. Преобразование выражений, содержащих радикалы. Обобщение понятия о показателе степени. Степенные функции, их свойства и графики. Извлечение корней n-й степени из комплексных чисел. , степенной функции их свойства.
, степенной функции их свойства.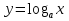 , ее свойства и график.
, ее свойства и график.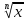 , их свойства и графики
, их свойства и графики , ее свойствах и графиках, о преобразованиях выражений, содержащих радикалы при выполнении контрольной работы.
, ее свойствах и графиках, о преобразованиях выражений, содержащих радикалы при выполнении контрольной работы.