Урок по теме «Основные понятия. Графический способ решения систем уравнений»
 Скачать 63 Kb. Скачать 63 Kb.
|
| Муниципальное общеобразовательное учреждение лицей городской округ Орехово-Зуево Урок по теме «Основные понятия. Графический способ решения систем уравнений» 9 класс Автор: Яковлева Наталья Владимировна учитель математики МОУ лицей 22.10.2012 г. Девиз: «Три пути ведут к знанию: путь размышления – это путь самый благородный, путь подражания – это путь самый легкий и путь опыта – это путь самый горький». Конфуций. Основные понятия. Графический способ решения системы уравнений с двумя переменными. Цель урока: Образовательные: расширить знания о системах уравнений с двумя переменными и на основе приобретенных знаний сформировать умение решать их графическим способом. Развивающие: развивать у учащихся мыслительную деятельность, а именно наблюдение, анализ, классификация, обобщение. Воспитательные: формировать учебную деятельность (мотивацию, понимание цели, учебных действий, действий контроля и оценки). Средства обучения: компьютер, проектор, Задачи урока:
Оборудование: проектор, экран, доска, карточки с заданием тестов, индивидуальные оценочные листы, бланки ответов. Ход урока I этап. Орг. Момент. Здравствуйте, ребята! Садитесь. Актуализация знаний. Урок у нас сегодня необычный. Все мы знакомы с курса алгебры с системами уравнений с двумя неизвестными. Давайте вспомним: некоторые важные моменты темы. - Какое уравнение называют рациональным уравнением с 2 переменными?. - Что называют решением уравнения с 2 переменными? - Какие уравнения называют равносильными? - Какие равносильные преобразования можно делать при решении уравнений? - Какие неравносильные преобразования вы знаете? - Что такое график уравнения с 2 переменными? - Установите соответствие.   окружность окружность  кубическая парабола кубическая парабола гипербола гипербола . Постановка цели урока. Раз мы знаем виды графиков уравнений с 2 переменными, то наверняка сможем решить систему уранений графическим способом..) Значит цель нашего урока какая? (ответы учащихся) (слайд) Мы с вами определили цель урока и каждый перед собой ставит свои задачи нашего урока. Решим № 5. 19 в. Решить графически систему уравнений. Ученик у доски решает. { у = -8 / х х = 2 – у. Давайте сделаем из рассмотренного примера выводы (слайд). Далее прочитать в учебнике стр 61 определение 4. Перед вами листки оценивания вашей работы на уроке. После каждого задания нужно проставить баллы, которые вы наберете в различных заданиях. Задание 1 (слайд 6) Тест 1 вариант. 1 вопрос. Какая точка находится во второй четверти координатной плоскости? 1) А(3; 7); 2) В(-5; 4); 3) С(-3; -6); 4) Д(1; -6). 2 вопрос. Решением какого уравнения является пара чисел (1;0) а) х2+у = 1; б) ху+3 = х; в) у(х+2) = 0. 1) а 2) б 3) в 3 вопрос. Окружность изображенная на рисунке задана уравнением х2 + у2 = 16. 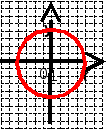  Используя этот рисунок, определите, какая из систем уравнений не имеет решения? 1) { х2 + у2 = 16 2) {х2 + у2 = 16 3) {х2 + у2 = 16 4){ х2 + у2 = 16 у= -4 у = х + 7 у = 3 – 2х у = 3х 4 вопрос. Укажите координаты центра окружности и радиус: х2+(у-5)2=9 . 1) (0; -5) 2) ( 5; 0) 3) (0; 5) 4) (0; -5) 5 вопрос. Сколько решений имеет система уравнений, изображенная на графике:  1) одно; 2)два; 3) три; 4) нет решений. 6 вопрос. Выберите правильное соответствие уравнений и графиков уравнений 1) ху = 4 а) Гипербола (1 и 3 четверти); 2) у = х -3 б) Окружность; 3) х 2 + у2 =9 в) Прямая; 4) у = - 8/х г) Парабола (ветви направлены вверх); 5) у = х2 + 2 д) Гипербола (2 и 4 четверти); е) Парабола (ветви направлены вниз); 2 вариант. 1. Какая точка находится в третьей четверти координатной плоскости? 1) А(-13; 4); 2) В(7; 4); 3) С(-2; -6); 4) Д(5; -6). 2 вопрос. Решением какого уравнения является пара чисел (0; 1) а) х+у 1) а 2) б 3) в . 3 вопрос. Окружность изображенная на рисунке задана уравнением х2 + у2 = 25 Используя этот рисунок, определите, какая из систем уравнений не имеет решения? 1    ) )  х2 + у2 = 25 2) х2 + у2 = 25 3) х2 + у2 = 25 4) х2 + у2 = 25 х2 + у2 = 25 2) х2 + у2 = 25 3) х2 + у2 = 25 4) х2 + у2 = 25у = -4 у = х + 4 у = 3 – 2х у = 6 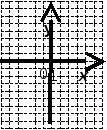  4 вопрос. Укажите координаты центра окружности и радиус: (х+2)2+у2=4 . 1) (0; 2) 2) ( 2; 0) 3) (-2; 0) 4) (0; 4) 5 вопрос. Сколько решений имеет система уравнений, изображенная на графике   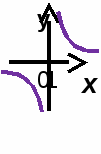 1) одно; 2)два; 3) три; 4) нет решений Установить соответствие 1) ху = -1 а) Гипербола (1 и 3 четверти); 2) у = х -3 б) Окружность; 3) х 2 + у2 = 5 в) Прямая; 4) у = х2 -4 г) Парабола (ветви направлены вверх); 5) у = 6 /х д) Гипербола (2 и 4 четверти); е) Парабола (ветви направлены вниз); А теперь проверьте свои ответы , обменявшись тетрадями.(слайд) Каждый номер оценивается в 1 балл. Сколько баллов набрали, занесите в оценочный лист. Что надо сделать, чтобы решить систему двух уравнений с двумя неизвестными? Ребята делают выводы.
Помните о двух вещах! 1. Если точек пересечения графиков нет, то система решений не имеет; 2. Координаты точек пересечения определяются приблизительно, поэтому и решения могут получиться приблизительными; Чтобы проверить точность полученных решений, их нужно подставить в уравнения системы! А теперь разгадаем кроссворд (слайд) Каждый записывает отгаданные слова в тетрадь. За каждое слово 1 балл. Если остается время решить систему графическим способом самостоятельно 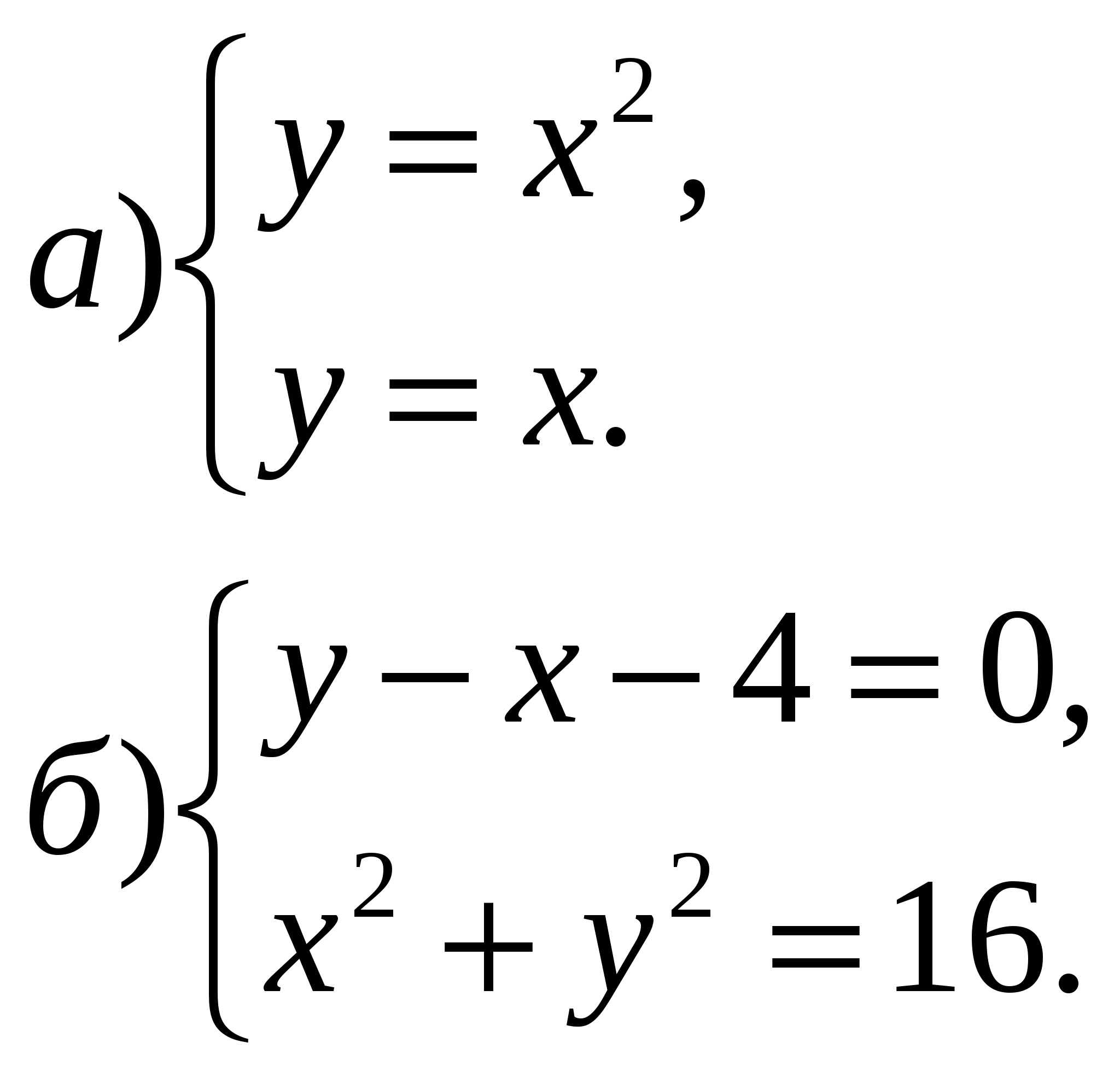   А) у = х А) у = ху = 1 Б) ху = 4 у – 2х = 2 Рефлексия (слайд) Продолжи предложение
В конце урока выставляются оценки по результатам оценочного листа. Д. З. п. 5, № 5.19г, 5.20 а. 5. 21 а |