|
Рабочая программа учителя
Антохиной Е.А.
по математике, 11 класс
«Согласовано»
Руководитель МО________
/______________ /
протокол №____ от
«___» _________ 20__г.
Рассмотрено на заседании педагогического совета
протокол № ___________ от
«____» __________ 20 __г
2014 - 2015 учебный год
Пояснительная записка
Рабочая программа по математике ориентирована на учащихся 11 класса (профильный уровень) и реализуется на основе следующих документов:
Согласно базисному учебному плану МБОУ «Глинищевская СОШ» и в продолжение начатой в средней школе линии, выбрана данная учебная программа и учебно-методический комплект.
Федеральный компонент государственного образовательного стандарта начального общего, основного общего и среднего (полного) общего образования (Приказ МО РФ от 05.03.2004 №1089).
Примерная программа основного общего образования по математике.
Федеральный базисный учебный план для среднего (полного) общего образования (Приложение к приказу Минобразования России от 09.03.2004 № 1312).
Преподавание математики в 2009/2010 учебном году. Методическое письмо/под ред. И.В. Ященко, А.В. Семёнова – М.:МИОО, 2009.-304с.
Программы для общеобразовательных школ: Математика, 5 – 6 кл. Алгебра, 7-9 кл. Алгебра и начала математического анализа, 10-11 кл. / авт.-сост. И.И. Зубарева, А.Г. Мордкович. – 2-е изд., испр. и доп. – М.: Мнемозина, 2009. – 63 с.
Программы для общеобразовательных учреждений. Геометрия, 10 – 11 кл. / Сост. Т.А. Бурмистрова / М.: Просвещение, 2009.
Общая характеристика учебного предмета
Алгебра как содержательный компонент математического образования в основной школе нацелена на формирование математического аппарата для решения задач из математики, смежных предметов, окружающей реальности. Язык алгебры подчеркивает значение математики как языка для построения математических моделей, процессов и явлений реального мира. Одной из основных задач изучения алгебры является развитие алгоритмического мышления, необходимого, в частности, для усвоения курса информатики; овладение навыками дедуктивных рассуждений. Преобразование символических форм вносит свой специфический вклад в развитие воображения, способностей к математическому творчеству. Другой важной задачей изучения алгебры является получение школьниками конкретных знаний о функциях как важнейшей математической модели для описания и исследования разнообразных процессов (равномерных, равноускоренных, экспоненциальных, периодических и др.), для формирования у учащихся представлений о роли математики в развитии цивилизации и культуры.
Геометрия – один из важнейших компонентов математического образования, необходимый для приобретения конкретных знаний о пространстве и практически значимых умений, формирования языка описания объектов окружающего мира, для развития пространственного воображения и интуиции, математической культуры, для эстетического воспитания учащихся. Изучения геометрии вносит вклад в развитие логического мышления, в формирование понятия доказательства.
В ходе освоения содержания курса учащиеся получают возможность:
развить представления о числе и роли вычислений в человеческой практике; сформировать практические навыки выполнения устных, письменных, инструментальных вычислений, развить вычислительную культуру;
овладеть символическим языком алгебры, выработать формально-оперативные алгебраические умения и научиться применять их к решению математических и нематематических задач;
изучить свойства и графики элементарных функций, научиться использовать функционально-графические представления для описания и анализа реальных зависимостей;
получить представления о статистических закономерностях в реальном мире и о различных способах их изучения, об особенностях выводов и прогнозов, носящих вероятностный характер;
развить логическое мышление и речь – умения логически обосновывать суждения, проводить несложные систематизации, приводить примеры и контрпримеры, использовать различные языки математики (словесный, символический, графический) для иллюстрации, интерпретации, аргументации и доказательства;
сформировать представления об изучаемых понятиях и методах как важнейших средствах математического моделирования реальных процессов и явлений.
Изучение математики направлено на достижение следующих целей:
овладение системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования;
интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе: ясность и точность мысли, критичность мышления, интуиция, логическое мышление, элементы алгоритмической культуры, пространственных представлений, способность к преодолению трудностей;
формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов;
воспитание культуры личности, отношения к математике как к части общечеловеческой культуры, понимание значимости математики для научно-технического прогресса.
Место предмета в федеральном базисном учебном плане
Согласно действующему в школе учебному плану в 11 классе (профильный уровень), предполагается обучение в объеме 204 часа.
Составленное календарно-тематическое планирование соответствует содержанию примерных программ основного общего образования по математике, направлено на достижение целей изучения математики и обеспечивает выполнение требований государственного стандарта математического образования.
Настоящее тематическое планирование ориентировано на действующие в настоящее время учебники математики: Л.С. Атанасян «Геометрия, 10-11»; Алгебра и начала математического анализа (профильный уровень). 11 класс. В 2 ч. Ч.1. Учебник для общеобразовательных учреждений /А.Г. Мордкович. стер. – М.: Мнемозина, 2013. – 424 с; Алгебра и начала математического анализа (профильный уровень). 11 класс. В 2 ч. Ч.2. Задачник для общеобразовательных учреждений /А.Г. Мордкович. стер. – М.: Мнемозина, 2013. –265 с.
Общеучебные умения, навыки и способы деятельности:
В ходе изучения математики в профильном курсе старшей школы учащиеся продолжают овладение разнообразными способами деятельности, приобретают и совершенствуют опыт:
проведения доказательных рассуждений, логического обоснования выводов, использования различных языков математики для иллюстрации, интерпретации, аргументации и доказательства;
решения широкого класса задач из различных разделов курса, поисковой и творческой деятельности при решении задач повышенной сложности и нетиповых задач:
планирования и осуществления алгоритмической деятельности: выполнения и самостоятельного составления алгоритмических предписаний и инструкций на математическом материале; использования и самостоятельного составления формул на основе обобщения частных случаев и результатов эксперимента; выполнения расчетов практического характера;
построения и исследования математических моделей для описания и решения прикладных задач, задач из смежных дисциплин и реальной жизни; проверки и оценки результатов своей работы, соотнесения их с поставленной задачей, с личным жизненным опытом;
самостоятельной работы с источниками информации, анализа, обобщения и систематизации полученной информации, интегрирования ее в личный опыт.
Результаты обучения
Результаты обучения задают систему итоговых результатов обучения, которых должны достигать все учащиеся, оканчивающие основную школу, и достижение которых является обязательным условием положительной аттестации ученика за курс основной школы. Эти требования структурированы по трем компонентам: «знать/понимать», «уметь», «использовать приобретенные знания и умения в практической деятельности и повседневной жизни». При этом последние два компонента представлены отдельно по каждому из разделов содержания.
Календарно – тематическое планирование
по математике
Класс ____11_____
У читель Антохина Е. А. читель Антохина Е. А.
Количество часов
Всего 204 час (136а+68г); в неделю 6 час (4а+2г).
Плановых контрольных уроков 14 (9а+5г)
Зачетов: 4 (геометрия)
Планирование составлено на основе программы для общеобразовательных учреждений. Геометрия, 10 – 11 кл. /авт.- сост. Т.А. Бурмистрова, М.: Просвещение, 2009.
Программы. Математика. 5-6 классы. Алгебра. 7-9 классы. Алгебра и начала математического анализа. 10-11 классы / авт.-сост. И.И. Зубарева, А.Г. Мордкович.– 2-е изд., испр. и доп. – М.: Мнемозина, 2009. – 63с.
Учебники: 1. Алгебра и начала математического анализа (профильный уровень). 11 класс. В 2 ч. Ч.1. Учебник для общеобразовательных учреждений /А.Г. Мордкович. стер. – М.: Мнемозина, 2013. – 424 с.
2. Алгебра и начала математического анализа (профильный уровень). 11 класс. В 2 ч. Ч.2. Задачник для общеобразовательных учреждений /А.Г. Мордкович. стер. – М.: Мнемозина, 2013. – 265 с.
3. Геометрия 10-11. Учебник для общеобразовательных учреждений / Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др. –
14-е изд. – М.: Просвещение, 2012. – 206 с.
Дополнительная литература:
В.И. Глизбург. Под ред. А.Г. Мордковича. Алгебра и начала математического анализа. Контрольные работы для учащихся общеобразовательных учреждений, 11 класс (профильный уровень). – М.: Мнемозина, 2008 г. – 62 с.
А.Г. Мордкович, П.В. Семенов. Алгебра и начала анализа. Методическое пособие для учителя. – М.: Мнемозина, 2008 г.
Дидактические материалы по геометрии для 11 класса. / Б.Г. Зив. / М. Просвещение, 2003.
Задачи по геометрии для 7 – 11 классов. , Б.Г. Зив, В.М. Мейлер, А.П. Баханский. / М.: Просвещение, 2003.
Изучение геометрии в 10 – 11 классах: Методические рекомендации к учебнику. Книга для учителя. / С.М. Саакян, В.Ф. Бутузов. / М.: Просвещение, 2001.
№
п/п
|
Дата
|
Наименование раздела, темы
|
Содержание материала
|
Коли-
чество
часов
|
Вид контроля
|
Примечание
|
|
|
АЛГЕБРА
|
ГЕОМЕТРИЯ
|
|
|
|
|
|
план
|
факт
|
Повторение материала курса алгебры 10 класса
|
|
|
5
|
|
|
|
Глава IV. Векторы в пространстве
|
|
6
|
|
1
|
|
|
Повторение. Тригонометрические уравнения
|
|
Тригонометрические уравнения; виды тригонометрических уравнений; решение простейших тригонометрических уравнений; основные тригонометрические тождества; формулы тригонометрии
|
1
|
Фронтальный опрос, индивидуальный контроль
|
|
2
|
|
|
|
Понятие вектора в пространстве
|
|
1
|
Фронтальный опрос. Самостоятельная теоретическая работа
|
|
3
|
|
|
Повторение. Решение простейших тригонометрических уравнений
|
|
Тригонометрические уравнения; виды тригонометрических уравнений; решение простейших тригонометрических уравнений; основные тригонометрические тождества; формулы тригонометрии
|
1
|
Фронтальный опрос. Взаимопроверка в группах
|
|
4
|
|
|
Повторение. Решение простейших тригонометрических уравнений
|
1
|
Фронтальный опрос, индивидуальный контроль
|
|
5
|
|
|
Повторение. Применение производной к решению задач
|
Производная, таблица производных, производная суммы, произведения, частного функций; производная сложной функции, задачи на применение производной.
|
1
|
Фронтальный опрос, индивидуальный контроль
|
|
6
|
|
|
|
Сложение и вычитание векторов
|
|
1
|
Фронтальный опрос. Самостоятельная теоретическая работа
|
|
7
|
|
|
Повторение. Применение производной к решению задач
|
|
Производная, таблица производных, производная суммы, произведения, частного функций; производная сложной функции, задачи на применение производной.
|
1
|
Фронтальный опрос, индивидуальный контроль
|
|
8
|
|
|
|
Умножение вектора на число
|
|
1
|
Фронтальный опрос. Индивидуальная работа по карточкам
|
|
|
|
ГЛАВА I.
МНОГОЧЛЕНЫ
|
|
|
10
|
|
|
9
|
|
|
Многочлены от одной переменной
|
|
Арифметические операции над многочленами от одной переменной
|
1
|
Фронтальный опрос, индивидуальный контроль
|
|
10
|
|
|
Теорема Безу
|
|
Арифметические операции над многочленами от одной переменной.
Деление многочлена на многочлен.
|
1
|
Фронтальный опрос, индивидуальный контроль
|
|
11
|
|
|
Схема Горнера
|
|
Арифметические операции над многочленами от одной переменной.
Деление многочлена на многочлен.
Разложение многочлена на множители
|
1
|
Фронтальный опрос, Индивидуальная работа, пары сменного состава
|
|
12
|
|
|
|
Компланарные векторы
|
|
1
|
Фронтальный опрос. Индивидуальная работа по карточкам. Самостоятельная работа обучающего характера
|
|
13
|
|
|
Многочлены от нескольких переменных.
|
|
Действия с многочленами.
Разложение многочленов на множители. Однородная и симметрическая системы
|
1
|
Индивидуальный контроль, коллективная работа
|
|
14
|
|
|
|
Компланарные векторы
|
Четырехугольник, параллелограмм, свойства параллелограмма
|
1
|
Фронтальный опрос. Индивидуальная работа у доски
|
|
15
|
|
|
Многочлены от нескольких переменных.
Однородные многочлены n-ой степени
|
|
Действия с многочленами.
Разложение многочленов на множители. Однородная и симметрическая системы
|
1
|
Фронтальный опрос, индивидуальный контроль
|
|
16
|
|
|
Симметрические и однородные многочлены
|
|
Действия с многочленами.
Разложение многочленов на множители. Однородная и симметрическая системы
|
1
|
Фронтальный опрос, дифференцированный контроль
|
|
17
|
|
|
Уравнения высших степеней
|
|
Способы решения уравнений степени выше второй
|
1
|
Фронтальный опрос, индивидуальный контроль
|
|
18
|
|
|
|
Зачет № 1
«Векторы в пространстве»
|
|
1
|
Проверочная работа
|
|
19
|
|
|
Уравнения высших степеней. Возвратные уравнения
|
|
Способы решения уравнений степени выше второй
|
1
|
Фронтальный опрос. Математический тест
|
|
|
|
|
|
Глава V. Метод координат в пространстве
|
|
15
|
|
|
20
|
|
|
|
Координаты точки
|
Прямоугольная система координат, ордината, абсцисса, аппликата, проекция на оси, на плоскости
|
1
|
Фронтальный опрос. Самостоятельная теоретическая работа
|
|
21
|
|
|
Контрольная работа №1 «Многочлены»
|
|
|
1
|
Контрольная работа
|
|
22
|
|
|
Анализ контрольной работы
|
|
|
1
|
Анализ контрольной работы
|
|
|
|
|
ГЛАВА 2. СТЕПЕНИ И КОРНИ. СТЕПЕННЫЕ ФУНКЦИИ
|
|
|
24
|
|
|
23
|
|
|
Понятие корня n-й степени из действительного числа
|
|
Определение корня n-ой степени четной и нечетной степени.
Решение иррациональных уравнений
|
1
|
Фронтальный опрос. Индивидуальная работа у доски
|
|
24
|
|
|
|
Координаты вектора
|
Вектор в пространстве; равенство векторов; правила выполнения действий над векторами; компланарные векторы; правило параллелепипеда
|
1
|
Фронтальный опрос. Самостоятельная теоретическая работа
|
|
25
|
|
|
Понятие корня n-й степени из действительного числа. Решение задач
|
|
Определение корня n-ой степени четной и нечетной степени.
Решение иррациональных уравнений
|
1
|
Фронтальный опрос. Математический диктант
|
|
26
|
|
|
|
Координаты вектора
|
Вектор в пространстве; равенство векторов; правила выполнения действий над векторами; компланарные векторы; правило параллелепипеда
|
1
|
Фронтальный опрос. Индивидуальная работа по карточкам
|
|
27
|
|
|
Функции 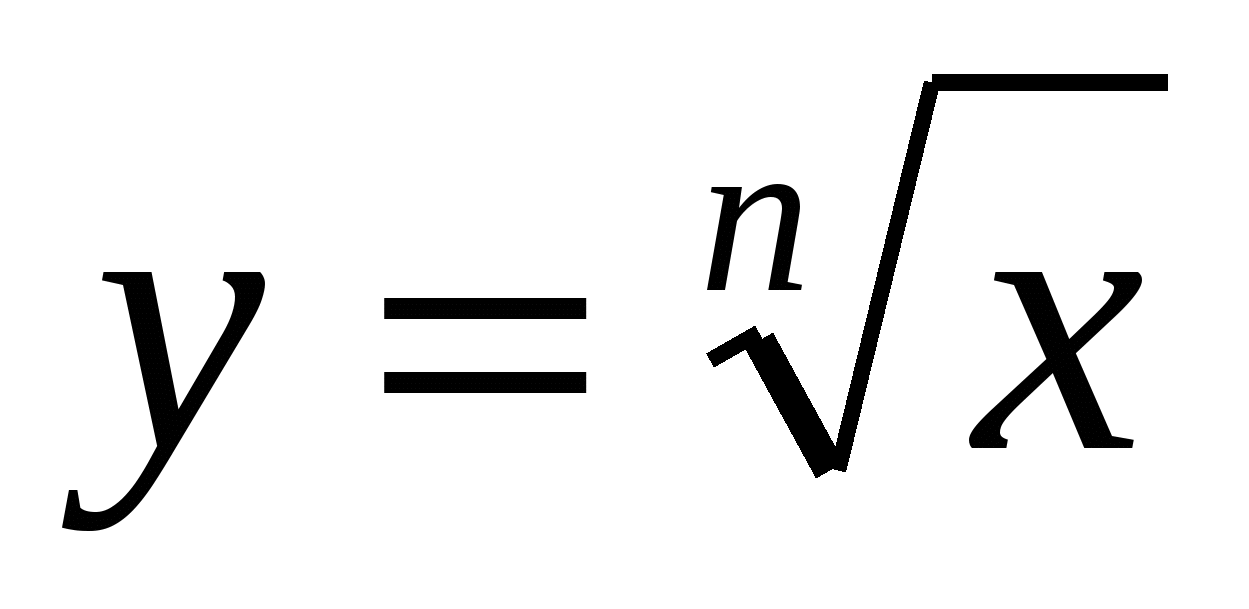 , их свойства и графики , их свойства и графики
|
|
Свойства функции 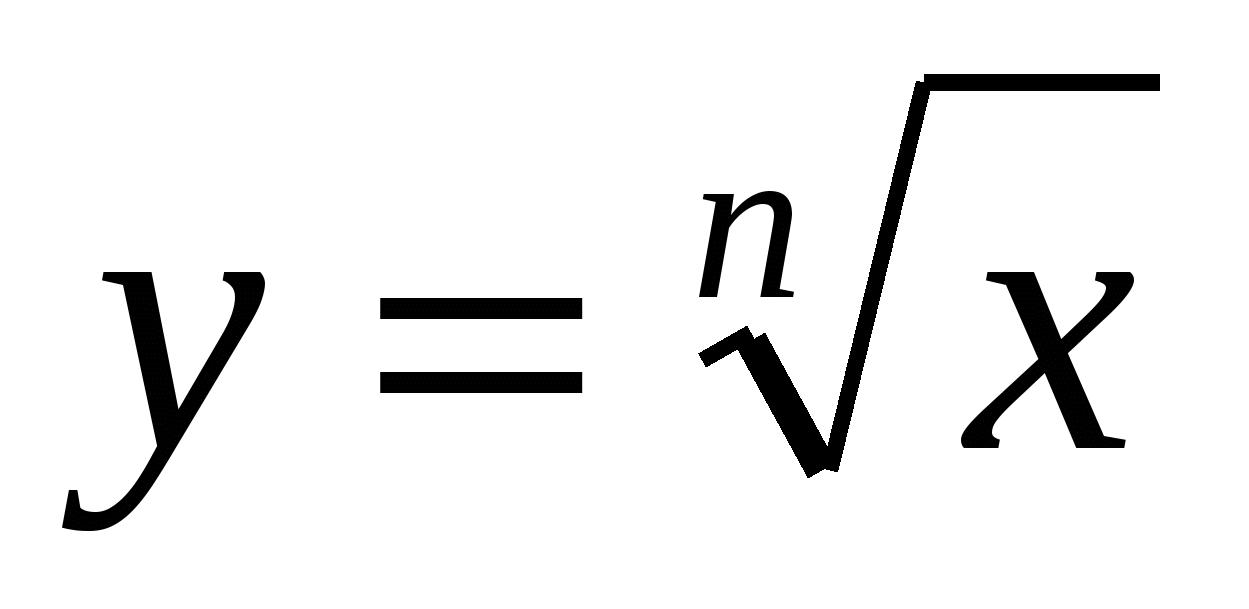 при четном и нечетном значении n. Построение графиков функций, содержащих корень n-ой степени при четном и нечетном значении n. Построение графиков функций, содержащих корень n-ой степени
|
1
|
Фронтальный опрос. Дифференцированный контроль
|
|
28
|
|
|
Функции 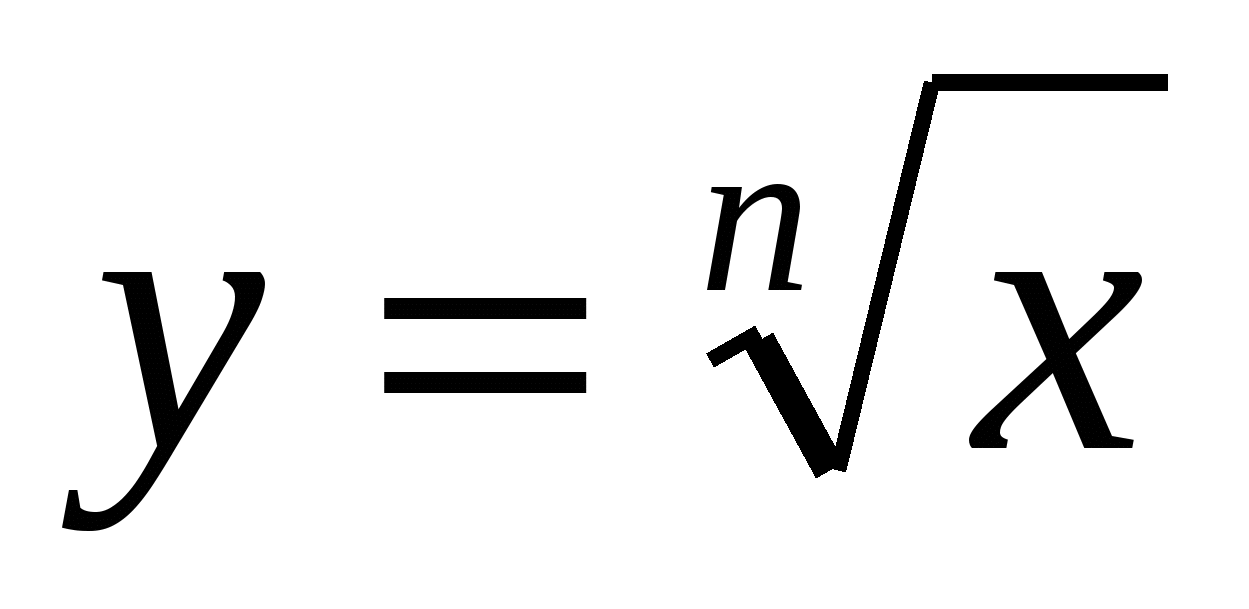 , их свойства и графики , их свойства и графики
|
|
Свойства функции 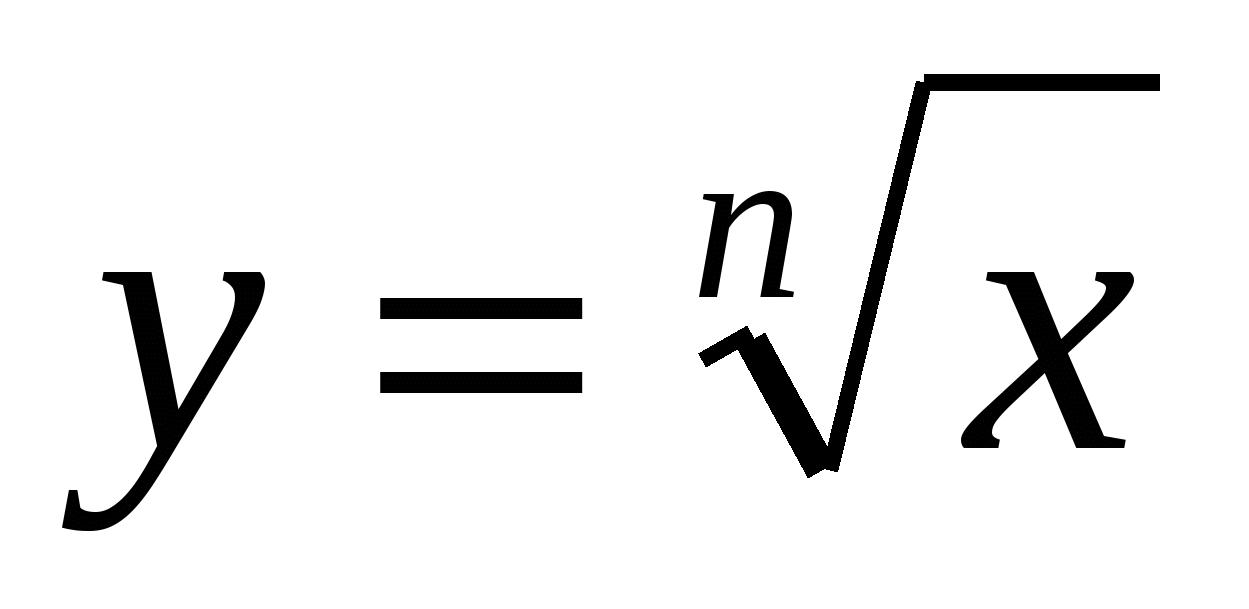 при четном и нечетном значении n. Построение графиков функций, содержащих корень n-ой степени при четном и нечетном значении n. Построение графиков функций, содержащих корень n-ой степени
|
1
|
Фронтальный опрос. Индивидуальная работа у доски
|
|
29
|
|
|
Исследование свойств функции 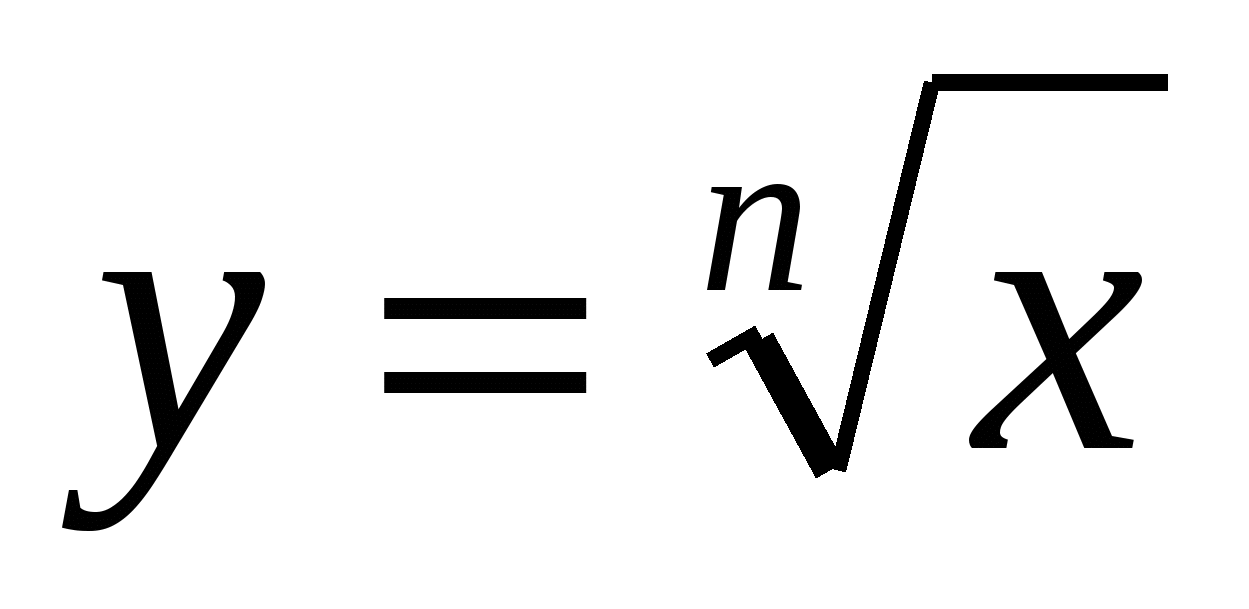 . Решение задач . Решение задач
|
|
1
|
Фронтальный опрос. Дифференцированный контроль
|
|
30
|
|
|
|
Связь между координатами векторов
и координатами точек
|
Декартовы координаты в пространстве, формулы координат вектора, связь между координатами векторов и координатами точек
|
1
|
Фронтальный опрос. Индивидуальная работа по карточкам. Самостоятельная работа обучающего характера
|
| |
31
|
|
|
Свойства корня n-й степени
|
|
Корень n-й степени, арифметический корень n-й степени, основные свойства
|
1
|
Фронтальный опрос. Индивидуальная работа у доски
|
|
32
|
|
|
|
Простейшие задачи в координатах
|
Декартовы координаты в пространстве, формулы координат вектора, связь между координатами векторов и координатами точек
|
1
|
Фронтальный опрос. Индивидуальная работа у доски
|
|
33
|
|
|
Свойства корня n-й степени
|
|
Корень n-й степени, арифметический корень n-й степени, основные свойства
|
1
|
Фронтальный опрос. Индивидуальный контроль
|
|
34
|
|
|
Свойств корня n-й степени. Вычисление иррациональных выражений
|
|
|
1
|
Фронтальный опрос. Индивидуальный контроль
|
|
35
|
|
|
Преобразование выражений, содержащих радикалы
|
|
Корень n-й степени, арифметический корень n-й степени, основные свойства, иррациональные уравнения и способы решения
|
1
|
Фронтальный опрос. Индивидуальная работа по карточкам
|
|
36
|
|
|
|
Простейшие задачи в координатах
|
Декартовы координаты в пространстве, формулы координат вектора, связь между координатами векторов и координатами точек
|
1
|
Фронтальный опрос. Индивидуальная работа у доски
|
| |
37
|
|
|
Преобразование выражений, содержащих радикалы
|
|
Иррациональные уравнения и способы решения
|
1
|
Индивидуальный контроль
|
| |
|
|
 Скачать 1.02 Mb.
Скачать 1.02 Mb. читель Антохина Е. А.
читель Антохина Е. А.