|
Согласно федеральному базисному учебному плану на изучение математики в 8 классе отводится не менее 175 часов из расчета 5 ч в неделю, при этом разделение часов на изучение алгебры и геометрии может быть следующим:
3 часа в неделю алгебры и 2 часа в неделю геометрии в течение всего учебного года, итого 105 часов алгебры и 70 часов геометрии.
ОСНОВНАЯ ЧАСТЬ
Тема 1. «Четырехугольники» (14 часов)
Раздел математики. Сквозная линия.
Геометрические фигуры и их свойства.
Измерение геометрических величин.
Обязательный минимум содержания образовательной области математика
Выпуклые многоугольники.
Сумма углов выпуклого многоугольника.
Параллелограмм, его свойства и признаки.
Прямоугольник, квадрат, ромб, их свойства и признаки.
Трапеция, средняя линия трапеции; равнобедренная трапеция.
Теорема Фалеса.
Требования к математической подготовке
Уровень обязательной подготовки обучающегося
Знать различные виды четырехугольников, их признаки и свойства.
Уметь применять свойства четырехугольников при решении простых задач.
Уровень возможной подготовки обучающегося
Уровень обязательной подготовки выпускника
Меньшая сторона прямоугольника равна 6 см. Найдите длины диагоналей, если они пересекаются под углом 600.
Уровень возможной подготовки выпускника
В параллелограмме ABCD проведена биссектриса угла А, которая пересекает сторону ВС в точке F. Докажите, что треугольник АВF равнобедренный
Постройте прямоугольник по стороне и диагонали.
Тема 2. «Площади фигур» (14 часов)
Раздел математики. Сквозная линия.
Геометрические фигуры и их свойства.
Измерение геометрических величин.
Обязательный минимум содержания образовательной области математика
Понятие о площади плоских фигур.
Равносоставленные и равновеликие фигуры.
Площадь прямоугольника.
Площадь параллелограмма.
Площадь треугольника.
Площадь трапеции.
Теорема Пифагора
Требования к математической подготовке
Уровень обязательной подготовки обучающегося
Уметь пользоваться языком геометрии для описания предметов окружающего мира.
Уметь вычислять значения площадей основных геометрических фигур и фигур, составленных из них;
Знать формулы вычисления геометрических фигур, теорему Пифагора и уметь применять их при решении задач.
Уметь выполнять чертежи по условию задач
Уровень возможной подготовки обучающегося
Знать формулы вычисления геометрических фигур, теорему Пифагора и уметь применять их при решении задач.
Уметь решать геометрические задачи, опираясь на изученные свойства фигур и отношений между ними, применяя дополнительные построения, алгебраический аппарат, идеи симметрии.
Уметь решать задачи на доказательство и использовать дополнительные формулы для нахождения площадей геометрических фигур.
Уровень обязательной подготовки выпускника
Найдите площадь равнобокой трапеции, если ее основания равны 12 см и 6 см, а боковая сторона образует с одним из оснований угол, равный 450.
В прямоугольнике ABCD найдите AD, если АВ = 5, АС = 13.
Уровень возможной подготовки выпускника
В ромбе высота, равная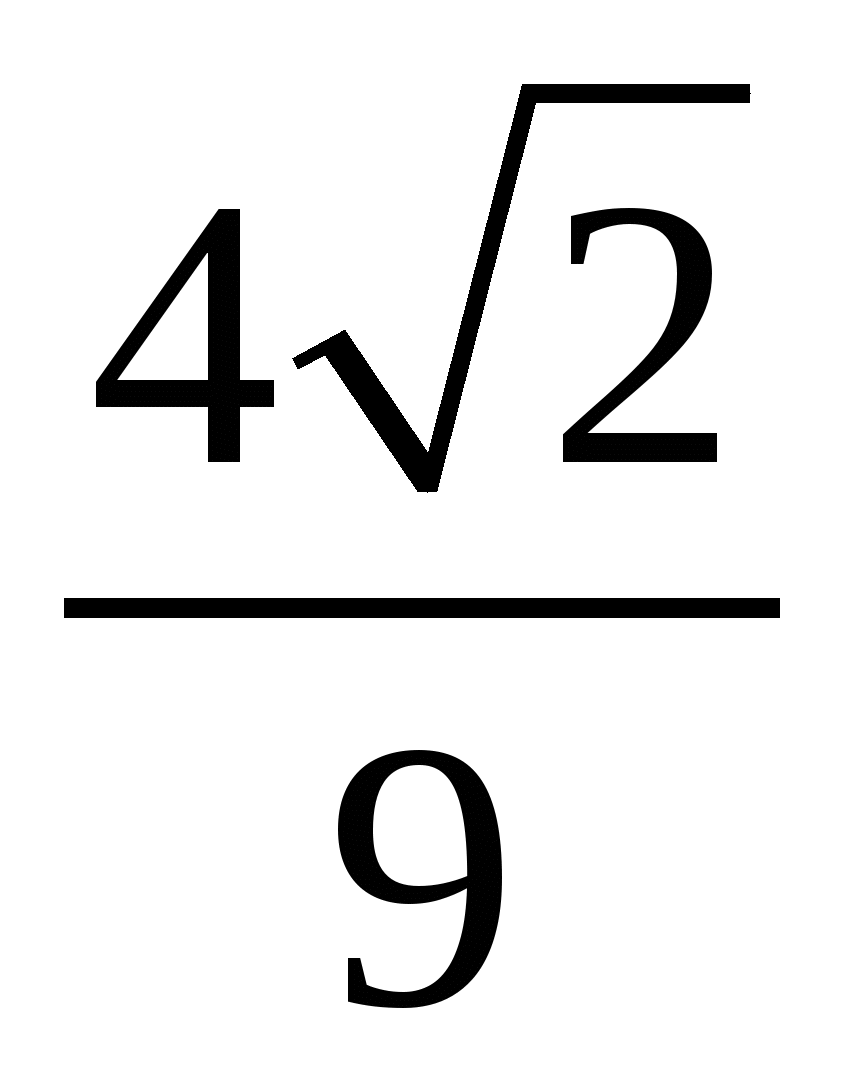 см, составляет см, составляет 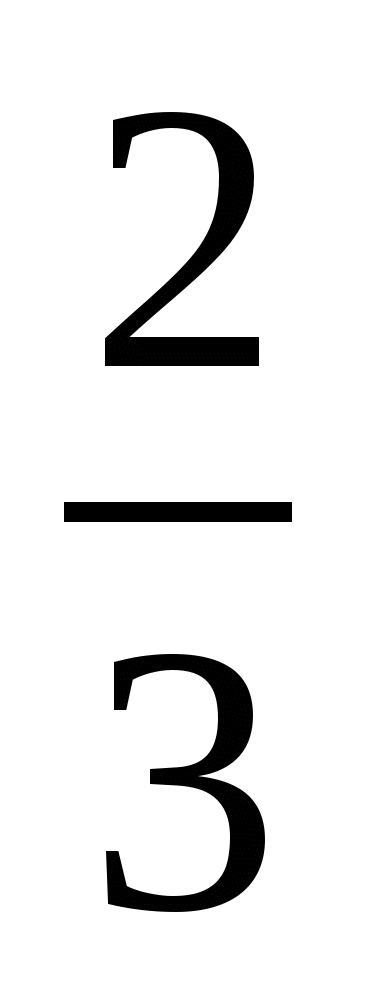 большей диагонали. Найдите площадь ромба. большей диагонали. Найдите площадь ромба.
В равнобедренном треугольнике АВС с основанием ВС высота АD равна 8 см. Найдите площадь треугольника АВС, если медиана DM треугольника АDС равна 8 см.
Тема 3. «Подобные треугольники» (20 часов)
Раздел математики. Сквозная линия.
Геометрические фигуры и их свойства.
Измерение геометрических величин.
Обязательный минимум содержания образовательной области математика
Подобие треугольников; коэффициент подобия.
Признаки подобия треугольников.
Связь между площадями подобных фигур.
Синус, косинус, тангенс, котангенс острого угла прямоугольного треугольника.
Решение прямоугольных треугольников.
Основное тригонометрическое тождество.
Требования к математической подготовке
Уровень обязательной подготовки обучающегося
Знать определение подобных треугольников.
Уметь применять подобие треугольников при решении несложных задач.
Уметь пользоваться языком геометрии для описания предметов окружающего мира.
Уметь распознавать геометрические фигуры, различать их взаимное расположение.
Уметь изображать геометрические фигуры.
Уметь выполнять чертежи по условию задач.
Знать признаки подобия треугольников, уметь применять их для решения практических задач.
Уметь находить синус, косинус, тангенс и котангенс острого угла прямоугольного треугольника.
Уровень возможной подготовки обучающегося
Уметь решать геометрические задачи, опираясь на изученные свойства фигур и отношений между ними.
Уметь применять признаки подобия треугольников для решения практических задач.
Уметь проводить доказательные рассуждения при решении задач, используя известные теоремы.
Уметь решать геометрические задачи на соотношения между сторонами и углами прямоугольного треугольника.
Уровень обязательной подготовки выпускника
В трапеции ABCD проведены диагонали АС и ВD, которые пересекаются в точке О. Докажите, что треугольник СОВ подобен треугольнику AOD.
Уровень возможной подготовки выпускника
Докажите, что середины сторон ромба являются вершинами прямоугольника.
Постройте треугольник, если даны середины его сторон.
Биссектрисы MD и NK треугольника MNP пересекаются в точке О. Найдите отношение ОК:ON, если MN = 5 см, NP = 3 см, MP = 7 см.
Тема 4. «Окружность»
(17 часов)
Раздел математики. Сквозная линия
Геометрические фигуры и их свойства.
Измерение геометрических величин.
Обязательный минимум содержания образовательной области математика
Центральный, вписанный угол; величина вписанного угла.
Взаимное расположение прямой и окружности.
Касательная и секущая к окружности.
Равенство касательных, проведенных из одной точки.
Замечательные точки треугольника: точки пересечения серединных перпендикуляров, биссектрис, медиан.
Окружность, вписанная в треугольник.
Окружность, описанная около треугольника.
Требования к математической подготовке
Уровень обязательной подготовки обучающегося
Уметь вычислять значения геометрических величин.
Знать свойства биссектрисы угла и серединного перпендикуляра к отрезку.
Уметь распознавать геометрические фигуры, различать их взаимное расположение.
Уметь решать задачи на построение.
Уровень возможной подготовки обучающегося
Уметь решать геометрические задачи, опираясь на изученные свойства фигур и отношений между ними.
Уметь проводить доказательные рассуждения при решении задач, используя известные теоремы.
Знать метрические соотношения в окружности: свойства секущих, касательных, хорд и уметь применять их в решении задач.
Иметь понятие о вписанных и описанных четырехугольниках.
Уровень обязательной подготовки выпускника
Окружность разделена на две дуги, причем градусная мера одной из них в три раза больше градусной меры другой. Чему равны центральные углы, соответствующие этим дугам?
Через точку А окружности проведены диаметр АС и две хорды АВ и AD, равные радиусу этой окружности. Найдите углы четырехугольника АВСD и градусные меры дуг АВ, ВС, CD, AD.
Уровень возможной подготовки выпускника
К данной окружности постройте касательную, проходящую через данную точку вне окружности.
Биссектрисы углов при основании АВ равнобедренного треугольника АВС пересекаются в точке М. Докажите, что прямая СМ перпендикулярна к прямой АВ.
В окружность вписан равнобедренный треугольник АВС с основанием ВС. Найдите углы треугольника, если 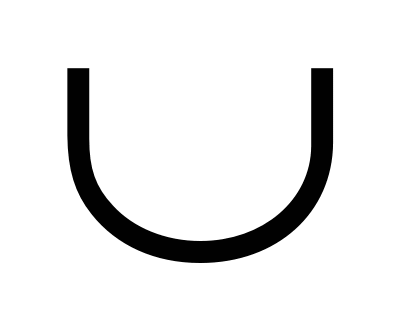 ВС =1020 . ВС =1020 .
Тема 5. «Повторение. Решение задач» (5 часов)
Раздел математики. Сквозная линия.
Геометрические фигуры и их свойства.
Измерение геометрических величин.
Обязательный минимум содержания образовательной области математика
Площадь треугольника, четырехугольников.
Теорема Пифагора
Подобие треугольников; коэффициент подобия.
Признаки подобия треугольников.
Решение прямоугольных треугольников.
Окружность.
Построения с помощью циркуля и линейки. Основные задачи на построение.
Требования к математической подготовке
Уровень обязательной подготовки обучающегося
Уметь пользоваться языком геометрии для описания предметов окружающего мира.
Уметь распознавать геометрические фигуры, различать их взаимное расположение.
Уметь изображать геометрические фигуры.
Уметь выполнять чертежи по условию задач.
Уметь доказывать теоремы о параллельности прямых с использованием соответствующих признаков.
Уметь вычислять значения геометрических величин (длин, углов, площадей).
Уметь решать задачи на построение.
Уровень возможной подготовки обучающегося
Уметь решать геометрические задачи, опираясь на изученные свойства фигур и отношений между ними.
Уметь проводить доказательные рассуждения при решении задач, используя известные теоремы.
Уровень обязательной подготовки выпускника
В равнобедренной трапеции диагональ равна 10 см, а высота равна 6 см. Найдите площадь трапеции.
Два угла треугольника равны 450 и 300. Найдите отношения противолежащих им сторон.
Две окружности с центрами в точках О и О1 и равными радиусами пересекаются в точках А и В. Докажите, что четырехугольник АО1ВО – параллелограмм.
Уровень возможной подготовки выпускника
В треугольнике АВС преведена высота ВН. Докажите, что если:
а) угол А острый, то  ; ;
б) угол А тупой, то 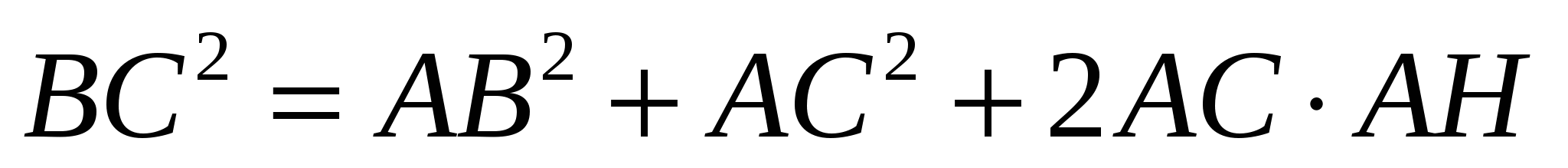 . .
Найдите радиус вписанной в равносторонний треугольник окружности, если радиус описанной окружности равен 10 см.
УЧЕБНО-КАЛЕНДАРНОЕ ПЛАНИРОВАНИЕ
в 8 классе по геометрии
№
урока
|
Содержание учебного материала
|
№ п/п
|
Сроки
|
|
Четырехугольники (14 часов)
|
|
|
1
|
Многоугольники. Выпуклые многоугольники. Периметр многоугольника.
|
п.39-40
|
|
2
|
Четырехугольник. Сумма углов выпуклого многоугольника, четырехугольника.
|
п.41
|
|
3
|
Параллелограмм. Свойства параллелограмма.
|
п.42
|
|
4
|
Признаки параллелограмма.
|
п.43
|
|
5
|
Решение задач по теме «Параллелограмм»
|
п.43
|
|
6
|
Трапеция, равнобедренная трапеция.
|
п.44
|
|
7
|
Теорема Фалеса.
|
Зад.385
|
|
8
|
Задачи на построение. Деление отрезка на n равных частей.
|
Зад. 396
|
|
9
|
Прямоугольник, его свойства и признаки.
|
п.45
|
|
10
|
Ромб, квадрат; их свойства и признаки.
|
п.46
|
|
11
|
Решение задач по теме «Прямоугольник, ромб, квадрат»
|
п.42-46
|
|
12
|
Осевая и центральная симметрии. Симметрия фигур.
|
п.47
|
|
13
|
Урок повторения и обобщения по теме «Четырехугольники»
|
п.39-47
|
|
14
|
Контрольная работа№1 «Четырехугольники»
|
|
|
|
Площади фигур (14часов)
|
|
|
15
|
Понятие о площади плоских фигур. Равносоставленные и равновеликие фигуры. Площадь многоугольника.
|
п.48-49
|
|
16
|
Площадь квадрата и прямоугольника.
|
п.50
|
|
17
|
Площадь параллелограмма. Площадь четырехугольника.
|
п.51
|
|
18
|
Площадь треугольника. Площадь прямоугольного треугольника.
|
п.52
|
|
19
|
Площадь треугольника. Формула Герона.
|
п.52
|
|
20
|
Площадь трапеции.
|
п.53
|
|
21
|
Решение задач на вычисление площадей фигур (основные формулы)
|
п.49-53
|
|
22
|
Решение задач на нахождение площадей фигур.
|
п.49-53
|
|
23
|
Теорема Пифагора.
|
п.54
|
|
24
|
Теорема, обратная теореме Пифагора.
|
п.55
|
|
25
|
Решение задач по теме «Теорема Пифагора»
|
п.54-55
|
|
26
|
Решение задач на нахождение площадей с помощью микрокалькулятора.
|
№524-531
|
|
27
|
Повторительно-обобщающий урок.
|
п.49-53
|
|
28
|
Контрольная работа №2 «Площади фигур»
|
|
|
|
Подобные треугольники (20 часов)
|
|
|
29
|
Пропорциональные отрезки. Определение подобных треугольников, коэффициент подобия.
|
п.56-57
|
|
30
|
Связь между площадями подобных фигур.
|
п.58
|
|
31
|
Первый признак подобия треугольников.
|
п.59
|
|
32
|
Решение задач на применение первого признака подобия треугольников.
|
п.59
|
|
33
|
Второй и третий признаки подобия треугольников.
|
п.60-61
|
|
34
|
Решение задач на применение признаков подобия треугольников.
|
п.59-61
|
|
35
|
Решение задач на применение признаков подобия треугольников.
|
п.59-61
|
|
36
|
Контрольная работа №3 «Признаки подобия треугольников»
|
|
|
37
|
Средняя линия треугольника.
|
п.62
|
|
38
|
Средняя линия треугольника. Свойство медиан треугольника
|
п.62
|
|
39
|
Пропорциональные отрезки в прямоугольном треугольнике. Понятие среднее геометрическое.
|
п.63
|
|
40
|
Пропорциональные отрезки в прямоугольном треугольнике. Решение задач.
|
п.63
|
|
41
|
Практические приложения подобия треугольников. Задачи на построение.
|
п.64
|
|
42
|
Измерительные работы на местности. Подобие произвольных фигур.
|
п.64
|
|
43
|
Решение задач по теме « Применение подобия к доказательству теорем и решению задач»
|
п.62-65
|
|
44
|
Синус, косинус и тангенс острого угла прямоугольного треугольника. Основное тригонометрическое тождество.
|
п.66
|
|
45
|
Значения синуса, косинуса ,тангенса и котангенса для углов 30,40 и 60 градусов.
|
п.67
|
|
46
|
Соотношения между сторонами и углами прямоугольного треугольника. Решение прямоугольных треугольников.
|
п.63-67
|
|
47
|
Решение прямоугольных треугольников.
|
п.66-67
|
|
48
|
Контрольная работа №4 «Средняя линия треугольника. Соотношения между сторонами и углами прямоугольного треугольника»
|
|
|
|
Окружность (17 часов)
|
|
|
49
|
Окружность Центр, радиус, диаметр. Взаимное расположение прямой и окружности, двух окружностей.
|
п.68
|
|
50
|
Касательная и секущая к окружности; равенство касательных, проведенных из одной точки.
|
П.69
|
|
51
|
Касательная к окружности. Решение задач.
|
П.69
|
|
52
|
Дуга и хорда. Градусная мера дуги окружности. Центральный угол.
|
П.70
|
|
53
|
Теорема о вписанном угле и ее следствия. Соответствие между величиной угла и длиной дуги окружности.
|
П.71
|
|
54
|
Метрические соотношения в окружности: свойства секущих, касательных, хорд.
|
П.71
|
|
55
|
Решение задач по теме «Центральные и вписанные углы»
|
п.70-71
|
|
56
|
Замечательные точки треугольника: точки пересечения серединных перпендикуляров,биссектрис,медиан.
|
п.72
|
|
57
|
Серединный перпендикуляр к отрезку. Теорема о серединном перпендикуляре и ее применение при решении задач.
|
п.72
|
|
58
|
Теорема о точке пересечения высот треугольника.
|
п.73
|
|
59
|
Вписанная окружность.Окружность вписанная в треугольник.
|
п.74
|
|
60
|
Свойство описанного четырехугольника.
|
п.74
|
|
61
|
Описанная окружность. Окружность описанная около треугольника.
|
п.75
|
|
62
|
Свойство вписанного четырехугольника.
|
п.75
|
|
63
|
Повторительно-обобщающий урок по теме «Окружность»
|
п.68-74
|
|
64
|
Повторительно-обобщающий урок по теме «Окружность»
|
п.68-74
|
|
65
|
Контрольная работа №5 «Окружность»
|
|
|
|
Повторение (5 часов)
|
|
|
66
|
Итоговое повторение. Четырехугольники.
|
|
|
67
|
Итоговое повторение. Площади фигур.
|
|
|
68
|
Итоговое повторение. Площади фигур.
|
|
|
69
|
Итоговое повторение. Соотношения между сторонами и углами прямоугольного треугольника.
|
|
|
70
|
Итоговое повторение. Подобие треугольников.
|
|
|
|
Итого: 70 часов
|
|
Литература
1.Атанасян Л.С. Геометрия 7 – 9. Учебник для 7 – 9 классов средней школы. М., «Просвещение», 2008.
2.Бурмистрова Т.А. Геометрия 7 - 9 классы. Программы общеобразовательных учреждений. М., «Просвещение», 2009.
3.Стандарт основного общего образования по математике//«Вестник образования» -2004 - № 12 - с.107-119.
Электронные учебные пособия
Уроки геометрии в 7 – 9 классе
9 КЛАСС
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
КУРСА «ГЕОМЕТРИЯ» 9 КЛАСС
Рабочая программа по геометрии для обучающихся 9 класса составлена на основе федерального компонента государственного стандарта основного общего образования с учетом примерной программы курса геометрии для 9 классов средней общеобразовательной школы, рекомендованной Департаментом образовательных программ и стандартов общего образования Министерства образования Российской Федерации от 2004 года.
Согласно Федеральному базисному учебному плану для общеобразовательных учреждений РФ для изучения курса геометрии в 9 классе отводится 2 часа в неделю, 70 часов в год федерального компонента. Программа обеспечивает обязательный минимум подготовки учащихся по геометрии, определяемый образовательным стандартом, соответствует общему уровню развития и подготовки учащихся данного возраста.
Изучение базового курса ориентировано на использование учебника «Геометрия 7-9» автора Л.С.Атанасян, рекомендованного Министерством образования и науки Российской Федерации. Для организации самостоятельной, практической, контрольных, домашних работ используются «Дидактические карточки – задания по геометрии 9 класс» Т.М.Мищенко, Зив, Б. Г. Дидактические материалы по геометрии для 9 кл. - М.: Просвещение, 2005, а также методическое пособие «Поурочные разработки по геометрии 9 класса» Атанасян, Л. С, Изучение геометрии в 7-9 классах: методические рекомендации для учителя Л. С. Атанасян. - М.: Просвещение, 2005.
Целью данного пособия является помощь учителю в планировании и подготовке уроков геометрии в 9 классе.
Программа направлена на достижение следующих целей:
овладение системой математических знаний и умений, необходимых для применения практической деятельности изучения смежных дисциплин, продолжения образования;
интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе: ясность и точность мысли, критичность мышления, интуиция, логическое мышление, элементы алгоритмической культуры, пространственных представлений;
формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов;
воспитание культуры личности, отношения к математике как части общечеловеческой культуры, понимание значимости математики для научно технического прогресса;
развитие представлений о полной картине мира, о взаимосвязи математики с другими предметами.
В ходе обучения геометрии по данной программе с использованием учебника и методического пособия для учителя, решаются следующие задачи:
систематическое изучение свойств геометрических фигур на плоскости;
формирование пространственных представлений; развитие логического мышления и подготовка аппарата для изучения смежных дисциплин (физика, черчение и др.) и курса стереометрии в старших классах;
овладение конкретными знаниями необходимыми для применения в практической деятельности.
В основу курса геометрии для 9 класса положены такие принципы как:
Целостность и непрерывность, означающие, что данная ступень является важным звеном единой общешкольной подготовки по математике.
Научность в сочетании с доступностью, строгость и систематичность изложения (включение в содержание фундаментальных положений современной науки с учетом возрастных особенностей обучаемых
Практико-ориентированность, обеспечивающая отбор содержания, направленного на решение простейших практических задач планирования деятельности, поиска нужной информации.
Принцип развивающего обучения (обучение ориентировано не только на получение новых знаний, но и активизацию мыслительных процессов, формирование и развитие у школьников обобщенных способов деятельности, формирование навыков самостоятельной работы).
Место предмета в федеральном базисном учебном плане Согласно федеральному базисному учебному плану для образовательных учреждений Российской Федерации на изучение геометрии в 9 классе отводится 2 ч в неделю, всего 70 ч.
В том числе: Контрольных работ – 5 часов, которые распределены по разделам следующим образом: «Метод координат» 1 час, «Соотношение между сторонами и углами треугольника» 2 часа, «Длина окружности и площадь круга» 1 час, «Движения» 1 час и 1 час на итоговую административную контрольную работу.
Данное планирование определяет достаточный объем учебного времени для повышения математических знаний учащихся в среднем звене школы, улучшения усвоения других учебных предметов.
Промежуточная аттестация проводится в форме тестов, самостоятельных, проверочных работ и математических диктантов (по 10 - 15 минут) в конце логически законченных блоков учебного материала. Итоговая аттестация предусмотрена в виде административной контрольной работы.
Уровень обучения – базовый.
Требования к уровню подготовки учащихся
В курсе геометрии 9-го класса формируется понятие вектора. Особое внимание уделяется выполнению операций над векторами в геометрической форме. Учащиеся дополняют знания о треугольниках сведениями о методах вычисления элементов произвольных треугольниках, основанных на теоремах синусов и косинусов. Даются систематизированные сведения о правильных многоугольниках, об окружности, вписанной в правильный многоугольник и описанной. Особое место занимает решение задач на применение формул. Даются первые знания о движении, повороте и параллельном переносе. Серьезное внимание уделяется формированию умений рассуждать, делать простые доказательства, давать обоснования выполняемых действий. Параллельно закладываются основы для изучения систематических курсов стереометрии, физики, химии и других смежных предметов.
В результате изучения курса геометрии 9-го класса учащиеся должны уметь:
пользоваться геометрическим языком для описания предметов окружающего мира;
распознавать геометрические фигуры, различать их взаимное расположение;
изображать геометрические фигуры; выполнять чертежи по условию задач; осуществлять преобразование фигур;
вычислять значения геометрических величин (длин, углов, площадей), в том числе: определять значение тригонометрических функций по заданным значениям углов; находить значения тригонометрических функций по значению одной из них; находить стороны, углы и площади треугольников, дуг окружности, площадей основных геометрических фигур и фигур, составленных из них;
решать геометрические задания, опираясь на изученные свойства фигур и отношений между ними, применяя дополнительные построения, алгебраический и тригонометрический аппарат, соображения симметрии;
проводить доказательные рассуждения при решении задач, используя известные теоремы, обнаруживая возможности для их использования;
решать простейшие планиметрические задачи в пространстве.
Для реализации данной программы используются педагогические технологии уровневой дифференциации обучения, технологии на основе личностной ориентации, которые подбираются для каждого конкретного класса, урока, а также следующие методы и формы обучения и контроля:
Формы работы: фронтальная работа; индивидуальная работа; коллективная работа; групповая работа.
Методы работы: рассказ; объяснение, лекция, беседа, применение наглядных пособий; дифференцированные задания, самостоятельная работа; взаимопроверка, дидактическая игра; решение проблемно-поисковых задач.
Используются следующие формы и методы контроля усвоения материала: устный контроль (индивидуальный опрос, устная проверка знаний); письменный контроль (контрольные работы, письменный зачет, графические диктанты, тесты); лабораторно-практический контроль (контрольно-лабораторные работы, практические работы). Учебный процесс осуществляется в классно-урочной форме в виде комбинированных, контрольно-проверочных и др. типов уроков
ОСНОВНАЯ ЧАСТЬ
|
|
|
 Скачать 0.76 Mb.
Скачать 0.76 Mb.