Применение производной к исследованию функции в решении задач при подготовке к егэ. 11 класс
 Скачать 63.26 Kb.
|
| МАОУ Тунгусовская СОШ. Естественнонаучное направление. Тема: Применение производной к исследованию функции в решении задач при подготовке к ЕГЭ. 11 класс. Манькова Ирина Геннадьевна, учитель математики Манькова Ирина Геннадьевна, учитель математики МАОУ Тунгусовская СОШ. Естественнонаучное направление. Тема: Применение производной к исследованию функции в решении задач при подготовке к ЕГЭ. 11 класс. Цели урока:
Тип урока: урок итогового повторения. Оборудование урока: мультимедийный проектор, слайды, созданные в программе Microsoft Power Point, набор тестовых заданий по теме «Производная функции», контрольные оценочные листы, набор карточек с цифрами. Ход урока: I. Организационный момент (1 мин). II. Объявление темы урока, постановка цели и задач (2 мин) III. Актуализация опорных знаний:
IV. Разминка – устные упражнения (10 мин). Презентация. V. Отработка навыков. Письменные упражнения (с обсуждением и последующей проверкой) (26 мин).
VI. Дифференцированное домашнее задание (2 мин). VII. Итог урока (1 мин). Ход урока.I. Организационный момент Проверяется подготовленность классного помещения и готовность учащихся к уроку. II. Объявление темы урока, постановка цели и задач Учащимся сообщается тема урока и цели, подчеркивается актуальность повторения данной темы для подготовки к ЕГЭ. Учитель: Ребята, я предлагаю девизом нашего сегодняшнего урока сделать замечательные слова профессора Нойгауза: «Знание, добытое без личного усилия, без личного напряжения, - знание мертвое. Только пропущенное через собственную голову становится твоим достоянием». Наши знания должны работать и принести положительный результат на экзамене. Сегодня каждый из вас проведет диагностику своих знаний по данной теме, для этого у вас имеются оценочные листы, в которых вы оцените свои знания и возможности по каждому из разделов. В соответствии с этой оценкой на индивидуальных консультациях мы постараемся устранить имеющиеся пробелы. III. Актуализация опорных знаний: Начинаем работу с повторения теоретического материала (приложение 2). Учащимся предлагается выполнить небольшую работу (вставьте пропущенное математическое понятие) с последующей проверкой. Учащиеся проговаривают каждое правило. Учитель акцентирует внимание учащихся на грамотности математической речи. 1. Если функция ƚ(х) дифференцируема на интервале (а;в) и ƚ´(х)>0 для всех х€(а;в), то функция ------------------- на интервале (а;в). 2. Если функция ƚ(х) дифференцируема на интервале (а;в) и ƚ´(х)-----0 для всех х€(а;в), то функция убывает на интервале (а;в). 3. Пусть функция ƚ(х) дифференцируема на интервале (а;в), х˳€(а;в) и ƚ´( х˳)=0. Тогда если при переходе через стационарную точку х˳ функции ƚ(х) её производная меняет знак с «+» на «-», то точка х˳ - точка --------------- функции ƚ(х). 4. Если функция ƚ(х) непрерывна в точке х˳ и производная в этой точке меняет знак с « ----» на «----», то точка х˳ - точка минимума. 5. Если х˳- точка экстремума функции ƚ(х), то производная в этой точке равна------. 6. Точки, в которых производная функции равна 0, называется--------. Верно 6 заданий - оценка «5» 5 заданий - оценка «4» 3-4 задания - оценка «3» 1-2 задания – оценка «2» Оценку выставляют в оценочный лист. IV. Устная работа – разминка. приложение 1 На экране появляется слайд «Устные упражнения». Учащиеся применяют теорию на практике. Выполняя устные упражнения, учащиеся показывают ответ с помощью карточек с цифрами. Учитель обращает внимание на речь учащихся. Верно 11-12 заданий - оценка «5» 8-10 заданий - оценка «4» 5-7 задания - оценка «3» 1-4 задания – оценка «2» Оценку выставляют в оценочный лист. V. Отработка навыков. Письменные упражнения: один ученик работает за доской. (с обсуждением и последующей проверкой. 1.а) Учащимся предлагается задание: найдите значение производной функции в данной точке.  ,  . Учащиеся выполняют задание самостоятельно, один ученик работает за доской (с обсуждением и последующей проверкой). Учитель, проходя между рядами, наблюдает за деятельностью учащихся и при необходимости корректирует их. Решение объясняет ученик, работавший за доской, ученики сверяют своё решение с решением на доске и по необходимости задают вопросы. Решение. ,   Ответ: 0.б) Работа немного усложняется. Работа проходит у доски с комментарием. Предлагается задание: найдите те значения аргумента, при котором значение производной равно нулю. Решите уравнение  если f(x)=cos5xcos3x+sin5xsin3xРешение. f(x)=cos5xcos3x+sin5xsin3x f(x)=cos2x ƚ´(х)=-2sin2x ƚ´(х)=0 -2sin2x=0 sin2x=0 2x=¶n, n€Z; x=¶n/2, n€Z Ответ: x=¶n/2, n€Z 2) Самостоятельная работа (приложение3)с последующей самопроверкой. Предлагается задание: по графику производной функции опишите свойства функции на отрезке [-2;5]. По цепочке ученики комментируют свой ответ. 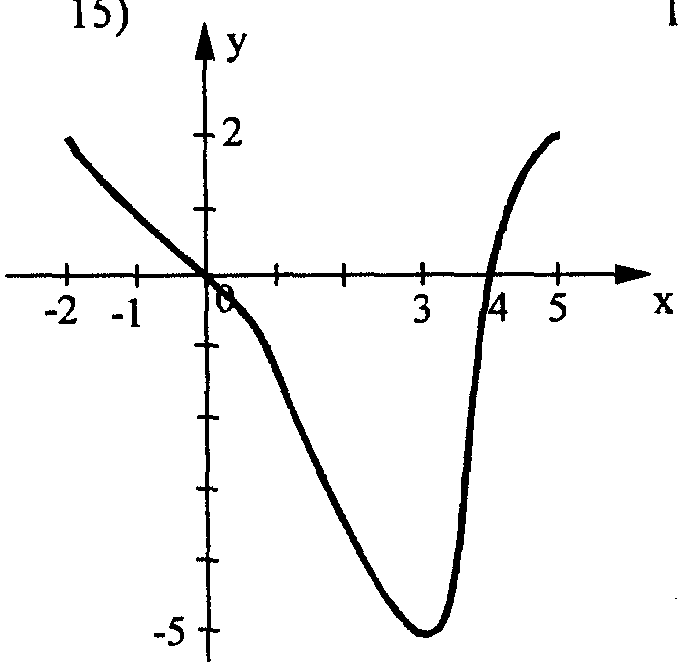 1) Возрастает на промежутке 2) Убывает на промежутке 3) Имеет максимум 4) Имеет минимум 5)Наибольшая длина промежутка возрастания равна 6) Длина промежутка убывания равна Верно 6 заданий - оценка «5» 5 заданий - оценка «4» 3-4 задания - оценка «3» 1-2 задания – оценка «2» Оценку выставляют в оценочный лист 3) Работа в группах – отчёт каждой группы у доски. 1 группа: Найдите промежутки монотонности и точки экстремума у = х4 – 2х³ – 3 2 группа: Найдите наибольшее и наименьшее значение функции на отрезке у = х³ - 27 х + 11. [0;4] 4) Тест с последующей самопроверкой (приложение4). После окончания работы учащиеся сдают тест на отдельных листочках, оставив при этом для проверки номера выбранных ответов. Далее учащимся предоставляется возможность проверить и оценить свою работу. Ключ записан на доске (21423) 1. Найдите производную функции у=3cosх+х² 1) у´=3sinх-2х 2) у´=2х-3sinх 3) у´= 2х+3 sinх 4) у´= -3cosх+2х 2. Найдите значение производной функции у= 6√х+2х-4 в точке х =9 1) 3 2) 10 3) 5 4) -1 3. Найдите длину промежутка убывания функции у= х³-75х+23 1) -5 2) 5 3) 0 4)10 4. Найдите точку максимума функции у= х³-75х+23 1) 5 2) -5 3) 0 4) 25 5. Найдите наименьшее значение функции у=х³-3х+19 на отрезке [ -2;0] 1) 21 2) 19 3) 17 4) 15 Верно 5 заданий - оценка «5» 4 заданий - оценка «4» 3 задания - оценка «3» 1-2 задания – оценка «2» Оценку выставляют в оценочный лист VI. Дифференцированное домашнее задание (2 мин). Все учащиеся класса получают задание из учебника стр.171 № 3(3). Дополнительно: ученикам, получивших за тест оценку «5», выдается дополнительное задание на карточке; ученики, допустившие ошибки в тесте, делают работу над ошибками VII. Итог урока. Рефлексия. Ребята, вы выставили себе оценки за каждую самостоятельную работу в оценочный лист. Найдите средний балл, это есть результат вашей работы на уроке (приложение 5). Довольны ли вы собой, своей работой? Поднимите, пожалуйста, руку те, чей средний балл “5” или “4”. Это результат хороший. Ребята, а с теми из вас, кто не доволен результатами своей работы по данной теме, у кого есть вопросы, мы с вами встречаемся на дополнительном занятии. Приложения к уроку Приложение № 1 – презентация Приложение № 2 – оценочный лист
|