Учитель математики высшей квалификационной категории Марина Геннадьевна Важенина
 Скачать 360.81 Kb. Скачать 360.81 Kb.
|
| Учитель математики высшей квалификационной категории Марина Геннадьевна Важенина  Учитель математики высшей квалификационной категории Марина Геннадьевна Важенина
С момента создания традиционной классно-урочной системы обучения, всегда существовала проблема формирования у обучаемых высокой и устойчивой мотивации к обучению, активной познавательной деятельности, а также проблема поиска наиболее эффективных методов и средств организации образовательного процесса. Как правило, выбираемый учителем средний темп работы на уроке оказывается нормальным лишь для определённой части учеников, для других он слишком быстрый, для третьих излишне замедленный. Одна и та же учебная задача для одних детей является сложной, почти неразрешимой проблемой, а для других она - лёгкий вопрос. Один и тот же текст одни дети понимают после первого чтения, другим требуется повторение, а третьим необходимы разъяснения. Говоря иначе, успешность усвоения учебного материала, темп овладения им, прочность осмысленность знаний, уровень развития ребёнка зависят не от одной только деятельности учителя, но и от познавательных возможностей и способностей учащихся, обусловленных многими факторами, в том числе особенностями восприятия, памяти, мыслительной деятельности, наконец, физическим развитием. Каждый учитель знает о наличии природных различий школьников и часто успехи или неудачи школьника объясняются именно ими. Условия среды в большинстве случаев таковы, что для многих людей не адекватны их природным задаткам. Людей, родившихся с выдающимися наследственными потенциями, намного больше, чем тех, которым эти потенции удалось реализовать. Основная и очень ответственная задача школы - раскрыть индивидуальность ребенка, помочь ей проявиться, развиться, устояться, обрести избирательность и устойчивость к социальным воздействиям. Раскрытие индивидуальности каждого ребенка в процессе обучения обеспечивает построение личностно-ориентированного образования в современной школе. 2. Цели и задачи личностно ориентированного обучения Цель: создание системы психолого-педагогических условий, позволяющих в едином классном коллективе работать с ориентацией не на "усредненного" ученика, а с каждым в отдельности с учетом индивидуальных познавательных возможностей, потребностей и интересов. Технология личностно ориентированного обучения математике обусловлена следующими задачами:
Такая дидактическая система изучается и внедряется мною с 2004 года. Я постаралась систематизировать уже накопленные сведения о данном подходе и на этой основе расширить границы его использования. Реализация личностно-ориентированного подхода является одним из методических приёмов повышения познавательной активности обучающихся и качества обучения математике. Данное представление о сущности личностно ориентированного подхода позволяет мне более целенаправленно и эффективно моделировать и строить конкретные учебные занятия, более результативно обеспечивать и поддерживать процессы самосовершенствования личности ребенка, развивая его индивидуальность. В трактовке личностно ориентированного образования наиболее концентрированно выражена мысль о том, что оно должно предстать в образовательной системе как средство дифференциации и индивидуализации обучения. 3. Система работы учителя математики состоит из следующих компонентов:
Принцип целеполагания и мотивации. Важное значение на уроке в реализации данного принципа приобретают организация и управление деятельностью учащихся по целеполаганию, мотивации и определению темы занятия, которое реализуется на практике различными путями:
Принцип открытости, понимаемый как возможность дополнять, видоизменять информацию, формы организации учебно-познавательной деятельности, реализуется на основе обработки результатов диагностики с мониторинговым подходом. Контрольная диагностика позволяет учителю объективно определять количество учеников, работающих на разных уровнях, корректировать педагогические воздействия. На занятиях главный акцент делается на самостоятельную работу с индивидуальным темпом в сочетании с приемами взаимообучения и взаимопроверки. Принцип вариативности реализуется путем использования на уроках нескольких альтернативных учебников, справочников, таблиц, что позволяет рассмотреть многие вопросы с различных позиций и выработать свой подход к их решению. Принцип направленности обучения на развитие личности ученика осуществляется через создание условий для каждого школьника по формированию индивидуального стиля деятельности, а именно через самостоятельную и контрольную работы с разноуровневыми заданиями; выбор ролей в деятельности групп; возможность выбора уровня домашнего задания. Принцип успешности обучения означает собственный успех каждого школьника, использование стимулирующего поощрения его активной деятельности при работе оценочной системы (поощрение с помощью накопления баллов, жетонов). Это позволяет увеличить интенсивность урока за счет повышения активности учащихся и возможности оценить каждого, создает высокий эмоциональный подъем и настрой на весь урок, условие для повышения интереса к предмету, увеличения количества учеников, вовлекаемых в активную учебно-познавательную деятельность. Принцип индивидуализации обучения опирается на составление индивидуальных программ по усвоению учебного материала для каждого ученика на основе результатов мониторинга по определению зоны ближайшего развития. 7. Структура личностно ориентированного урока   8. Этапы личностно ориентированного урока К уроку как основной форме организации учебного процесса в условиях личностно ориентированного обучения предъявляется ряд требований, которым я стараюсь следовать. Этап целеполагания Основная цель уроков данной педагогической технологии –повышение результативности урока через использование личностно ориентированного подхода в обучении и структуирования урока в соответствии с требованиями современности, тем самым создавая условия для проявления познавательной активности учеников. Каковы средства достижения этой цели? Прежде всего, осуществляю комплексное планирование и реализацию задач развития, образования и воспитания на основе продумывания триединой задачи урока:
Определяется место урока в системе уроков, сообщается не только тема, но и предполагаемый порядок организации учебной деятельности, совместно с учениками выбираются пути, способы и примеры решения учебных задач. При этом необходимо создать условия, обеспечивающие ученику позицию субъекта при постановке учебных задач, в ходе их реализации. На уроках должна быть создана атмосфера доброжелательности, сотрудничества, заинтересованности каждого ученика в работе класса, положительного эмоционального настроя на работу в течение всего урока. Поведение учителя на уроке – это умение владеть классом. Учитель должен организовать работу каждого школьника, создавая рабочий настрой, искреннее общение и деловой контакт. Все это повышает интерес, внимание, активность. Такое поведение учителя позволяет отдельным ученикам с учетом их индивидуальных способностей как-то положительно проявить себя, а стиль и тон учителя поможет им в этом. На уроках необходимо сочетание различных форм коллективной и индивидуальной работы, организуется самостоятельная работа учащихся, сокращаются однотипные упражнения. Создаются на уроках ситуации активного общения, не только монолога, но и диалога, полилога, позволяющих ученику выразить себя, проявить инициативу, самостоятельность в способах выбора познавательной деятельности, типов заданий, вида и форм учебного материала. Этап актуализации субъектного опыта Ключевым понятием личностно ориентированного обучения является Субъективный опыт учащихся, поэтому этап актуализации знаний связан с систематизацией и обобщением изученного, на этом этапе учитывается учебный математический опыт учащихся. Так, обобщению и систематизации сведений об углах перед изучением смежных углов способствуют вопросы: 1) что уже знаем об углах ( важно, чтобы учащиеся перечислили: определение, элементы, способы обозначения, виды углов, свойства измерения углов), 2) что учились делать с углами (строить различные виды углов, обозначать углы разными способами, находить величину угла с помощью транспортира). При личностно ориентированном обучении учитель старается предоставить учащимся возможность проявить инициативу, мотивирует любой вид деятельности. Поэтому этап актуализации знаний перед изучением смежных углов может быть следующим образом: У  читель: На этом уроке мы с вами продолжим знакомство с геометрическими фигурами. Но в начале повторим то, что нам известно. На доске изображен рисунок. Какие геометрические вопросы вы могли бы задать, глядя на этот рисунок? читель: На этом уроке мы с вами продолжим знакомство с геометрическими фигурами. Но в начале повторим то, что нам известно. На доске изображен рисунок. Какие геометрические вопросы вы могли бы задать, глядя на этот рисунок?  С А Д О В  Е Учащиеся могут задать следующие вопросы:
Данный этап может сопровождается устной работой. Для этого использую, такие задания. Пример: “На доске прикреплены карточки с примерами и результаты этих примеров. Но результаты почему-то оказались перепутанными. По выбору кто, какой пример хочет, выбирает и находит к нему результат”. Пример: “Найди ошибку”. На доске записаны равенства, примерно 10. Ученику предлагается отыскать ошибку в решении (ответе) одного или нескольких заданий. Пример: Игра “Интеллектуальный марафон”. Учащимся предлагается найти произведение всех чисел, сидящих на дереве. Данное задание можно оформить наглядно, что вносит свою изюминку. Такие задания развивают воображение, внимание, память, мышление. Все задания содержат в себе элементы необычного, удивительного, вызывают интерес у школьников к предмету и способствуют положительной эмоциональной обстановке учения. Основу таких заданий составляют задания, связанные с программным материалом и способствующие усвоению и закреплению его учащимися. Для проведения устного счёта стала привлекать самих детей. Самое “ценное” для меня то, что ребята сами составляют задания по теме для устного счёта. И на уроке “автор” сам проводит устный счёт. Этап изучения нового материала При личностно ориентированном обучении основными образовательными источниками являются учебный предмет и процесс его освоения, поэтому изучение нового материала строится с опорой на учебный опыт учащихся, что обеспечивает их успешность при осуществлении поисковой или исследовательской деятельности. При изучении нового материала стараюсь “заразить” ребят поиском решения той или иной проблемы. Опыт работы показывает, что глубокие, прочные и, главное, осознанные знания могут получить все школьники, если развивать у них не столько память, сколько логическое мышление. Важным и значимым становятся математические сведения, если они затрагивают личность, если с ними связаны жизненный и личный опыт. При этом учебная ситуация преобразуется в личностно-значимую, а учебная информация – в событие самого ученика. Задачи решаются и воспринимаются детьми совсем иначе, если в их условие входят понятия напрямую связанные с окружающей действительностью. Данные для условия задач ученики собирают сами. Например, иллюстрирующий возможность сделать учебный материал ярким и запоминающимся, - из курса стереометрии. При изучении темы "Пирамиды" не обойтись без обращения к одному из "чудес света" - египетским пирамидам. Оказывается, их геометрические параметры подчинены удивительным закономерностям, которые можно использовать для составления интересных и полезных задач. Школьники гораздо более увлечённо вычисляют углы наклона боковых ребер и боковых граней к плоскости основания грандиозного сооружения, построенного в третьем тысячелетии до нашей эры, чем абстрактной пирамиды из типовой задачки. Этап применения знаний Закрепление изученного материала практически всегда сопровождаю заданиями на составление обратной задачи. Такая форма работы применима к любой теме курса математики. Если учащиеся способны составлять обратную задачу, значит, они понимают смысл данного задания, видят взаимосвязь компонент. Другой вариант: Использую группу карточек, позволяющую ученику самостоятельно выбирать тип, вид, форму материала пользоваться индивидуальным способом учебной работы, в которую входят задания трёх различных уровней сложности. К I - задания, соответствующие обязательным результатам обучения. Ко II – задания, на умение применять знания в ситуациях сходных, с теми, что были разобраны в классе. К III – задания, для школьников, проявляющих повышенный интерес к математике. Пред началом выполнения, чётко поясняю каждое из предложенных на выбор учебных заданий, показываю значимость его выполнения, раскрываю критерии оценивания каждой карточки. Уместно предложить выполнить самостоятельную работу по одному из предложенных вариантов: а) полностью самостоятельно; б) по аналогии с решениями упражнений, записанных на доске; в) с использованием учебника. Этап проверки знаний На данном этапе использую различные тестовые задания. Использую тестовые задания как и на бумажном носителе, так и на электронном. Ученикам предоставляется выбор, с помощью какого источника им удобней выполнить задание. Предлагаю набор тестов, состоящий из трёх видов заданий, различающихся по форме и способу предъявления их учащимся:
Таким образом, предлагаемые тесты ставят ребёнка в ситуацию выбора такого задания, с которым ребёнок обязательно справится, т.е. удовлетворение потребности в самовыражении, самореализации, что обеспечит успех. Личностно-ориентированный подход предполагает привлечение к оцениванию самих учащихся. Для этого, после выполнения тестов учащимся предлагается оценить себя. На доске написаны ключи к заданиям, он проверяет их и оценивает. Если вдруг по каким-то причинам ребёнок поставил неудовлетворительную оценку, то в журнал не выставляю, а оставляет за ним право еще раз подготовиться и выполнить тест. Как уже говорила выше, наряду с тестами на бумаге использую тестовые задания с применением компьютера. Применение компьютера дает возможность сделать процесс обучения более активным, придать ему характер исследования и поиска. Такая установка даёт возможность каждому ученику работать самостоятельно, не отвлекать соседа, спрашивая ответ на тот или иной вопрос, так как подача вопросов и ответ идёт у всех по-разному. Целесообразно использовать различные виды тестов и формы представления заданий. В этом случае, во-первых, процесс тестирования становится менее утомительным, что повышает интерес учащихся к выполнению заданий, а во-вторых, нет опасности, что тестирование превратится в выявление навыка отвечать на задания только данного типа. При проверке знаний учащихся, кроме перечисленных выше методов, выясняю степень усвоения материала учащимися с помощью листов взаимоконтроля, которые содержат перечень программных вопросов по изучаемой теме. Ученики отвечают на вопросы друг другу по очереди и взаимно оценивают друг друга. Контроль учебной деятельности должен быть направлен на выявление динамики приобретения знаний, развития умений и навыков. Для отслеживания этой динамики используются различные виды контроля:
Очень важной является процедура оценивания, которая также должна быть направлена на раскрытие потенциальных возможностей учащихся с учётом их индивидуальных достижений. На этапе изучения нового материала, выполнения тренировочных упражнений, в процессе поисковой работы оценивать учащихся некорректно и допустимо только в случае значительных достижений. В основном ведётся лишь наблюдение за ходом работы, за тем, как относится школьник к учению, какова его познавательная активность. Если ученик не справился с заданием, необходимо выяснить причины, организовать необходимую коррекционную работу по ликвидации пробелов в знаниях и умениях. Затем предложить выполнить задание, аналогичное тому, с которым он не справился. При составлении проверочных, самостоятельных и итоговых работ не ограничиваюсь заданиями репродуктивного уровня, которые должны входить в работу для того, чтобы ученики увидели степень своего продвижения в учёбе и определили зону своего ближайшего развития в материале учебного предмета. Этап “Домашнее задание” Любой урок, как правило, начинаю с взаимоконтроля домашнего задания. Один или двое учащихся (по очереди) записывают своё выполнение домашнего задания на доске (на перемене). Остальные учащиеся обмениваются тетрадями и проверяют выполнение задания соседом, находят и исправляют ошибки, дают друг другу консультации по возникшей при проверке проблеме, высказывают свои мнения по вопросу выполнения задания соседом, кратко комментируют допущенные ошибки, обсуждают выполнение задания учащимися у доски, предлагают другой способ решения. Если задание несложное, то проверяем устно. Я во время взаимопроверки домашнего задания обхожу класс, поощряю словом, оказываю помощь в случае необходимости, слушаю ответы учащихся и даю свои комментарии к их ответам. Здесь очень важно увидеть, заметить, поощрить, кто и как выполнил домашнее задание, потому что оно же задаётся на выбор. Такая форма работы позволяет максимально проконтролировать уровень усвоения изученного материала, выявить те этапы работы, которые вызывают затруднения в выполнении задания, ответить на вопрос каждого ученика При задании на дом указывается не только тема, но и объём заданий, которые часто носят дифференцированный характер и ученику, как и в ходе урока, предоставляется право выбора уровня, вида и формы изучения учебного материала. Этап «Рефлексия» Итоговым этапом урока является рефлексия. Высказывается каждый ученик, и уже с учётом сказанного планирую следующие уроки, ведущие к новым знаниям. Можно предложить продолжить фразу: «Сегодня на уроке я узнал…» «Сегодня на уроке я научился…» «Сегодня на уроке мне понравилось…» «Сегодня на уроке мне не понравилось…» «Сегодня на уроке мне не удалось…». В диалоге с учащимися не просто повторяются формулировки нового материала, а систематизируется весь изученный к этому моменту материал и ситуации его применения. Для этого удобно задавать вопросы типа: “С каким новым понятием (свойством, утверждением, видом задач) познакомились? Что об этом надо знать?”, “Что можно рассказать о ситуациях применения нового (трудностях, с которыми встретились, возможных ошибках и способах их предотвращения)?”, “Чему учились на уроке? Что помогало при этом? Обсуждение с детьми в конце урока не только того, что нового узнали, но и того, что понравилось (не понравилось) и почему, что бы хотелось выполнить ещё раз, а что сделать по-другому. 9. Примеры методов и приемов, применяемых на личностно ориентированном уроке математики 9.1 Речевые обороты, которые используются для создания ситуации успеха на уроке
9.2 Использование исторического материала Привлекая исторический материал, материал из смежных дисциплин, подчеркивая красоту и мощь математики, повышается интерес к предмету.
История происхождения некоторых терминов Деление, делимое, делитель. От франц. Dividere- делить, распределять. Квадрат. Термин quadratus означает - четырехугольный и получился как буквальный перевод соответствующего греческого названия. Куб. Термин происходит от греческого - игральная кость. Так как она имела форму кубика, то название перешло на любое тело той же формы. Название введено пифагорейцами. Математика. Это слово греческого - наука, происхождения: в свою очередь произошло от соответствующего глагола, означавшего учусь через размышление. Пифагорейцы знали четыре раздела математики: учение о числах (арифметику), теорию музыки (гармонию), учение о фигурах (геометрию), астрономию и астрологию. Минус. Термин образован от латинского minus – меньше. Плюс. Термин произошел от слова plus? ?больше. Произведение. Среди многочисленных обозначений умножения употреблялся и прямоугольник как символ того, что площадь его получается при перемножении двух измерений. В связи с этим вплоть до XVII в. вместо произведение говорили – прямоугольник. Точка. Слово происходит от глагола ткнуть и означает результат мгновенного прикосновения, укола. Тот же смысл имеет и латинское. punctum, от которого произошло русское слово пункт.
Использование исторических сюжетов Урок алгебры в 9 классе. Тема : «Сумма n – первых членов геометрической прогрессии». Легенда о шахматной доске Шахматы – одна из самых древних игр. Она существует уже многие века и неудивительно, что с нею связаны придания. Шахматная игра была придумана в Индии, и когда индусский царь Шерам познакомился с нею, он был восхищен ее остроумием и разнообразием возможных в ней положений. Узнав, что она изобретена одним из его подданных, царь приказал его позвать, чтобы лично наградить за удачную выдумку. Изобретатель, его звали Сета, явился к трону повелителя. Это был скромно одетый ученый, получавший средства к жизни от своих учеников. - Я желаю достойно вознаградить тебя, Сета, за прекрасную игру, которую ты придумал, - сказал царь – я достаточно богат, чтобы исполнить самое смелое твое пожелание – предложил царь. - Назови награду, которая тебя удовлетворит, и ты получишь ее. Сета молчал. - Не робей, - ободрил его царь – выскажи свое мнение. Я не пожалею ничего, чтобы исполнить его. На что Сета сказал, что он обдумает ответ и завтра сообщит царю свою просьбу. На другой день, когда Сета сообщил свою просьбу, царь удивился беспримерной скромности бедного мудреца. - Повелитель, - сказал Сета, - прикажи выдать мне за первую клетку шахматной доски одно пшеничное зерно. За вторую клетку выдать 2 зерна, за третью – 4, за четвертую – 8, за пятую – 16, за шестую – 32… - Довольно, - с раздражением прервал его царь. – Ты получишь свои зерна за все 64 клетки доски, согласно твоему желанию. Но знай, что твоя просьба недостойна моей щедрости. Поистине, как учитель, ты мог бы показать лучший пример уважения к доброте своего государя. Слуги мои вынесут тебе твой мешок с пшеницей. Царь Шерам засмеялся. Учитель: Ребята, как вы думаете, стоит ли царю смеяться? Задача 1, 2, 4, 8, 16, 32, … = ? Учитель: Как велико это число? Кто может объяснить? Ученик: Если бы царю удалось засеять пшеницей площадь всей поверхности Земли, считая моря, и океаны, и горы, и пустыни и получить хороший урожай, то лет за пять он смог бы рассчитаться. Это «чудовищное» число звучит так: 18 квинтиллионов 446 квадриллионов 744 триллиона 73 миллиарда 709 миллионов 551 тысяча 615. И все-таки , история о шахматной доске могла бы закончиться иначе, будь царь силен в математике. Для этого нужно было лишь предложить изобретателю самому отсчитать себе зерно за зерном всю причитавшуюся ему пшеницу, на это потребовалось бы 586 549 402 017 лет. 9.3 Внесение занимательных заданий, выходящих «за страницы учебника» Игра объединяет класс: открываются умение подстраховать друг друга, выслушать каждое мнение. Здесь важны не столько знания, сколько умения детей обсуждать вопрос и выслушать позицию другого. У ребят меняются мнения о своих одноклассниках, при этом меняется и их статус в группе. 5 класс. Тема: «Необычное сложение"Цели:
Оборудование: на доске портрет Карла Фридриха Гаусса, годы его жизни.  I. Актуализация знаний 1. Найдите закономерность В приведенной ниже таблице числа расположены в соответствии с определенной закономерностью. Установите эту закономерность и назовите число, которое следовало бы вписать в пустое место таблицы:
Ответ: 10. 2. Посмотрите на число и запомните: 26 101 418 2226. Число убирается. Учащиеся должны по памяти воспроизвести число. Так как, число большое, то должны увидеть какую-то закономерность. Ответ: Закономерность состоит в следующем: 2 6 10 14 18 22 26. Достаточно запомнить первое число, и к нему последовательно прибавлять число 4 II. Проверка домашнего задания Числовой ребус: 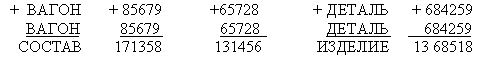 III. Вводное слово учителя Истории математики известны случаи очень раннего проявления математических способностей. Французский ученый Блез Паскаль стал интересоваться математикой в столь раннем возрасте, что отец ему запретил ею заниматься. Однако, зайдя через некоторое время в детскую комнату, он обнаружил. Что мальчик углубился в рассмотрение какого-то рисунка из прямых линий и окружностей. Очень рано раскрылись дарования и у Карла Гаусса, позднее ставшего одним из крупнейших математиков X IX века (его даже называли “царем математики”). Рассказывают, что в возрасте трех лет он заметил ошибку, сделанную его отцом в расчетах. А семи лет мальчик пошел в школу. В то время в одной классной комнате занимались ученики разных классов. Чтобы занять первоклассников, пока он будет заниматься с третьим классом, учитель велел им сложить все числа от 1 до 100. Но не успел он закончить чтение условия задачи, как маленький Карл написал на своей грифельной доске ответ и положил на учительский стол. С сожалением смотрел преподаватель на мальчика: ясно было, что за такой короткий срок он не мог сделать столько сложений. Остальные ученики терпеливо складывали. Когда учитель закончил занятия с третьеклассниками, он взял со своего стола грифельные доски. Ни у кого не было правильного результата. И только на доске Карла стоял ответ: 5050, причем никаких вычислений не было. – Как же ты сосчитал? – спросил учитель. – Очень просто, – ответил мальчик. Как же вычислил маленький Гаусс? – На этот вопрос нам и нужно сегодня ответить. И вычислить сумму так же быстро, как это сделал Гаусс. Математический факт IV. Решение задач Задача 1. Найдите сумму всех чисел от 1 до 10. Учащиеся решают самостоятельно. 45 + 10 = 55. 2-ой вариант решения: + 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 10 + 9 + 8 + 7 + 6 + 5 + 4 + 3 + 2 + 1 11 + 11 + 11 + 11 + 11 + 11 + 11+ 11 + 11 + 11 Итак, получилось 10 пар, по 11, но так как числа брали 2 раза, то надо 10 : 2 = 5. Значит 11· 5 = 55. Задача 2. Найдите сумму всех чисел от 1 до 20. Решение: Можно составить пары из чисел: 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + ... + 20 = (1 + 20) + (2 + 19) + (3 + 18) + (4 + 17) + (5 + 16) + (6 + 17 ) + (7 + 16) + ( 8 + 13) + (9 + 12) + (10 + 1) = 21 • 10 = 210 Задача 3. Итак, собственно задача о нахождении суммы чисел от 1 до 100. Решение: + 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + ... + 100 100 + 99 + 98 + 97 + 96 + 95 + 94 + 93 + 92 + 91 + … + 1 101+ 101 + 101 + 101 + 101 + 101 + 101+ 101 + 101 +101 + ... + 101 В каждой сумме получилось по 110, но т.к. чисел всего 100, а брали их по два раза, значит их надо разделить на 2. 101 · (100 : 2) = 5050 Задача 4. Найти сумму: 20 + 40 + 60 + … + 460 + 480 + 500. Алгоритм: 1. Найдем сколько всего чисел в этой последовательности. Так как, здесь записана сумма чисел, которые делятся на 20, начиная с 20 до 500. Поэтому найдем их количество: 20 n = 500, n = 25. Всего 25 пар. 2. Найдем сумму первого и последнего числа: 20 + 500 = 520. 3. Вычислим непосредственно сумму по формуле: Сумма чисел = (сумма (первого и последнего числа) · количество пар) : 2 (520 · 25) : 2 = 4160 Задача 5. Найти сумму: 30 + 60 + 90 + … + 540 + 570 + 600. Решение: 1. 30 n = 600, n = 20 2. 30 + 600 = 630 3. 630 · (20 : 2) = 6300 Задача 6. Найти сумму: 6 + 12 + 18 + … + 90 + 96. Решение: 1. 6 n = 96, n = 16 2. 6 + 96 = 102 3. 102 · (16 : 2) = 816 Задача 7. Найти сумму: 100 + 200 + 300 + … + 900 + 1000. Решение: 1. 100 n = 1000, n = 10 2. 100 + 1000= 1100 3. 1100 · (10 : 2) = 5500 Задача 8. Найти сумму: 150 + 250 + 350 + … + 950. Решение: (150 + 950) + ( 250 + 850) + (350 + 750 ) + (450 + 650) + 550 = 1100 · 4 + 550 = 4950 1. 50 n = 950, n = 19. Но так как здесь сумма начинается не с 50, и не со 100, а со 150. Значит нужно исключить числа 50, 100, 200, 300, 400, 500, 600, 700, 800, 900. Их всего 10. 19 –10 = 9 2. 150 + 950 = 1100 3. 1100 · 9 : 2 = 4950 V. Итог урока VI. Дополнительные задачи 1. Какой цифрой оканчивается сумма всех трехзначных чисел? Решение: 100 + 101 + 102 + … + 998 + 999 = (101 + 999) + (102 + 998) + … + (549 + 551) + (100 + 550). Каждая сумма в скобках оканчивается нулем. Поэтому сумма всех трехзначных чисел тоже оканчивается нулем. 2. Вычислите сумму всех нечетных чисел, находящихся в первой тысяче. Решение: 1 + 2 + 3 + … + 997 + 999 = (1 + 999) + ( 3 + 997) + (5 + 995) + … + (499 + 501) = 1000 · 250 = 250000. Всего чисел от 1 до 1000 – 1000 (тысяча), нечетных и четных наполовину. Значит нечетных чисел в первой тысяче 500. Пар слагаемых заключенных в скобки – 250. 3. Вычислите наиболее удобным способом: 99 – 97 + 95 – 93 +…+ 3 – 1 Решение: Нечетных чисел в первой сотне 50. Всего пар слагаемых 25, значит (99 – 97) + (95 – 93) + … + (3 – 1) = 2 · 25 = 50 4. Вычислите наиболее удобным способом: 101 – 99 + 97 – 95 + 93 –… 5– 3 +1 Решение: Нечетных чисел в первой сотне 50, но добавилось число 101, значит 51 нечетное число, но 1 не образовала пары, значит пар будет 25, и 1 отдельно (101 – 99 ) + (97 – 95) + (93 – 91) + … + (5 – 3) + 1 = 2 · 25 + 1 = 51. 5. Вычислите сумму: 1 + 1 + 2 + 3 + 5 +…+ 144 = ? Решение: Сначала нужно найти закономерность. Каждое следующее число равно сумме двух предыдущих. Например: 1 + 1 = 2, 1 + 2 = 3, 3 + 5 = 8 и т. д. Получаем следующую сумму: 1 + 1 + 2 + 3 + 5 + 8 + 13 + 21 + 34 + 55 + 89 + 144 = 377 9.4 Связь абстракции с действительностью Число не является основанием особо важной и наиболее часто встечающейся показательной функции, которая называется экспонентой: f(x)=ех=ехр(х). (Exponent в переводе с немецкого означает показатель. Сам термин exponenten возник при не совсем точном переводе с греческого слова, которым Диофант обозначал квадрат неизвестной величины.) Экспоненциальному закону подчинены многие зависимости в живой и неживой природе. Гибкая цепь провисает по кривой, которая так и называется - цепная линия. Так же выгибается парус, надутый ветром.   Сечение вулканов вертикальной плоскостью имеет форму цепной линии. Вездесущее число е начертано даже на паутине. Французский энтомолог Жан Анри Фарб в книге "Жизнь паука" писал: "Рассмотрим внимательно сплетённую за ночь паутину. Усеянные крохотными капельками, её липкие нити провисают под тяжестью груза, образуя цепные линии, и вся сеть становится похожей на множество ожерелий, как бы повторяющих очертания невидимого колокола. Стоит лишь лучу солнца проникнуть сквозь туман, как паутина начинает переливаться всеми цветами радуги, и число е предстаёт перед нами во всём своём великолепии". 10.Результативность использования личностно ориентированного обучения
11. Заключение Личностно ориентированный подход в обучении – это важнейший принцип воспитания и обучения. Он означает действенное внимание к каждому ученику, его творческой индивидуальности в условиях классно- урочной системы обучение по обязательным учебным программам, предполагает сочетание фронтальных, групповых и индивидуальных заданий для повышение качества и развития каждого ученика. Успешно развивается познавательная активность, интеллектуальная деятельность каждого ученика с учётом его возможностей и способностей. Технология личностно ориентированного обучения математике вовлекает каждого ученика в процесс само- и соуправления своим развитием. 12. Литература
|