Разработка урока по теме: «Производная функции»
 Скачать 58.36 Kb. Скачать 58.36 Kb.
|
| ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ГОРОДА МОСКВЫ СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА №136 Разработка урока по теме: «Производная функции» Урок подготовила учитель математики ГБОУ СОШ № 136 Груздева Светлана Ивановна 2012 г. Конспект урока. Тема: «Производная функции». Цели: систематизация знаний и способов действий. Задачи: образовательные: совершенствовать технику дифференцирования; создавать условия для воспроизведения в памяти учащихся системы опорных знаний и умений; развивающие: развививать умение наблюдать, классифицировать, анализировать математические ситуации, повышать вычислительную культуру учащихся, развивать математическую речь, развивать коммуникативную способность учащихся; воспитательные: воспитывать такие качества личности, как познавательную активность, самостоятельность, упорство в достижении цели. Оборудование: мультимедийный проектор, слайды, созданные в программе Microsoft Power Point, компьютеры, программный продукт «Математика для всех» (web –приложение) с тестовыми заданиями (или использовать любой набор тестовых заданий по теме «Производная функции»), контрольные оценочные листы, тексты заданий для экспертов. Структура урока:
оценочных листах с последующей проверкой экспертами) (10 мин)
Ход урока.
Проверяется подготовленность классного помещения и готовность учащихся к уроку.
На экране появляется слайд: «Производная функции». Сегодня мы проводим повторительно – обобщающий урок по теме «Производная функции». В ходе урока нам предстоит выяснить:
Учитель напоминает, что эту тему необходимо знать каждому очень хорошо, чтобы в дальнейшем научиться проводить исследование функций с помощью производных и строить графики различных функций. Это основное применение производной.
Начинаем работу с повторения теории.
На экране появляется слайд «Правила вычисления производных». 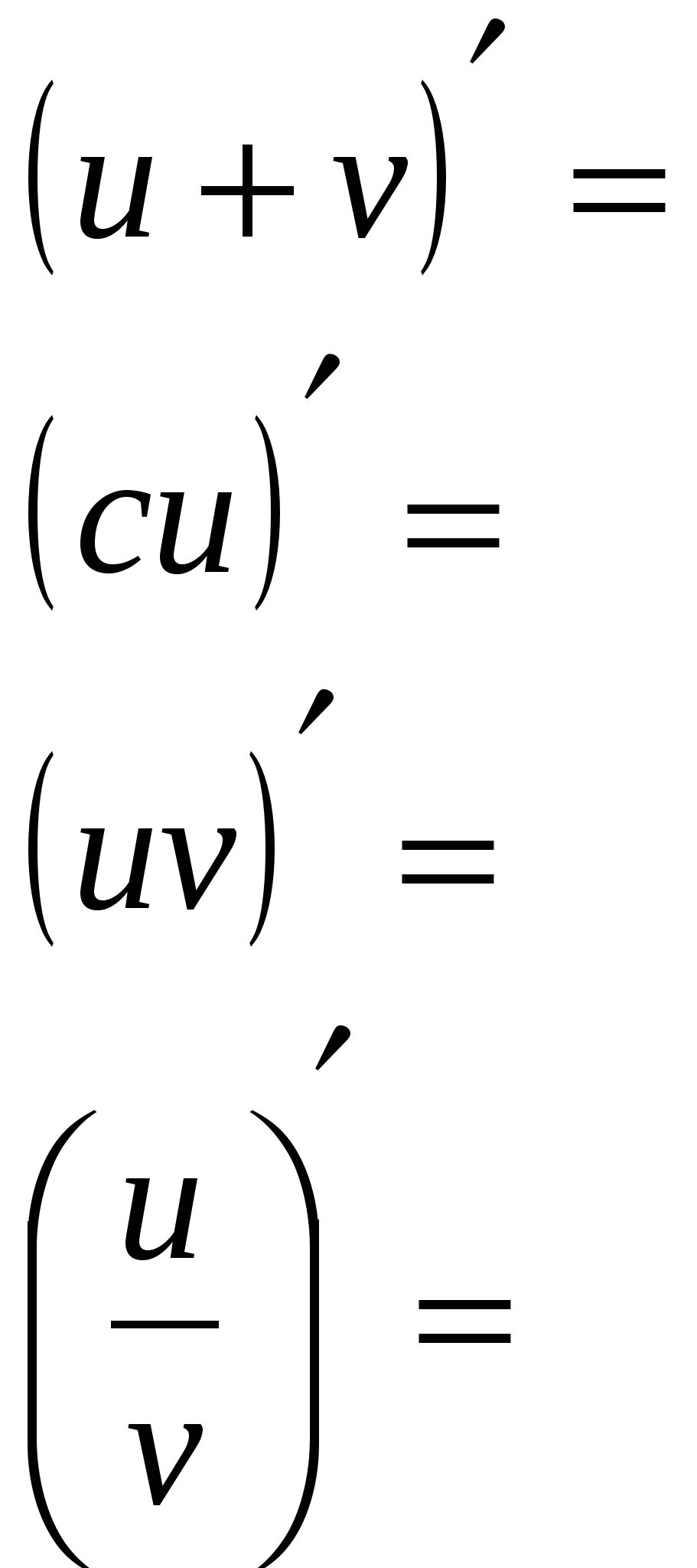 Учащиеся проговаривают каждое правило. Учитель акцентирует внимание учащихся на грамотности математической речи.
На экране появляется слайд «Таблица производных функций».  Учащиеся фронтально повторяют таблицу производных элементарных функций. Затем на экране появляется слайд «Производная сложной функции». Учитель напоминает учащимся определение сложной функции и просит сформулировать правило нахождения производной сложной функции. Делает акцент на то, что при нахождении производной сложной функции нужно не забывать находить производную внутренней функции. Учитель напоминает, что на уроке каждый ученик пройдет тестирование по теме «Производная функции» на компьютере. Первыми начнут эту работу эксперты, которые назначаются учителем среди учащихся. Команда экспертов включает компьютер, вводят свой логин и пароль, выбирают тему «Производная» и приступают к тестированию.
На экране появляется слайд «Устные упражнения». Учащиеся применяют теорию на практике. Выполняя устные упражнения, учащиеся комментируют, что применяли при вычислениях. Учитель обращает внимание на речь учащихся. Задание Найдите производные функции:  Учитель подводит итог разминке, акцентируя внимание учащихся на правильность вычисления производной сложной функции и необходимости иногда преобразовать функцию, прежде чем вычислять производную.
На экране появляется слайд «Порешаем?...». Работа немного усложняется. Учащимся предлагается задание: найдите значение производной функции в данной точке. Учащиеся выполняют задание самостоятельно. Учитель, проходя между рядами, наблюдает за деятельностью учащихся и при необходимости корректирует их. Проверка осуществляется устно. Задание проверяется на экране. Решение. Ответ: 0.
Работа проходит у доски. Предлагается задание: найдите те значения аргумента, при котором значение производной равно нулю. Учащиеся выполняют задания с комментариями. Задание 1 Решите уравнение Решение. 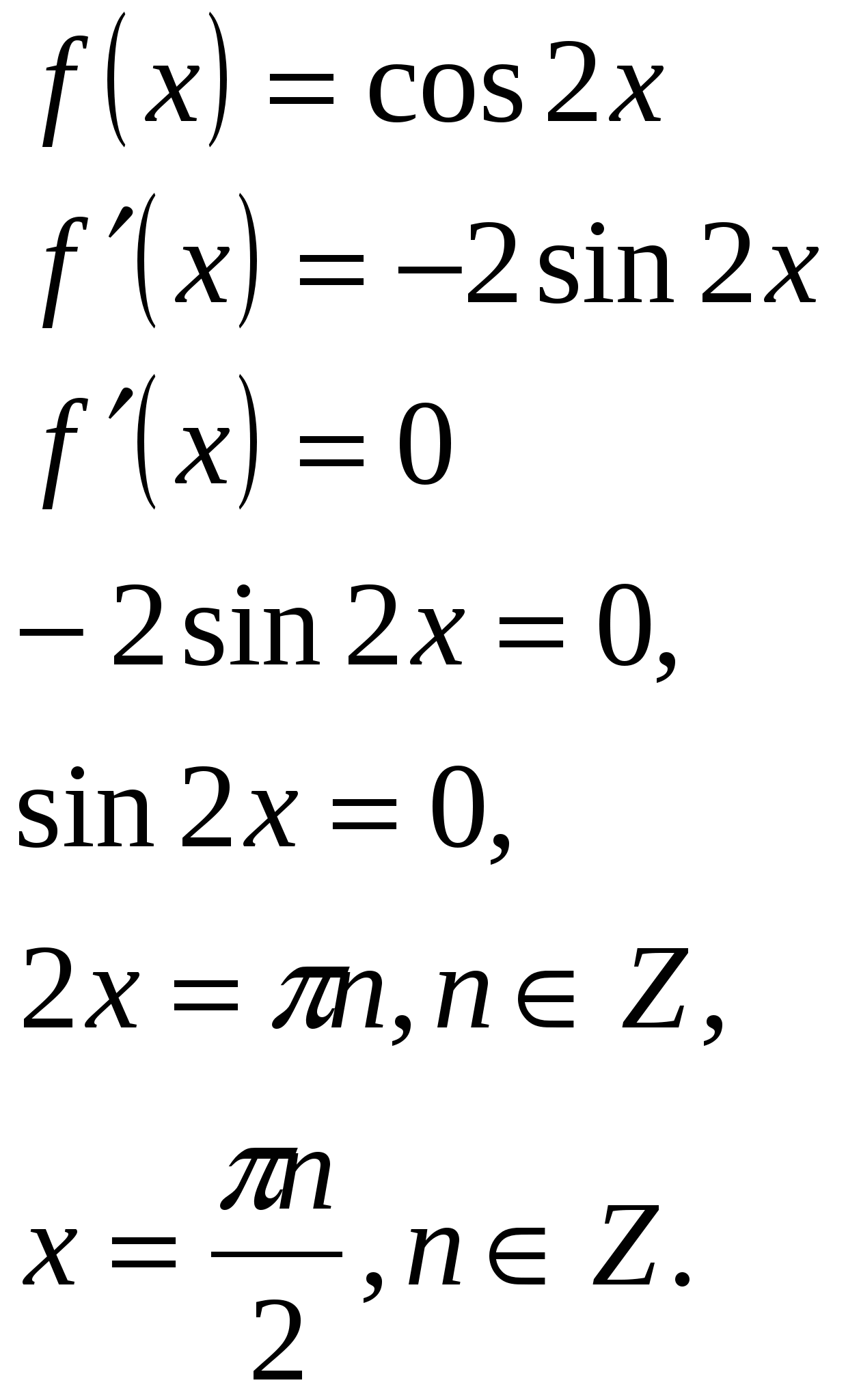 Ответ: Задание 2. Решите уравнение Решение.  Ответ:
Очень важно уметь не только правильно выполнять задание, но и находить ошибки. Учащимся предлагается задание: посмотреть на решение и, если смогут найти ошибку, указать ее. На экране появляется слайд «Найдите ошибку». Учащиеся, если находят ошибку, то указывают её и говорят правильное решение.
Проверка знаний по теме «Производная функции» осуществляется дифференцировано. Учитель распределяет задания. Учитель определяет сколько человек работают за компьютерами и проводит инструктаж: включить компьютер, ввести свой логин и пароль, выбрать тему «Производная функции», открыть тест. У каждого учащегося на столе лежит бланк, ученики оценивают результативность выполнения данного теста и заносят эту оценку в бланк. Работу выполняют в течение 10 минут. После окончания работы учащиеся в бланк ставят ту оценку, которую поставил компьютер. Лист сдают учителю. Эксперты получают задание повышенной сложности. Работу сдают на проверку учителю. Слабоуспевающие учащиеся получают контрольный лист с заданиями, делают самооценку предложенной работы, выполняют её. Затем эксперты её проверяют, выставляют оценку и сдают контрольный лист учителю. Работа длится 10 минут.
На экране появляется диаграмма результатов выполнения тестирования. Учитель комментирует их.
Все учащиеся класса получают задание из учебника А.Н. Колмогорова «Алгебра и начала анализа»: стр.171 № 3(3). Дополнительно: ученикам, получивших за тестирование оценку «5», выдается дополнительное задание на карточке; ученики, допустившие ошибки в тестировании, делают работу над ошибками, повторяют теорию и проходят повторное тестирование на следующем уроке.
Учитель предлагает продолжить фразу и ответить на вопрос. Продолжите фразу «Сегодня на уроке я повторил…» Вопрос: - А зачем мы учимся дифференцировать функцию? (учимся дифференцировать функцию для исследования функций с помощью производной и построения графиков функций) |