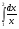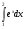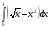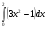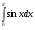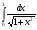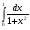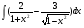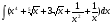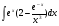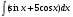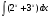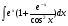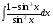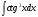Практическое занятие №3 «Исследование и построение графиков сложных функций» Задание
 Скачать 72.31 Kb. Скачать 72.31 Kb.
|
| Практическое занятие № 3 «Исследование и построение графиков сложных функций» Задание Исследовать функцию и построить её график:
Порядок проведения работы:
Оформление работы:
Методические указания по проведениюпрактической работы № 4Основные методы интегрированияЦель работы: Используя теоретический материал и образцы решения задач, решить примеры по теме «Основные методы интегрирования»» Перечень справочной литературы :
Краткие теоретические сведения: Определенный интеграл Определение. Пусть функция 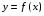 определена на отрезке [a;b], a<b. Разобьем этот отрезок на n произвольных частей точками определена на отрезке [a;b], a<b. Разобьем этот отрезок на n произвольных частей точками 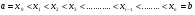 В каждом из полученных частичных отрезков 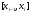 выберем произвольную точку Сi выберем произвольную точку Сi 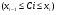 и составим сумму и составим сумму 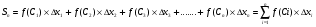 (*) (*) где 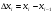 . Сумма вида (*) называется интегральной суммой для функции . Сумма вида (*) называется интегральной суммой для функции 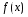 на отрезке [a;b]. на отрезке [a;b].Обозначим через 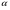 длину наибольшего частичного отрезка разбиения: длину наибольшего частичного отрезка разбиения: 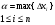 Определение. Если существует конечный предел интегральной суммы 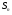 , когда , когда 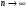 так, что так, что  , то этот предел называют определенным интегралом от функции , то этот предел называют определенным интегралом от функции 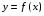 на отрезке [a;b] и обозначают следующим образом: на отрезке [a;b] и обозначают следующим образом: 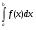 или или 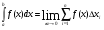 . В этом случае функция . В этом случае функция 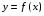 называется интегрируемой на отрезке [a;b] . Числа a и b называются соответственно нижним и верхним пределами интегрирования, называется интегрируемой на отрезке [a;b] . Числа a и b называются соответственно нижним и верхним пределами интегрирования, 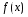 – подынтегральной функцией, – подынтегральной функцией, 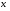 – переменной интегрирования. – переменной интегрирования.Отметим, что непрерывность функции является достаточным условием ее интегрируемости. Основные свойства определенного интеграла 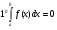 ; ; 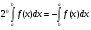 ; ; 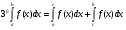 ; где a, b, c любые числа. ; где a, b, c любые числа. 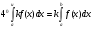 ; ; 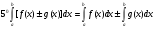 . .Формула Ньютона – Лейбница Если функция 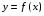 непрерывна на отрезке [a;b] и функция у = F(x) является некоторой ее первообразной на этом отрезке, то имеет место формула Ньютона – Лейбница непрерывна на отрезке [a;b] и функция у = F(x) является некоторой ее первообразной на этом отрезке, то имеет место формула Ньютона – Лейбница 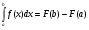 . .Вычисление определенных интегралов Простым и удобным методом вычисления определенного интеграла 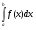 от непрерывной функции является формула Ньютона-Лейбница: от непрерывной функции является формула Ньютона-Лейбница: 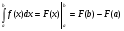 . .При вычислении определенных интегралов широко используется метод замены переменной и метод интегрирования по частям. Интегрирование подстановкой Пусть для вычисления интеграла 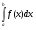 от непрерывной функции сделана подстановка от непрерывной функции сделана подстановка 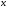 = =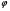 (t) (t) Теорема. Если: 1) функция 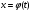 и её производная и её производная 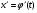 непрерывны при непрерывны при 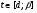 ; ; 2) множеством значений функции 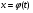 при при 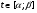 является отрезок [a;b]; является отрезок [a;b];3) 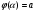 и и 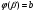 то то 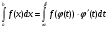 Интегрирование по частям Теорема. Если функции 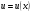  и и 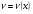 имеют непрерывные производные на отрезке [a;b], то имеет место формула имеют непрерывные производные на отрезке [a;b], то имеет место формула 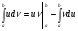 . .Пример. Вычислить 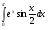 . .Решение: 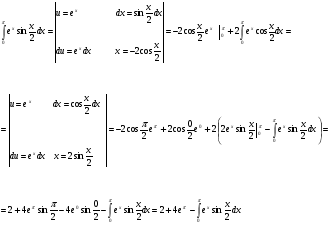 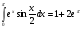 Ответ: 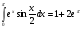 Неопределенный интеграл Основные свойства неопределенного интеграла 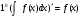 ; ; 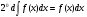 ; ;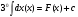 ; ; 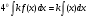 ; ;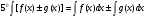 . .12.2. Таблица основных интегралов. 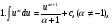 в частности, в частности, 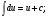 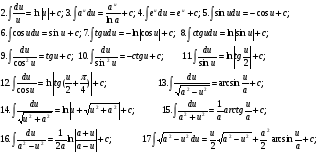 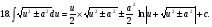 Основные методы интегрирования Метод непосредственного интегрирования Определение. Метод интегрирования, при котором данный интеграл путем тождественных преобразований подынтегральной функции (или выражения) и применения свойств неопределенного интегрирования приводится к одному или нескольким табличным интегралом, называется непосредственном интегрированием. Примеры: 1) 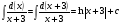 2) 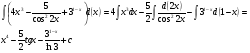 Метод интегрирования подстановкой Метод подстановки (или замены переменной) заключается в том, что заменяют 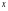 на на 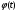 , где , где 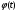 - непрерывно дифференцируемая функция, полагают - непрерывно дифференцируемая функция, полагают 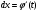 и получают и получают 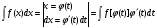 . .Примеры: 1) 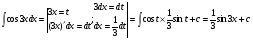 2) 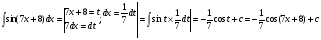 3) 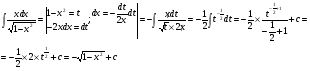 4) 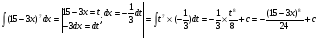 13.3. Метод интегрирования по частям 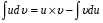
Примеры: 1) 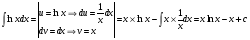 2) 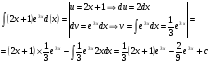 Порядок проведения работы:
Оформление работы: № 1Вычислить определенный интегралы:
№2. Применяя метод непосредственного интегрирования, вычислить интегралы:
№3. Пользуясь методом подстановки вычислить интегралы: Вариант 1 Вариант 2 1. 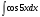 1. 1. 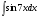 2. 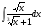 2. 2. 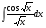 3. 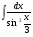 3. 3. 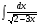 4. 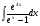 4. 4. 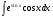 №4. С помощью метода интегрирования по частям вычислить интегралы: Вариант 1 Вариант 2 1. 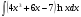 1. 1. 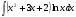 2. 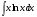 2. 2. 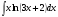 3. 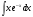 3. 3. 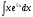 4. 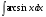 4. 4. 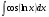 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
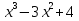
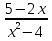
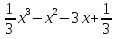
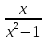
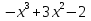
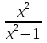
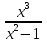
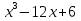
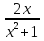
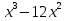 -9x+1
-9x+1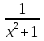
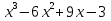
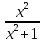
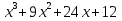
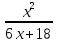
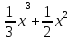 -2x-
-2x-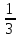
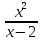
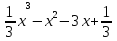
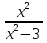
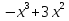 +9x-
+9x-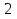
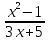
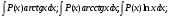
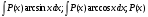 - многочлен.
- многочлен. 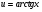
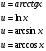
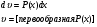
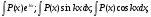
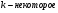
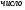
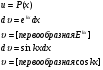
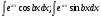 а и b некоторые числа.
а и b некоторые числа.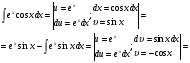
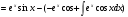 .
.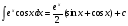 .
.