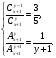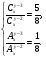Учебник для студентов образовательных учреждений спо/С. Г. Григорьев, С. В. Иволгина; под редакцией В. А. Гусева 10-е изд., стер. М.: Издательский центр «Академия». 2014. 416 с
 Скачать 205.17 Kb. |
Методические указания по проведениюпрактической работы № 6Решение простейших задач теории вероятностейЦель работы: Используя теоретический материал и образцы решения задач, решить примеры по теме «Решение простейших задач теории вероятностей» Перечень справочной литературы :
Краткие теоретические сведения: Теория вероятности Случайные события. Частота. Вероятность Теория вероятностей — математическая наука, изучающая закономерности массовых случайных явлений (событий). Случайным событием (или просто событием) называется всякое явление, которое может произойти или не произойти при осуществлении определенной совокупности условий. Теория вероятностей имеет дело с такими событиями, которые имеют массовый характер. Это значит, что данная совокупность условий может быть воспроизведена неограниченное число раз. Каждое такое осуществление данной совокупности условий называют испытанием (или опытом). Если, например, испытание состоит в бросании монеты, то выпадение герба является событием; если испытание — изготовление подшипника данного типа, то соответствие подшипника стандарту — событие; если испытание — бросание игральной кости, т. е. кубика, на гранях которого проставлены цифры (очки) от 1 до 6, то выпадение пятерки — событие. События будем обозначать заглавными буквами латинского алфавита: A, В, С, ... Пусть при n испытаниях событие A появилось m раз. Отношение m/n называется частотой (относительной частотой) события A и обозначается Р*(А)=m/n Опыт показывает, что при многократном повторении испытаний частота Р*(А) случайного события обладает устойчивостью. Событие называется достоверным, если оно в данном опыте обязательно должно произойти; наоборот, событие называется невозможным, если оно в данном опыте не может произойти. Пусть, например, из урны, содержащей только черные шары, вынимают шар. Тогда появление черного шара — достоверное событие; появление белого шара — невозможное событие. Если событие достоверно, то оно произойдет при каждом испытании (m=n). Поэтому частота достоверного события всегда равна единице. Наоборот, если событие невозможно, то оно ни при одном испытании не осуществится (m=0). Следовательно, частота невозможного события в любой серии испытаний равна нулю. Поэтому вероятность достоверного события равна единице, а вероятность невозможного события равна нулю. Если событие A не является ни достоверным, ни невозможным, то его частота m/n при большом числе испытаний будет мало отличаться от некоторого числа p (где 0 < p < 1 ) — вероятности события A. Совмещением (или произведением) двух событий A и В называется событие, состоящее в совместном наступлении как события A, так и события В. Это событие будем обозначать АВ или ВА. Аналогично, совмещением нескольких событий, например A, В и С, называется событие D=ABC, состоящее в совместном наступлении событий A, В и С. Объединением (или суммой) двух событий A и В называется событие С, заключающееся в том, что произойдет по крайней мере одно из событий A или В. Это событие обозначается так: С=А+В. Объединением нескольких событий называется событие, состоящее в появлении по крайней мере одного из них. Запись D=A+B+C означает, что событие D есть объединение событий A, В и С. Два события A и В называются несовместными, если наступление события A исключает наступление события В. Отсюда следует, что если события A и В несовместны, то событие AB — невозможное. Аксиомы вероятностей Пусть A и B — два несовместных события, причем в n испытаниях событие A произошло m1 раз, а событие В произошло m2 раз. Тогда частоты событий A и В соответственно равны P*(A)=m1/n, P*(B)=m2/n. Так как события A и В несовместны, то событие A+B в данной серии опытов произошло m1+m2 раз. Следовательно,  Таким образом, частота события A+B равна сумме частот событий A и В. Но при больших n частоты P*(A), P*(B) и P*(A+B) мало отличаются от соответствующих вероятностей P(A), P(B) и P(A+B). Поэтому естественно принять, что если A и В — несовместные события, то P(A+B)=P(A)+P(B) Изложенное позволяет высказать следующие свойства вероятностей, которые мы принимаем в качестве аксиом. Аксиома 1. Каждому случайному событию A соответствует определенное число Р(А), называемое его вероятностью и удовлетворяющее условию  .Аксиома 2. Вероятность достоверного события равна единице. Аксиома 3 (аксиома сложения вероятностей). Пусть A и В — несовместные события. Тогда вероятность того, что произойдет хотя бы одно из этих двух событий, равна сумме их вероятностей:
Аксиома 3 допускает обобщение на случай нескольких событий, а именно: если события A1, A2, ..., An, попарно несовместны, то
Событием, противоположным событию  , называется событие  , состоящее в ненаступлении события . Очевидно, события и несовместны.Пусть, например, событие состоит в том, что изделие удовлетворяет стандарту; тогда противоположное событие заключается в том, что изделие стандарту не удовлетворяет. Пусть событие — выпадение четного числа очков при однократном бросании игральной кости; тогда — выпадение нечетного числа очков.Теорема 1. Для любого события вероятность противоположного события выражается равенством
Доказательство. Событие +, состоящее в наступлении или события , или события , очевидно, является достоверным. Поэтому на основании аксиомы 2 имеем Р(+)=1. Так как события и несовместны, то используя аксиому 3, получим Р(+)=Р()+P(). Следовательно, Р()+P()=1, откуда  .Теорема 2. Вероятность невозможного события равна нулю. Доказательство непосредственно следует из аксиомы 2 и теоремы 1, если заметить, что невозможное событие противоположно достоверному событию. Классическое определение вероятности Как было сказано выше, при большом числе n испытаний частота P*(A)=m/n появления события A обладает устойчивостью и дает приближенное значение вероятности события A, т.е.  .Это обстоятельство позволяет находить приближенно вероятность события опытным путем. Практически такой способ нахождения вероятности события не всегда удобен. В ряде случаев вероятность события удается определить до опыта с помощью понятия равновероятности событий (или равновозможности). Два события называются равновероятными (или равновозможными), если нет никаких объективных причин считать, что одно из них может наступить чаще, чем другое. Так, например, появления герба или надписи при бросании монеты представляют собой равновероятные события. Рассмотрим другой пример. Пусть бросают игральную кость. В силу симметрии кубика можно считать, что появление любой из цифр 1, 2, 3, 4, 5 или 6 одинаково возможно (равновероятно). События E1,E2, ..., EN в данном опыте образуют полную группу, если в результате опыта должно произойти хотя бы одно из них. Так, в последнем примере полная группа событий состоит из шести событий — появлений цифр 1, 2, 3, 4, 5 и 6. Очевидно, любое событие A и противоположное ему событие образуют полную группу.Событие B называется благоприятствующим событию A, если наступление события B влечет за собой наступление события A. Так, если A — появление четного числа очков при бросании игральной кости, то появление цифры 4 представляет собой событие, благоприятствующее событию A. Пусть события E1,E2, ..., EN в данном опыте образуют полную группу равновероятных и попарно несовместных событий. Будем называть их исходами испытания. Предположим, что событию A благоприятствуют M исходов испытания. Тогда вероятностью события A в данном опыте называют отношение M/N. Итак, мы приходим к следующему определению. Вероятностью P(A) события в данном опыте называется отношение числа M исходов опыта, благоприятствующих событию A, к общему числу N возможных исходов опыта, образующих полную группу равновероятных попарно несовместных событий:  Это определение вероятности часто называют классическим. Можно показать, что классическое определение удовлетворяет аксиомам вероятности. Пример 1. На завод привезли партию из 1000 подшипников. Случайно в эту партию попало 30 подшипников, не удовлетворяющих стандарту. Определить вероятность P(A) того, что взятый наудачу подшипник окажется стандартным. Решение: Число стандартных подшипников равно 1000—30=970. Будем считать, что каждый подшипник имеет одинаковую вероятность быть выбранным. Тогда полная группа событий состоит из N=1000 равновероятных исходов, из которых событию A благоприятствуют М=970 исходов. Поэтому P(A)=M/N=970/1000=0.97 Пример 2. В урне 10 шаров: 3 белых и 7 черных. Из урны вынимают сразу два шара. Какова вероятность р того, что оба шара окажутся белыми? Решение: Число N всех равновероятных исходов испытания равно числу способов, которыми можно из 10 шаров вынуть два, т. е. числу сочетаний из 10 элементов по 2:  Число благоприятствующих исходов:  Следовательно, искомая вероятность  Пример 3. В урне 2 зеленых, 7 красных, 5 коричневых и 10 белых шаров. Какова вероятность появления цветного шара? Решение: Находим соответственно вероятности появления зеленого, красного и коричневого шаров: Р(зел.)=2/24; Р(кр.)=7/24; Р(кор.)=5/24. Так как рассматриваемые события, очевидно, несовместны, то, применяя аксиому сложения, найдем вероятность появления цветного шара:  Условная вероятность. Теорема умножения вероятностей Во многих задачах приходится находить вероятность совмещения событий А и В, если известны вероятности событий А и В. Рассмотрим следующий пример. Пусть брошены две монеты. Найдем вероятность появления двух гербов. Мы имеем 4 равновероятных попарно несовместных исхода, образующих полную группу:
Таким образом, P(герб,герб)=1/4. Пусть теперь нам стало известно, что на первой монете выпал герб. Как изменится после этого вероятность того, что герб появится на обеих монетах? Так как на первой монете выпал герб, то теперь полная группа состоит из двух равновероятных несовместных исходов:
При этом только один из исходов благоприятствует событию (герб, герб). Поэтому при сделанных предположениях Р(герб,герб)=1/2. Обозначим через А появление двух гербов, а через В — появление герба на первой монете. Мы видим, что вероятность события А изменилась, когда стало известно, что событие B произошло. Новую вероятность события А, в предположении, что произошло событие B, будем обозначать PB(А). Таким образом, Р(A)=1/4; PB(А)=1/2 Теорема умножения. Вероятность совмещения событий А и В равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие осуществилось, т. е.
Доказательство. Докажем справедливость соотношения (4), опираясь на классическое определение вероятности. Пусть возможные исходы Е1, Е2, ..., ЕN данного опыта образуют полную группу равновероятных попарно несовместных событий, из которых событию A благоприятствуют M исходов, и пусть из этих M исходов L исходов благоприятствуют событию B. Очевидно, что совмещению событий A и B благоприятствуют L из N возможных результатов испытания. Это дает  ;  ;  Таким образом,  Поменяв местами A и B, аналогично получим
Из формул (4) и (5) имеем
Теорема умножения легко обобщается на любое , конечное число событий. Так, например, в случае трех событий A1, A2, A3 имеем *  В общем случае
Введем теперь следующее определение. Два события A и B называются независимыми, если предположение о том, что произошло одно из них, не изменяет вероятность другого, т. е. если
Из соотношения (6) вытекает, что из двух равенств (8) одно является следствием другого. Пусть, например, событие A — появление герба при однократном брссании монеты, а событие B — появление карты бубновой масти при вынимании карты из колоды. Очевидно, что события A и B независимы. В случае независимости событий A к B формула (4) примет более простой вид:
т. е. вероятность совмещения двух независимых событий равна произведению вероятностей этих событий. События А1, А2, ..., Аn называются независимыми в совокупности, если вероятность наступления каждого из них не меняет своего значения после того, как одно или несколько из остальных событий осуществились. Исходя из этого определения, в случае независимости событий А1, А2, ..., Аn между собой в совокупности на основании формулы (7) имеем
Пример 1. Какова вероятность того, что при десятикратном бросании монеты герб выпадет 10 раз? Решение: Пусть событие Ai — появление герба при i-м бросании. Искомая вероятность есть вероятность совмещения всех событий Ai (i=1,2,3,...,10), а так как они, очевидно, независимы в совокупности, то применяя формулу (10), имеем  Но P(Ai)=1/2 для любого i; поэтому 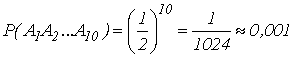 Пример 2. Рабочий обслуживает три станка, работающих независимо друг от друга. Вероятность того, что в течение часа станок не потребует внимания рабочего, для первого станка равна 0,9, для второго — 0,8, для третьего — 0,7. Найти: 1) вероятность р того, что в течение часа ни один из трех станков не потребует внимания рабочего; 2) вероятность того, что в течение часа по крайней мере один из станков не потребует внимания рабочего. Решение: 1) Искомую вероятность р находим по формуле (10):  2) Вероятность того, что в течение часа станок потребует внимания рабочего для первого станка равна 1—0,9=0,1, для второго и для третьего станков она соответственно равна 1—0,8=0,2 и 1—0,7=0,3. Тогда вероятность того, что в течение часа все три станка потребуют внимания рабочего, на основании формулы (10) составляет  Событие A, заключающееся в том, что в течение часа все три станка потребуют внимания рабочего, противоположно событию  , состоящему в том, что по крайней мере один из станков не потребует внимания рабочего. Поэтому по формуле (3) получаем  Пример 3. Из урны, содержащей 3 белых и 7 черных шаров, вынимают два шара. Какова вероятность того, что оба шара окажутся белыми ? Решение: Эта задача уже была решена в п. 3 с помощью классического определения вероятности. Решим ее, применяя формулу (5). Извлечение двух шаров равносильно последовательному их извлечению. Обозначим через А появление белого шара при первом извлечении, а через В — при втором. Событие, состоящее в появлении двух белых шаров, является совмещением событий А и В. По формуле (5) имеем  Но Р(А)=3/10; РA(В)=2/9, поскольку после того, как был вынут первый белый шар, в урне осталось 9 шаров, из которых 2 белых. Следовательно,  Формула полной вероятности Пусть событие A может произойти только вместе с одним из попарно несовместных событий H1, H2, ..., Hn, образующих полную группу. Тогда, если произошло событие A, то это значит, что произошло одно из попарно несовместных событий H1A, H2A, ..., HnA. Следовательно,  Применяя аксиому сложения вероятностей, имеем  Но  (i=1, 2, ..., n), поэтому
Эта формула называется формулой полной вероятности. События H1, H2, ..., Hn часто называют «гипотезами». Пример. В магазин поступили электрические лампочки одного типа, изготовленные на четырех ламповых заводах: с 1-го завода 250 шт., со 2-го — 525 шт., с 3-го — 275 шт. и с 4-го — 950 шт. Вероятность того, что лампочка прогорит более 1500 часов, для 1-го завода равна 0,15, для 2-го — 0,30, для 3-го — 0,20, для 4-го — 0,10. При раскладке по полкам магазина лампочки были перемешаны. Какова вероятность того, что купленная лампочка прогорит более 1500 часов? Решение: Пусть A — событие, состоящее в том, что лампочка прогорит более 1500 часов, а Н1, Н2, Н3 и Н4 — гипотезы, что она изготовлена соответственно 1, 2, 3 или 4-м заводом. Так как всего лампочек 2000 шт., то вероятности гипотез соответственно равны 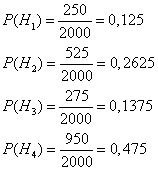 Далее, из условия задачи следует, что 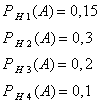 Используя формулу полной вероятности (11), имеем  Формула Бейеса Предположим, что производится некоторый опыт, причем об условиях его проведения можно высказать n единственно возможных и несовместных гипотез  , имеющих вероятности  . Пусть в результате опыта может произойти или не произойти событие А, причем известно, что если опыт происходит при выполнении гипотезы  , то   Спрашивается, как изменятся вероятности гипотез, если стало известным, что событие А произошло? Иными словами, нас интересуют значения вероятностей  На основании соотношений (4) и (5) имеем  откуда  Но по формуле полной вероятности 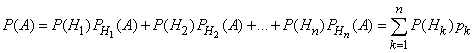 Поэтому
Формула (12) называется формулой Бейеса*. Пример. На склад поступило 1000 подшипников. Из них 200 изготовлены на 1-м заводе, 460—на 2-м и 340 - на 3-м. Вероятность того, что подшипник окажется нестандартным, для 1-го завода равна 0,03, для 2-го — 0,02, для 3-го — 0,01. Взятый наудачу подшипник оказался н естандартным. Какова вероятность того, что он изготовлен 1-м заводом? Решение: Пусть A — событие, состоящее в том, что взятый Подшипник нестандартный, а 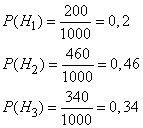 - гипотезы, что он изготовлен соответственно 1-м, 2-м или 3-м заводом. Вероятности указанных гипотез составляют  Из условия задачи следует, что 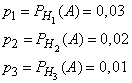 Найдем  , т. е. вероятность того, что подшипник, оказавшийся нестандартным, изготовлен 1-м заводом. По формуле Бейеса имеем  Таким образом, вероятность гипотезы, что подшипник изготовлен 1-м заводом, изменилась после того, как стало известно, что он нестандартен. Последовательные испытания. Формула Бернули Предположим, что производится n независимых испытаний, в результате каждого из которых может наступить или не наступить некоторое событие A. Пусть при каждом испытании вероятность наступления события А равна P(A)=p и, следовательно, вероятность противоположного события (ненаступления А) равна  . Определим вероятность Pn(m) того, что событие А произойдет m раз при n испытаниях. При этом заметим, что наступления или ненаступления события А могут чередоваться различным образом. Условимся записывать возможные результаты испытаний в виде комбинаций букв А и . Например, запись  означает, что в четырех испытаниях событие осуществилось в 1-м и 4-м случаях и не осуществилось во 2-м и 3-м случаях.Всякую комбинацию, в которую А входит m раз и входит n-m раз, назовем благоприятной. Количество благоприятных комбинаций равно количеству k способов, которыми можно выбрать m чисел из данных n; таким образом, оно равно числу сочетаний из n элементов по m, т.е.  Подсчитаем вероятности благоприятных комбинаций. Рассмотрим сначала случай, когда событие A происходит в первых m испытаниях и, следовательно, не происходит в остальных n-m испытаниях. Такая благоприятная комбинация имеет следующий вид: 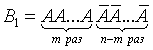 Вероятность этой комбинации в силу независимости испытаний (на основании теоремы умножения вероятностей) составляет 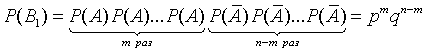 Так как в любой другой благоприятной комбинации Вi событие A встречается также m раз, а событие происходит n-m раз, то вероятность каждой из таких комбинаций также равна  . Итак  Все благоприятные комбинации являются, очевидно, несовместными. Поэтому (на основании аксиомы сложения вероятностей)  Следовательно,
Формула (13) называется формулой Бернулли *. Пример 1. Вероятность попадания в цель при одном выстреле равна 0,6. Какова вероятность того, что 8 выстрелов дадут 5 попаданий? Решение: Здесь n=8; m=5; p=0,6; q=1-0,6=0,4. Используя формулу (13'), имеем  Пример 3. Игральную кость бросают 80 раз. Определить вероятность того, что цифра 3 появится 20 раз. Решение: Здесь m=20; n=80; p=1/6; q=1-1/6=5/6; далее находим 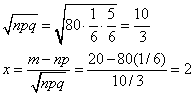 Используя формулу (15), получим  так как из табличного значения находим, что  1. Дано: В партии из 23 деталей находятся 10 бракованных. Вынимают из партии наудачу две детали. Используя классическое определение теории вероятности определить, какова вероятность того, что обе детали окажутся бракованными. Решение: Число N всех равновероятных исходов испытания равно числу способов, которыми можно из 23 деталей вынуть две, т.е. числу сочетаний из 23 элементов по 2:  Число благоприятных исходов  Cледовательно, искомая вероятность  2. Дано: В ящике лежат шары: 4 белых, 10 красных, 8 зеленых, 9 коричневых. Из ящика вынимают один шар. Пользуясь теоремой сложения вероятностей определить, какова вероятность, что шар окажется цветным (не белым) ? Решение: Всего в ящике лежит N=4+10+8+9=31 шар. Вероятность вытащить красный шар  Вероятность вытащить зеленый шар  Вероятность вытащить коричневый шар  Т.к. эти три события несовместны, то пользуясь теоремой сложения вероятностей определим вероятность того, что шар окажется цветным (не белым)  3. Дано: В вопросах к зачету имеются 75% вопросов, на которые студенты знают ответы. Преподаватель выбирает из них два вопроса и задает их студенту. Определить вероятность того, что среди полученных студентом вопросов есть хотя бы один, на который он знает ответ Решение: Вероятность вытащить знакомый вопрос p=0.75, незнакомый q=1-p=1-0.75=0.25 Пусть H1 - гипотеза, что студент не знает ни одного из 2-х вопросов. Вероятность этой гипотезы:  Искомая вероятность соответственно равна:  4. Дано: На складе находятся 26 деталей из которых 13 стандартные. Рабочий берет наугад две детали. Пользуясь теоремой умножения вероятностей зависимых событий определить вероятность того, что обе детали окажутся стандартными. Решение: Извлечение двух деталей равносильно последовательному их извлечению. Обозначим через A - появление стандартной детали при первом извлечении, а через B - при втором. Событие, состоящее в извлечении двух стандартных деталей, является совмещением событий А и B. Пользуясь теоремой умножения вероятностей имеем:  , где  Поскольку после того, как была вынута первая стандартная деталь на складе осталось 25 деталей, из которых 12 стандартных, то  , тогда  5. Дано: В сборочный цех поступили детали с трех станков. На первом станке изготовлено 51% деталей от их общего количества, на втором станке 24% и на третьем 25%. При этом на первом станке было изготовлено 90% деталей первого сорта, на втором 80% и на третьем 70%. Используя формулу полной вероятности определить, какова вероятность того, что взятая наугад деталь окажется первого сорта ? Решение: Пусть A - cобытие, состоящее в том, что взятая деталь окажется первого сорта, а H1, H2 и H3 - гипотезы, что она изготовлена соответственно на 1, 2 и 3 станке. Вероятности этих гипотез соответственно равны: 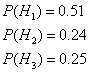 далее, из условия задачи следует, что: 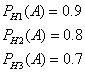 Используя формулу полной вероятности, получим искомую вероятность  6. Дано: Имеется три одинаковых по виду ящика. В первом ящике находится 26 белых шаров, во втором 15 белых и 11 черных, в третьем ящике 26 черных шаров. Из выбранного наугад ящика вынули белый шар. Используя формулу Байеса вычислить вероятность того, что белый шар вынут из первого ящика. Решение: Пусть A - cобытие, состоящее в том, что взятый шар окажется белым, а H1 и H2 - гипотезы, что он был взят из 1-го и 2-го ящика. (Третий ящик рассматривать не будем, т.к. там только черные шары, а из условий известно, что вынут именно белый шар.) Вероятности указанных гипотез соответственно равны: 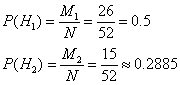 , здесь N=26+15+11=52 - количество шаров в 1-м и 2-м ящиках Из условия задачи следует, что: 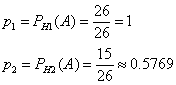 Найдем PA(H1), т.е. вероятность того, что вынутый белый шар был взят из 1-го ящика.  7. Дано: Вероятность изготовления нестандартной детали равна 0.11. Пользуясь формулой Бернулли найти вероятность того, что из пяти наудачу взятых деталей будут четыре стандартных. Решение: Формула Бернулли:  В соответствии с исходными данными, здесь: q=0.11 p=1-q=1-0.11=0.89 n=5 m=4 Используя формулу Бернулли получим:  Варианты заданий Вариант 1
полосатый флаг, если имеется материал 5 различных цветов?
при условии, что каждая цифра может содержаться в записи числа лишь нечетное число раз? 3. Решите уравнение 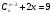 .4. Из колоды в 36 карт вытаскивают две карты. Какова вероятность извлечь при этом 2 туза? Вариант 2 1. В яхт-клубе состоит 9 человек. Из них надо выбрать председателя, заместителя, секретаря и казначея. Сколькими способами это можно сделать?
при условии, что каждая цифра может содержаться в записи числа лишь 1 раз?
Вариант 3
из 4 человек для участия в четырехэтапной эстафете, но и определить порядок выхода спортсменов на этапы. Сколькими способами это можно сделать?
при условии, что цифры могут повторяться?
Вариант 4 1. В городской думе 30 человек. Из них надо выбрать председателя и трех его заместителей. Сколькими способами это можно сделать?
Вариант 5 1.Сколькими способами можно выбрать из полной колоды, содержащей 36 карт, 4 карты разных мастей при условии, что среди вынутых карт нет ни одной пары карт одинакового достоинства?
при условии, что одна и только одна цифра содержится в записи числа четное число раз?
Вариант 6 1. В классе 15 девочек и 17 мальчиков. Для дежурства на избирательном участке надо выделить трех девочек и двух мальчиков. Сколькими способами это можно сделать?
при условии, что одна и только одна цифра содержится в записи числа четное число раз?
|
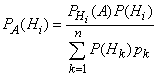
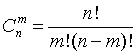
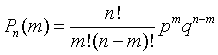
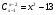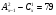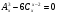и 
.
.
.
