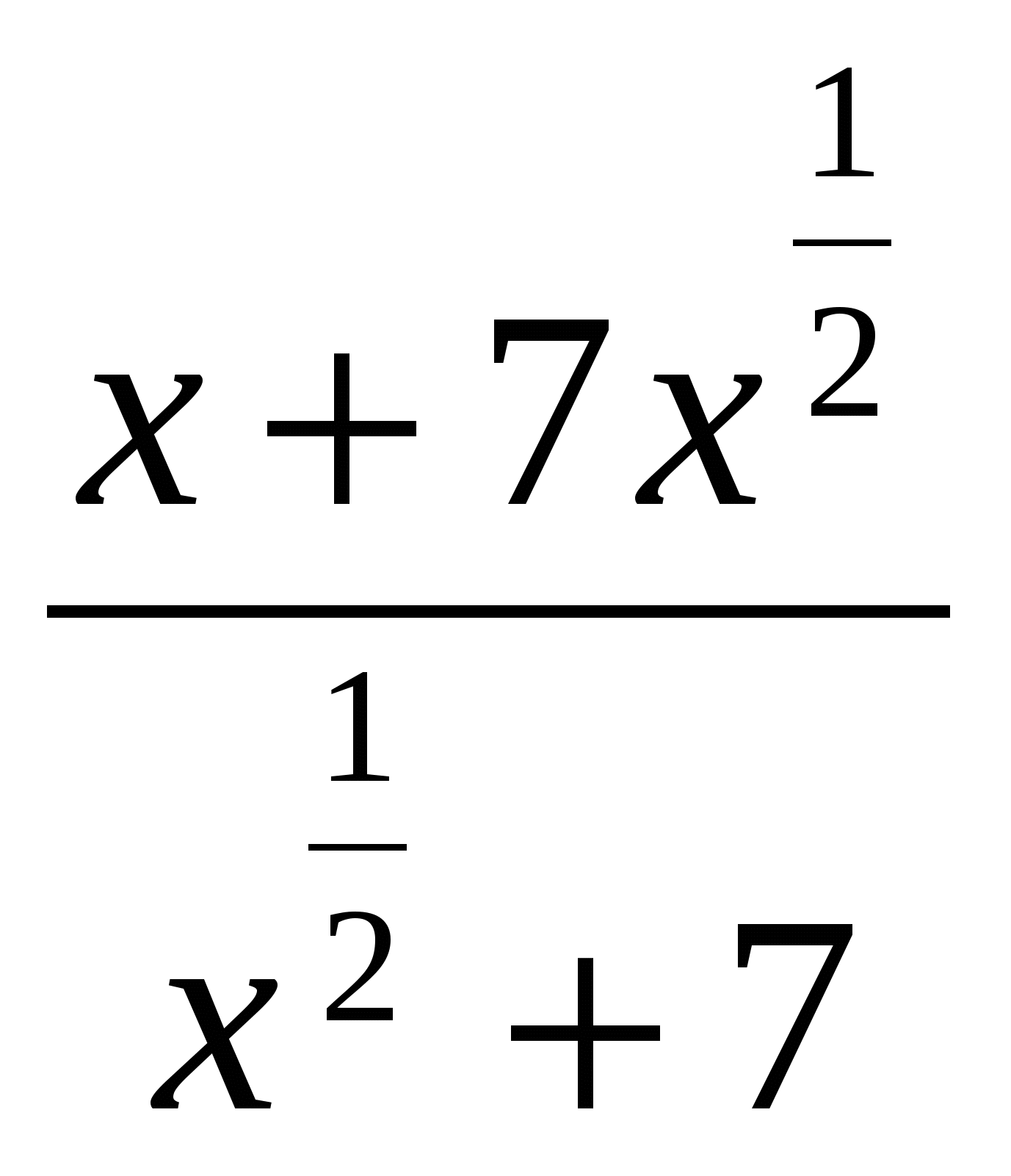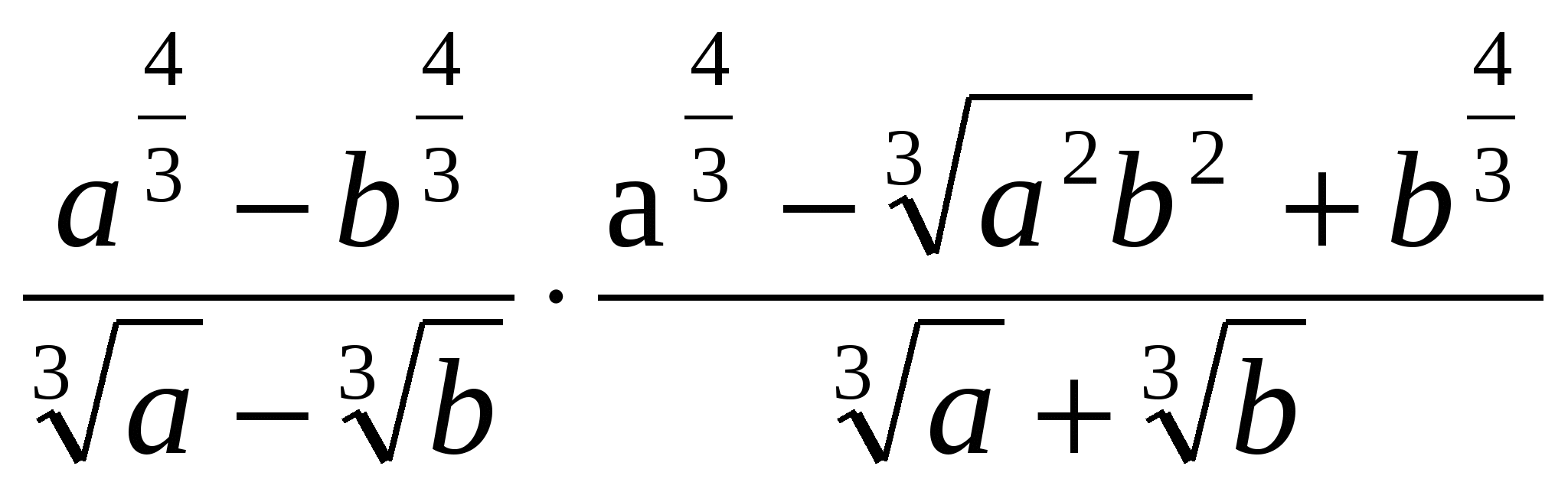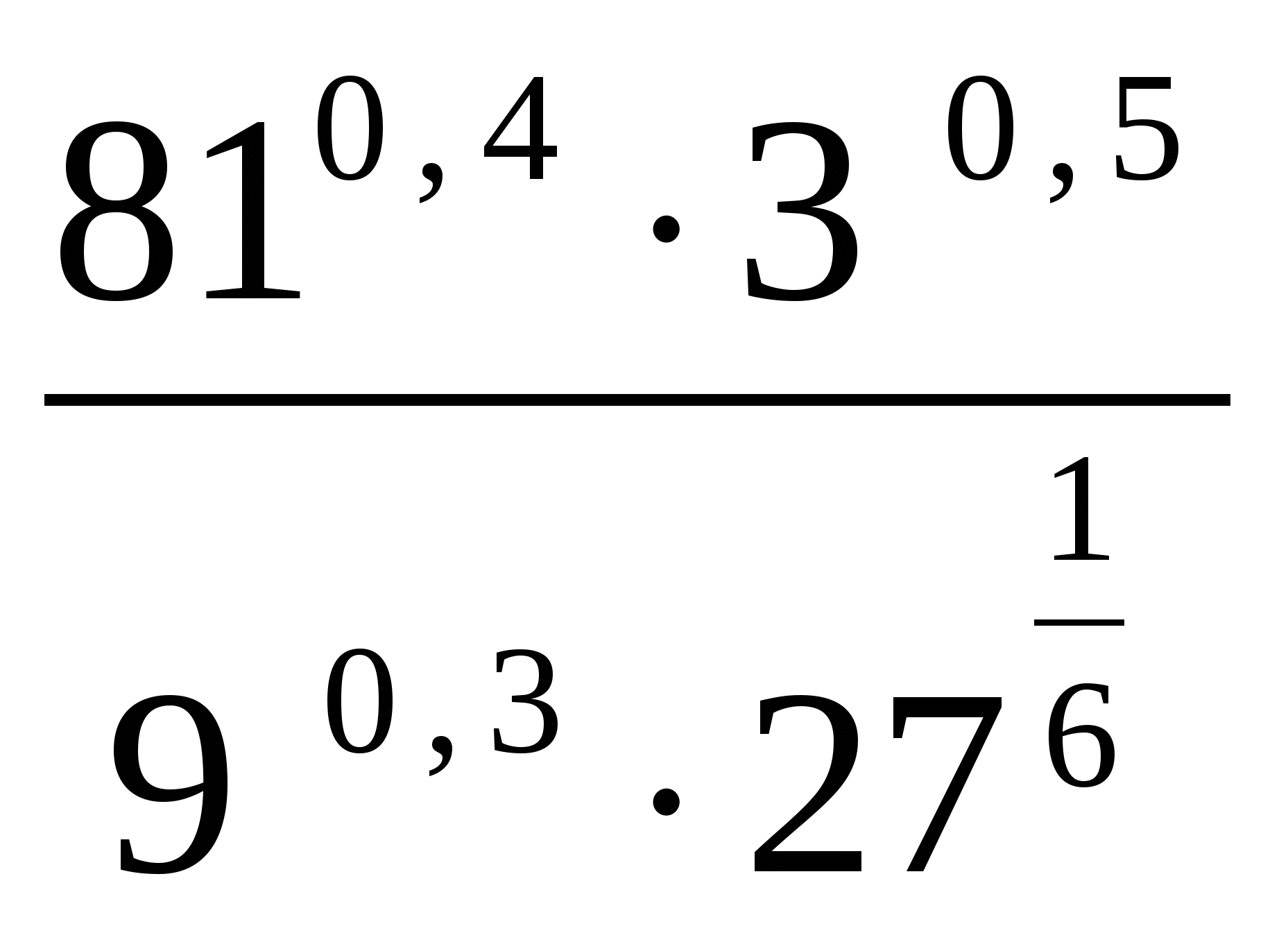Пояснительная записка
 Скачать 188.05 Kb.
|
Естественно-математическое образование в системе общего среднего образования, занимает одно из ведущих мест. Математика, являясь обязательной составной частью всеобщего среднего образования, одновременно образует прочный фундамент всего естествознания. Включение ее в качестве основного учебного предмета в школьный учебный процесс ни у кого не вызывает сомнения. На сегодняшний день, в соответствии с Базисным учебным планом, на ее изучение в рамках курса 10 класса отводится 5 часов в неделю (на изучение алгебры и начал анализа – 3 учебных часа в неделю, геометрии – 2 часа), что составляет 170 часов за год. Назначение математического образования можно охарактеризовать с двух сторон: практической, связанной с созданием и применением инструментария, необходимого человеку в его продуктивной деятельности и духовной, связанной с мышлением человека, с овладения определенным методом познания и преобразованием мира математическим методом. Практическая полезность математики обусловлена тем, что ее предметом являются фундаментальные структуры реального мира. Без конкретных математических знаний затруднено понимание принципов устройства и использования современной техники, восприятие научных знаний, интерпретация разнообразной социальной, экономической, политической информации, малоэффективна повседневная практическая деятельность. С другой стороны математическое образование вносит свой вклад в формирование общей культуры человека, способствует эстетическому воспитанию, пониманию красоты и изящества математических рассуждений, восприятию геометрических форм, усвоению идей симметрии. Таким образом, без базовой математической подготовки невозможна постановка образования современного человека. Роль математики в развитии общества в целом и формировании личности каждого отдельного человека определяет цели и задачи обучения математике в общеобразовательной школе:
Цель изучения курса алгебры и начал анализа в Х-ХI классах - систематическое изучение функции, как важнейшего математического объекта средствами алгебры и математического анализа, раскрытие политехнического и прикладного значения общих методов математики, связанных с исследованием функций, подготовка необходимого аппарата для изучения геометрии и физики. Рабочая программа ориентирована на усвоение обязательного минимума математического образования, позволяет работать без перегрузок в классе с детьми разного уровня обучения и интереса к математике. В процессе реализации рабочей программы решаются не только задачи общего математического образования, но и дополнительные, направленные на:
В основе построения программы лежат принципы единства, преемственности, вариативности, выделения понятийного ядра, деятельностного подхода, системности. Основные разделы: курс «Алгебра и начала анализа. 10 класс»: «Действительные числа», «Степенная функция», «Показательная функция», «Логарифмическая функция», «Тригонометрические формулы», «Тригонометрические уравнения», «Итоговое повторение»; Курс алгебры и начал анализа X класса характеризуется содержательным раскрытием понятий, утверждений и методов, относящихся к началам анализа, выявлением их практической значимости. При изучении вопросов анализа широко используются наглядные соображения. Уровень строгости изложения определяется с учетом общеобразовательной направленности изучения начал анализа и согласуется с уровнем строгости приложений изучаемого материала в смежных дисциплинах. Характерной особенностью курса является систематизация и обобщение знаний учащихся, закрепление и развитие умений и навыков учащихся, полученных в курсе алгебры, что осуществляется как при изучении нового материала, так и при проведении обобщающего повторения. Принципиальным положением организации математического образования становится дифференциация обучения в школе. При этом достижение уровня обязательной подготовки становится непременной обязанностью ученика в его учебной работе. В организации учебно-воспитательного процесса важную роль играют задачи. В обучении математики они являются и целью, и средством обучения и математического развития школьников. Организуя решение задач, следует иметь в виду, что теоретический материал осознается и осваивается преимущественно в процессе решения задач, организуя их решение, целесообразно использовать дифференцированный подход к учащимся, основанный на достижении обязательного уровня подготовки. Это способствует нормализации нагрузки школьников, обеспечивая их посильной работой, и формирует у них положительное отношение к учебе. Важным условием правильной организации учебно-воспитательного процесса является выбор рациональной системы методов и приемов обучения. Необходимо реализовать сбалансированное сочетание традиционных и новых методов обучения, оптимизировать применение объяснительно-иллюстративных и эвристических методов, использование технических средств. Учебный процесс необходимо ориентировать на рациональное сочетание устных и письменных видов работы, как при изучении теории, так и при решении задач. Внимание должно быть направлено на развитие речи учащихся, формирование у них навыков умственного труда - планирование своей работы, поиск рациональных путей ее выполнения, критическую оценку результатов. В школе математика является опорным предметом средней школы: она обеспечивает изучение других дисциплин, прежде всего предметов естественно-научного цикла, в частности физики, основ информатики и вычислительной техники, химии. Например, на уроках физики, изучение понятий и законов механики осуществляется с использованием знаний о векторах, действиях с ними, координатах точки, проекциях вектора, линейной функции и ее графике, квадратных уравнениях, окружности, касательной к ней. Практические умения и навыки математического характера необходимы для трудовой подготовки школьников. При изучении отдельных тем курса математики возможна опора на знания, полученные учащимися на других предметах. Например, знания, полученные при изучении механики: о мгновенной скорости развиваются при введении производной; о свободных колебаниях - используются при рассмотрении дифференциальных уравнений; о перемещении в равноускоренном движении, о работе переменной силы – при изучении интеграла. Требования к математической подготовке учащихся: Вычисления и преобразования: В результате изучения курса математики учащиеся должны:
Уравнения и неравенства: В результате изучения курса математики учащиеся должны:
Функции: В результате изучения курса математики учащиеся должны:
Требования к уровню усвоения дисциплины. Рекомендации по оценке знаний, умений и навыков учащихся по математике. Опираясь на эти рекомендации, учитель оценивает знания, умения и навыки учащихся с учетом их индивидуальных особенностей.
Погрешность считается ошибкой, если она свидетельствует о том, что ученик не овладел основными знаниями, умениями, указанными в программе. К недочетам относятся погрешности, свидетельствующие о недостаточно полном или недостаточно прочном усвоении основных знаний и умений или об отсутствии знаний, которые в программе не считаются основными. Недочетами также считаются: погрешности, которые не привели к искажению смысла полученного учеником задания или способа его выполнения: неаккуратная запись, небрежное выполнение чертежа.
Ответ на теоретический вопрос считается безупречным, если по своему содержанию полностью соответствует вопросу, содержит все необходимые теоретические факты и обоснованные выводы, а его изложение и письменная запись математически грамотны и отличаются последовательностью и аккуратностью. Решение задачи считается безупречным, если правильно выбран способ решения, само решение сопровождается необходимыми объяснениями, верно, выполнены нужные вычисления и преобразования, получен верный ответ, последовательно и аккуратно записано решение.
Оценка устных ответов учащихся. Ответ оценивается отметкой «5», если ученик:
Возможны одна – две неточности при освещении второстепенных вопросов или в выкладках, которые ученик легко исправил по замечанию учителя. Ответ оценивается отметкой «4», если он удовлетворен в основном требованиям на отметку «5», но при этом имеет один из недостатков:
Отметка «3» ставится в следующих случаях:
Отметка «2» ставится в следующих случаях:
Оценка «1» ставится в случае, если:
Оценка письменных контрольных работ учащихся. Отметка «5» ставится в следующих случаях:
Отметка «4» ставится, если:
Отметка «3» ставится, если:
Отметка «2» ставится, если:
Отметка «1» ставится, если:
II. Тематическое планирование учебного материала. «Алгебра и начала анализа».
I I I. Информационно – методическое обеспечение Для учащихся: 1. Ш.А. Алимов, Ю.М. Колягин, Ю.В. Сидоров и др. « Алгебра и начала анализа» - учебник для 10 -11 классов общеобразовательных учреждений.- Москва : Просвещение, 2011г . 2. А.П. Карп «Сборник задач по алгебре и началам анализа 10 – 11 класс» .Москва: «Просвещение» 2011 год. 3. Шестаков С.А., Захаров П.И. ЕГЭ 2011. Математика. Задача С1/Под ред. А.Л. Семёнова и И.В. Ященко. – М.:МЦНМО, 2012. – 120с 4. Шестаков С.А., Захаров П.И. ЕГЭ 2011. Математика. Задача С2/Под ред. А.Л. Семёнова и И.В. Ященко. – М.:МЦНМО, 2012. – 120с 5. Шестаков С.А., Захаров П.И. ЕГЭ 2011. Математика. Задача С3/Под ред. А.Л. Семёнова и И.В. Ященко. – М.:МЦНМО, 2012. – 120с 6. Шестаков С.А., Захаров П.И. ЕГЭ 2011. Математика. Задача С4/Под ред. А.Л. Семёнова и И.В. Ященко. – М.:МЦНМО, 2012. – 120с 7. Шестаков С.А., Захаров П.И. ЕГЭ 2011. Математика. Задача С5/Под ред. А.Л. Семёнова и И.В. Ященко. – М.:МЦНМО, 2012. – 120с 8. Шестаков С.А., Захаров П.И. ЕГЭ 2011. Математика. Задача С6/Под ред. А.Л. Семёнова и И.В. Ященко. – М.:МЦНМО, 2012. – 120с 9. Лаппо, Л.Д. ЕГЭ 2011. Математика. Практикум по выполнению типовых тестовых заданий ЕГЭ/Л.Д.Лаппо, М.А. Попов. – М.: Издательство «Экзамен», 2012. – 63,  с. (Серия «ЕГЭ. Практикум»)10. ЕГЭ 2012. Математика. Типовые тестовые задания/ И.Р. Высоцкий, Д.Д. Гущин, П.И. Захаров, В.С. Панферов, С.Е. Посицельский, А.В. Семёнов, А.Л. Семёнов, М.А. Семёнова, И.Н. Сергеев, В.А. Смирнов, С.А. Шестаков, Д.Э.Шноль, И.В. Ященко; под ред. А.Л. Семёнова, И.В. Ященко. – М.: Издательство «Экзамен», 2012. – 55, с. (Серия «ЕГЭ 2011. Типовые тестовые задания»)11. ЕГЭ 2012. Математика: тренировочные задания/ Т.А. Корешкова, В.В. Мирошин, Н.В. Шевелёва. – М.: Эксмо, 2012. – 80 с. – (ЕГЭ. Тренировочные задания). 12. ЕГЭ – 2012. Математика: типовые экзаменационные варианты: 30 вариантов/под ред. А.Л.Семёнова, И.В. Ященко. – М.: Национальное образование, 2010. – 240 с. – (ЕГЭ-2011. ФИПИ – школе) Для учителя: 1. Г.И. Григорьева Пособие для учителя « Алгебра» 10 класс. Волгоград : « Учитель» 2011 год. 2. А.П. Карп «Сборник задач по алгебре и началам анализа 10 – 11 класс» .Москва: «Просвещение» 2011 год. 3. Шестаков С.А., Захаров П.И. ЕГЭ 2011. Математика. Задача С1/Под ред. А.Л. Семёнова и И.В. Ященко. – М.:МЦНМО, 2012. – 120с 4. Шестаков С.А., Захаров П.И. ЕГЭ 2011. Математика. Задача С2/Под ред. А.Л. Семёнова и И.В. Ященко. – М.:МЦНМО, 2012. – 120с 5. Шестаков С.А., Захаров П.И. ЕГЭ 2011. Математика. Задача С3/Под ред. А.Л. Семёнова и И.В. Ященко. – М.:МЦНМО, 2012. – 120с 6. Шестаков С.А., Захаров П.И. ЕГЭ 2011. Математика. Задача С4/Под ред. А.Л. Семёнова и И.В. Ященко. – М.:МЦНМО, 2012. – 120с 7. Шестаков С.А., Захаров П.И. ЕГЭ 2011. Математика. Задача С5/Под ред. А.Л. Семёнова и И.В. Ященко. – М.:МЦНМО, 2012. – 120с 8. Шестаков С.А., Захаров П.И. ЕГЭ 2011. Математика. Задача С6/Под ред. А.Л. Семёнова и И.В. Ященко. – М.:МЦНМО, 2012. – 120с 9. Лаппо, Л.Д. ЕГЭ 2011. Математика. Практикум по выполнению типовых тестовых заданий ЕГЭ/Л.Д.Лаппо, М.А. Попов. – М.: Издательство «Экзамен», 2012. – 63, с. (Серия «ЕГЭ. Практикум»)10. ЕГЭ 2012. Математика. Типовые тестовые задания/ И.Р. Высоцкий, Д.Д. Гущин, П.И. Захаров, В.С. Панферов, С.Е. Посицельский, А.В. Семёнов, А.Л. Семёнов, М.А. Семёнова, И.Н. Сергеев, В.А. Смирнов, С.А. Шестаков, Д.Э.Шноль, И.В. Ященко; под ред. А.Л. Семёнова, И.В. Ященко. – М.: Издательство «Экзамен», 2012. – 55, с. (Серия «ЕГЭ 2012. Типовые тестовые задания»)11. ЕГЭ 2012. Математика: тренировочные задания/ Т.А. Корешкова, В.В. Мирошин, Н.В. Шевелёва. – М.: Эксмо, 2012. – 80 с. – (ЕГЭ. Тренировочные задания). 12. ЕГЭ – 2012. Математика: типовые экзаменационные варианты: 30 вариантов/под ред. А.Л.Семёнова, И.В. Ященко. – М.: Национальное образование, 2012. – 240 с. – (ЕГЭ-2011. ФИПИ – школе) 13. Б.М. Ивлев, С.М. Саакян, С.И. Шварцбург « Дидактические материалы по алгебре и началам анализа» 10 класс. Москва «Просвещение» 2011 год. 14. Б.Г. Зив, В.А Гольдич Дидактические материалы по алгебре и началам анализа для 10 класса, СПб.: «Петроглиф», «Виктория плюс», 2011 15. Шабунин М.И. и др. Алгебра и начала анализа. Дидактические материалы для 10-11 кл., 4 изд., М.: Мнемозина, 2011.- 251с. 16. Н.Е. Федорова, М.В. Ткачева Изучение алгебры и начал анализа в 10-11 кл. – М.: Просвещение, 2010. – 205с. Программное обеспечение: 1. Алгебра и начала анализа 10-11 классы 2. Алгебра, 7-11 классы 3. Математика, 5-11 классы. Практикум 4. ПМК «Математика. Средняя школа. Ч 3» 5. Уроки алгебры Кирилла и Мефодия (10-11 классы) 6. Физикон. Математика: Алгебра 7. Физикон. Математика: Функции и графики Контрольная работа №1 по теме: «Действительные числа» Вариант №1. Обязательная часть
Дополнительная часть
Вариант №2. Обязательная часть
Дополнительная часть
Контрольная работа №2 по теме: «Степенная функция» Вариант №1. 1. Найти область определения функции  .2. Изобразить эскиз графика функции  .
Вариант №2
Контрольная работа №3 по теме: «Показательная функция» Вариант №1
1)  ; 2) .
В ответе укажите корень уравнения или сумму корней, если их несколько. Вариант №2 1. Решить уравнение:
2. Решить неравенство  .3. Решить систему уравнений  _ 4. Решить неравенство: 1)  ; 2) .55. Решить уравнение  .6. Решите уравнение:  . В ответе укажите корень уравнения или сумму корней, если их несколько. Контрольная работа №4 по теме: «Логарифмическая функция» Вариант №1 1. Вычислите:  .2. При каких значениях х имеет смысл выражение: а)  ;б)  3. Решите уравнение:  4. Упростите: 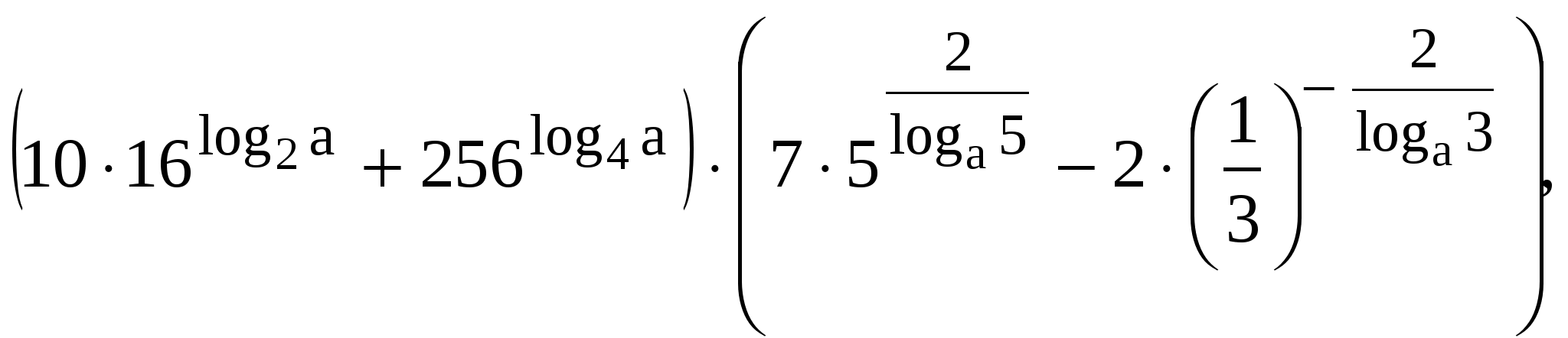 a0,a1.5. Дано:  . Найти:  .Вариант №2 1. Вычислите:  .2. При каких значениях x имеет смысл выражение: а)  б) 3. Решите уравнение:  4. Упростите:  a0,a1.5. Дано:  Найти:  Контрольная работа №5 по теме: «Тригонометрические формулы» Вариант №1 1. Решите уравнение:  .2. Упростите выражение: а)  ; б)  ;в)  .3. Пусть  углы треугольника. Докажите тождество: .Вариант №2 1. Решите уравнение:  .2. Упростите выражение: а)  ; б)  ;в)  .3. Пусть углы треугольника. Докажите тождество: .Контрольная работа №6 по теме: «Тригонометрические уравнения» Вариант №1 1. Решите уравнение: sin x -  =02. Решите уравнение: cos 2x=1 3. Укажите уравнение, которому соответствует решение:  :1) tg x = 1; 2) cos x = 0; 3) sin x = -1; 4) ctg x =  .4. На каком из рисунков показано решение неравенства: cos x <  ?1) 2) 3) 4) 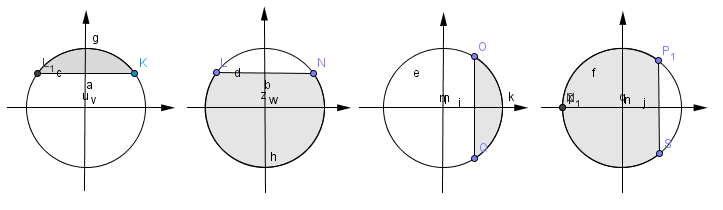 5. Решите неравенство: tg x ≥  :6. Решите уравнение: 6sin2 x + sin x – 1 = 0 7. Решите уравнение: 2sin2 x - sin 2x =0Вариант №2 1. Решите уравнение: sin x + =02. Решите уравнение: ctg (x+  )=3. Укажите уравнение, которому соответствует решение:  :1) ctg x = -1; 2) cos x = 0; 3) cos x = -1; 4) tg x = 1. 4. На каком из рисунков показано решение неравенства: sin x ≥ ?1 ) 2) 3) 4) 4) 5. Решите неравенство: ctg x ≥ 6. Решите уравнение: cos2 x - 4sin x + 3 = 0 7. Решите уравнение: sin2 x -3sin x cos x =0 |
; в несложных ситуациях применять производную для исследования функции на монотонность и экстремумы, для нахождения наибольших и наименьших значений функций и для построения графиков;
и 
.
.
; указать её область определения и множество значений. На одном рисунке построить графики данной функции и функции, обратной к данной.
.
.
и 
.
;
;
;
.
; указать её область определения и множество значений. На одном рисунке построить графики данной функции и функции, обратной к данной.
; 2)
.
.
.
.
; 2)
.