Контрольных работ по алгебре- 8, по геометрии-3, входящая к.р , за полугодие, за год по типу ЕГЭ-3. Итого:14 работ.
3. Содержание программы
воспитание средствами математики культуры личности, понимания значимости математики для научно-технического прогресса, отношения к математике как к части общечеловеческой культуры через знакомство с историей развития математики, эволюцией математических идей.
На основании требований Государственного образовательного стандарта 2004г. в содержании рабочей программы предполагается реализовать актуальные в настоящее время компетентностный, личностно-ориентированный, деятельностный подходы, которые определяют задачи обучения:
приобретение математических знаний и умений;
овладение обобщенными способами мыслительной, творческой деятельностей;
освоение компетенций: учебно-познавательной, коммуникативной, рефлексивной, личностного саморазвития, ценностно-ориентационной, смыслопоисковой и профессионально-трудового выбора.
Планируется использование следующих педагогических технологий в преподавании предмета:
технологии полного усвоения;
технологии обучения на основе решения задач;
технологии обучения на основе схематичных и знаковых моделей;
технологии проблемного обучения.
В течение года возможны коррективы рабочей программы, связанные с объективными причинами.
Требования к уровню подготовки учащихся (продвинутый уровень)
должны знать:
Корень степени n>1 и его свойства. Степень с рациональным показателем и ее свойства. Понятие о степени с действительным показателем. Свойства степени с действительным показателем.
Логарифм. Логарифм числа. Основное логарифмическое тождество. Логарифм произведения, частного, степени; переход к новому основанию. Десятичный и натуральный логарифмы, число е.
Преобразования простейших выражений, включающих арифметические операции, а также операцию возведения в степень и операцию логарифмирования.
Функции. Область определения и множество значений. График функции. Построение графиков функций, заданных различными способами. Свойства функций: монотонность, четность и нечетность, периодичность, ограниченность. Промежутки возрастания и убывания, наибольшее и наименьшее значения, точки экстремума (локального максимума и минимума). Графическая интерпретация. Примеры функциональных зависимостей в реальных процессах и явлениях. Степенная функция с натуральным показателем, ее свойства и график. Показательная функция (экспонента), ее свойства и график. Логарифмическая функция, ее свойства и график.
Преобразования графиков: параллельный перенос, симметрия относительно осей координат и симметрия относительно начала координат, симметрия относительно прямой y = x, растяжение и сжатие вдоль осей координат.
Первообразная. Понятие об определенном интеграле как площади криволинейной трапеции. Формула Ньютона-Лейбница. Примеры применения интеграла в физике и геометрии.
Уравнения и неравенства. Решение рациональных, показательных, логарифмических уравнений и неравенств. Решение иррациональных уравнений. Основные приемы решения систем уравнений: подстановка, алгебраическое сложение, введение новых переменных. Равносильность уравнений, неравенств, систем. Решение простейших систем уравнений с двумя неизвестными. Решение систем неравенств с одной переменной. Использование свойств и графиков функций при решении уравнений и неравенств. Метод интервалов. Изображение на координатной плоскости множества решений уравнений и неравенств с двумя переменными и их систем. Применение математических методов для решения содержательных задач из различных областей науки и практики. Интерпретация результата, учет реальных ограничений,
Многогранники. Призма, ее основания, боковые ребра, высота, боковая поверхность. Прямая и наклонная. призма. Правильная призма. Параллелепипед. Куб. Пирамида, ее основание, боковые ребра, высота, боковая поверхность. Треугольная пирамида. Правильная пирамида. Усеченная пирамида. Симметрии в кубе, в параллелепипеде, в призме и пирамиде. Понятие о симметрии в пространстве (центральная, осевая, зеркальная). Примеры симметрий в окружающем мире.Сечения куба, призмы, пирамиды. Представление о правильных многогранниках (тетраэдр, куб, октаэдр, додекаэдр и икосаэдр).
Тела и поверхности вращения. Цилиндр и конус. Усеченный конус. Основание, высота, боковая поверхность, образующая, развертка. Осевые сечения и сечения параллельные основанию. Шар и сфера, их сечения, касательная плоскость к сфере.
Объемы тел и площади их поверхностей. Понятие об объеме тела. Отношение объемов подобных тел.Формулы объема куба, прямоугольного параллелепипеда, призмы, цилиндра. Формулы объема пирамиды и конуса. Формулы площади поверхностей цилиндра и конуса. Формулы объема шара и площади сферы.
Координаты и векторы. Декартовы координаты в пространстве. Формула расстояния между двумя точками. Уравнения сферы и плоскости. Формула расстояния от точки до плоскости. Векторы. Модуль вектора. Равенство векторов. Сложение векторов и умножение вектора на число. Угол между векторами. Координаты вектора. Скалярное произведение векторов.
должны уметь (на продуктивном и творческом уровнях освоения):
выполнять арифметические действия, сочетая устные и письменные приемы, применение вычислительных устройств; находить значения корня натуральной степени, степени с рациональным показателем, логарифма, используя при необходимости вычислительные устройства; пользоваться оценкой и прикидкой при практических расчетах;
проводить по известным формулам и правилам преобразования буквенных выражений, включающих степени, радикалы, логарифмы;
вычислять значения числовых и буквенных выражений, осуществляя необходимые подстановки и преобразования;
определять значение функции по значению аргумента при различных способах задания функции;
строить графики изученных функций;
описывать по графику и в простейших случаях по формуле поведение и свойства функций, находить по графику функции наибольшие и наименьшие значения;
решать показательные и логарифмические уравнения, простейшие системы уравнений, используя свойства функций и их графиков;
вычислять производные и первообразные элементарных функций, используя справочные материалы;
исследовать в простейших случаях функции на монотонность, находить наибольшие и наименьшие значения функций, строить графики многочленов и простейших рациональных функций с использованием аппарата математического анализа;
вычислять в простейших случаях площади с использованием первообразной;
решать рациональные, показательные и логарифмические уравнения и неравенства, простейшие иррациональные уравнения, их системы;
использовать для приближенного решения уравнений и неравенств графический метод;
изображать на координатной плоскости множества решений простейших уравнений и их систем;
решать простейшие комбинаторные задачи методом перебора, а также с использованием известных формул;
распознавать на чертежах и моделях пространственные формы; соотносить трехмерные объекты с их описаниями, изображениями;
анализировать в простейших случаях взаимное расположение объектов в пространстве;
изображать основные многогранники и круглые тела; выполнять чертежи по условиям задач;
строить простейшие сечения куба, призмы, пирамиды;
решать планиметрические и простейшие стереометрические задачи на нахождение геометрических величин (длин, углов, площадей, объемов);
использовать при решении стереометрических задач планиметрические факты и методы;
проводить доказательные рассуждения в ходе решения задач;
владеть компетенциями: учебно – познавательной, ценностно – ориентационной, рефлексивной, коммуникативной, информационной, социально – трудовой.
Способны использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
практических расчетов по формулам, включая формулы, содержащие степени, радикалы, логарифмы, используя при необходимости справочные материалы и простейшие вычислительные устройства;
описания с помощью функций различных зависимостей, представления их графически, интерпретации графиков;
решения прикладных задач, в том числе социально-экономических и физических; построения и исследования простейших математических моделей. исследования (моделирования) несложных практических ситуаций на основе изученных формул и свойств фигур;
вычисления объемов и площадей поверхностей пространственных тел при решении практических задач, используя при необходимости справочники и вычислительные устройства.
Для обеспечения плодотворного учебного процесса предполагается использование информации и материалов следующих Интернет – ресурсов:
Министерство образования РФ:
https://ed.gov.ru/;
https://edu.ru/
Тестирование online: 5 - 11 классы:
https://kokch.kts.ru/cdo/
Мегаэнциклопедия Кирилла и Мефодия:
https://mega.km.ru
сайты «Энциклопедий энциклопедий», например:
https://rubricon.ru/;
https://encyclopedia.ru/
CD «1С: Репетитор. Математика. Часть1» (КиМ)
CD «ГЕОМЕТРИЯ не для отличников» (НИИ экономики авиационной промышленности)
«Математика, 5 - 11»
4. КАЛЕНДАРНО-ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ
№ урока
|
Тема
|
Дата
|
Количество часов.
|
Коррекция.
|
1.
|
Повторение курса геометрии 10 класса
|
|
|
|
2.
|
Тригонометрические функции. Тригонометрические уравнения. Преобразование тригонометрических выражений
|
|
|
|
3.
|
Комплексные числа. Производная. Комбинаторика и вероятность.
|
|
|
|
4.
|
Входная контрольная работа по типу ЕГЭ
|
|
|
|
|
МНОГОЧЛЕНЫ
|
|
10
|
|
5.
|
§1. Многочлены от одной переменной
|
|
|
|
6.
|
§1.Многочлены от одной переменной
|
|
|
|
7.
|
§1.Многочлены от одной переменной
|
|
|
|
8.
|
§2.Многочлены от нескольких переменных
|
|
|
|
9.
|
§2.Многочлены от нескольких переменных
|
|
|
|
10.
|
§2.Многочлены от нескольких переменных
|
|
|
|
11.
|
§3.Уравнения высших степеней
|
|
|
|
12.
|
§3.Уравнения высших степеней
|
|
|
|
13.
|
§3.Уравнения высших степеней
|
|
|
|
14.
|
Контрольная работа №1 «Многочлены»
|
|
|
|
|
ВЕКТОРЫ В ПРОСТРАНСТВЕ
|
|
6
|
|
15.
|
Понятия вектора в пространстве
|
|
|
|
16.
|
Сложение и вычитание векторов. Умножение вектора на число
|
|
|
|
17.
|
Сложение и вычитание векторов. Умножение вектора на число
|
|
|
|
18.
|
Компланарные векторы
|
|
|
|
19.
|
Компланарные векторы
|
|
|
|
20.
|
Зачет
|
|
|
|
|
СТЕПЕНИ И КОРНИ. СТЕПЕННЫЕ ФУНКЦИИ
|
|
24
|
|
21.
|
§4. Понятие корня п-й степени из действительного числа
|
|
|
|
22.
|
§4. Понятие корня п-й степени из действительного числа
|
|
|
|
23.
|
§5.Функции у=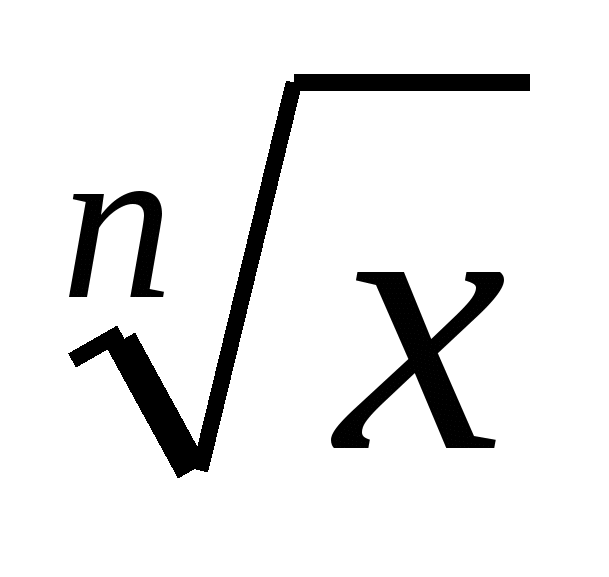 , их св-ва и графики , их св-ва и графики
|
|
|
|
24.
|
§5.Функции у=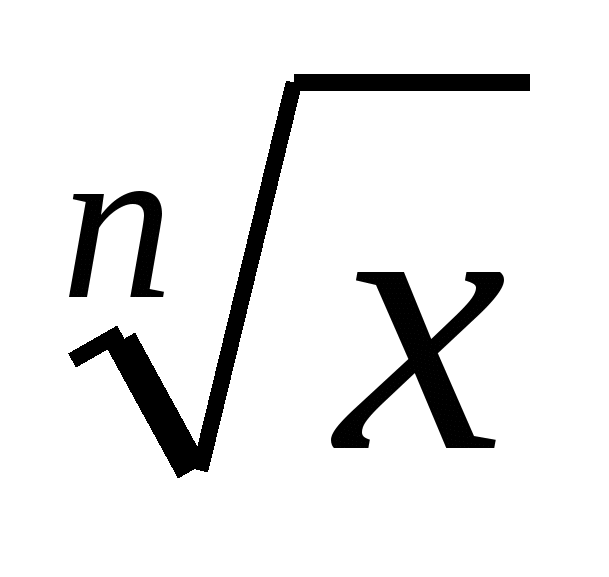 , их св-ва и графики , их св-ва и графики
|
|
|
|
25.
|
§5.Функции у=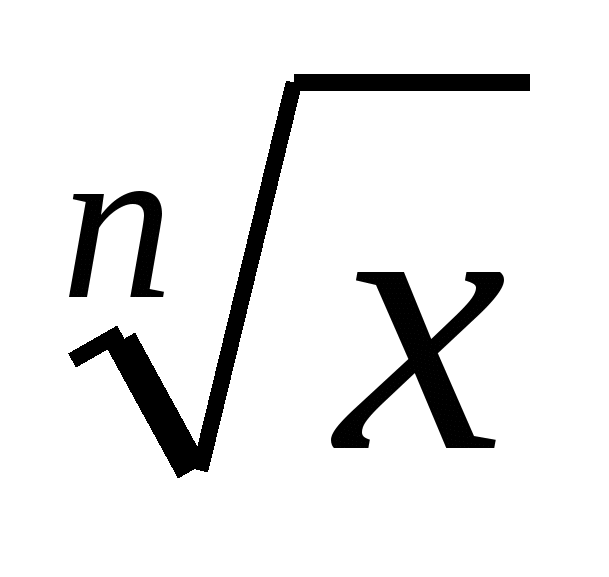 , их св-ва и графики , их св-ва и графики
|
|
|
|
26.
|
§6.Свойства корня п-й степени
|
|
|
|
27.
|
§6.Свойства корня п-й степени
|
|
|
|
28.
|
§6.Свойства корня п-й степени
|
|
|
|
29.
|
§7..Преобразование выражений содержащих радикалы
|
|
|
|
30.
|
§7..Преобразование выражений содержащих радикалы
|
|
|
|
31.
|
§7..Преобразование выражений содержащих радикалы
|
|
|
|
32.
|
§7..Преобразование выражений содержащих радикалы
|
|
|
|
33.
|
Контрольная работа «Степени и корни»
|
|
|
|
34.
|
§.8 Понятие степени с любым рациональным показателем
|
|
|
|
35.
|
§.8 Понятие степени с любым рациональным показателем
|
|
|
|
36.
|
§.8 Понятие степени с любым рациональным показателем
|
|
|
|
37.
|
§9.Степенные функции, их св-ва и графики
|
|
|
|
38.
|
§9.Степенные функции, их св-ва и графики
|
|
|
|
39.
|
§9.Степенные функции, их св-ва и графики
|
|
|
|
40.
|
§9.Степенные функции, их св-ва и графики
|
|
|
|
41.
|
§10.Извлечение корней из комплексных чисел
|
|
|
|
42.
|
§10.Извлечение корней из комплексных чисел
|
|
|
|
43.
|
Контрольная работа «Степенные функции»
|
|
|
|
|
Метод координат в пространстве
|
|
15
|
|
|
§ 1 Координаты точки и координаты вектора
|
|
6
|
|
44.
|
42.Прямоугольная система координат в пространстве
|
|
|
|
45.
|
43.Координаты вектора
|
|
|
|
46.
|
43.Координаты вектора
|
|
|
|
47.
|
44.Связь между координатами векторов и координатами точек
|
|
|
|
48.
|
45.Простейшие задачи в координатах
|
|
|
|
49.
|
45.Простейшие задачи в координатах
|
|
|
|
|
§ 2 Скалярное произведение векторов
|
|
7
|
|
50.
|
46.Угол между векторами
|
|
|
|
51.
|
47.Скалярное произведение векторов
|
|
|
|
52.
|
47.Скалярное произведение векторов
|
|
|
|
53.
|
48.Вычисление углов между прямыми и плоскостями
|
|
|
|
54.
|
Решение задач по теме «Скалярное произведение векторов»
|
|
|
|
55.
|
Контрольная работа по теме «Метод координат в пространстве»
|
|
|
|
56.
|
Зачет
|
|
|
|
|
Показательная и логарифмическая функции
|
|
31
|
|
57.
|
§11.Показательная функция, ее св-ва и график
|
|
|
|
58.
|
§11.Показательная функция, ее св-ва и график
|
|
|
|
59.
|
§11.Показательная функция, ее св-ва и график
|
|
|
|
60.
|
§12.Показательные уравнения
|
|
|
|
61.
|
§12.Показательные уравнения
|
|
|
|
62.
|
§12.Показательные уравнения
|
|
|
|
63.
|
§13.Показательные неравенства
|
|
|
|
64.
|
§13.Показательные неравенства
|
|
|
|
65.
|
§14.Понятие логарифма
|
|
|
|
66.
|
§14.Понятие логарифма
|
|
|
|
67.
|
§15.Логарифмическая функция, ее св-ва и график
|
|
|
|
68.
|
§15.Логарифмическая функция, ее св-ва и график
|
|
|
|
69.
|
§15.Логарифмическая функция, ее св-ва и график
|
|
|
|
70.
|
Контрольная работа «Показательная функция»
|
|
|
|
71.
|
§16.Св-ва логарифмов
|
|
|
| |
 Скачать 432.07 Kb.
Скачать 432.07 Kb.