Приемы активизации познавательной деятельности учащихся на уроках математики в 5-6 классах Актуальность проблемы
 Скачать 201.44 Kb. Скачать 201.44 Kb.
|
                                                                                                            Приемы активизации познавательной деятельности учащихся на уроках математики в 5-6 классах Приемы активизации познавательной деятельности учащихся на уроках математики в 5-6 классахАктуальность проблемы. На протяжении всей истории человечества математика является частью человеческой культуры, ключом к познанию окружающего мира, базой научно-технического прогресса, существенным элементом формирования личности. Каждый человек должен освоить навыки логического и алгоритмического мышления, научиться анализировать, отличать гипотезу от факта, понимать смысл поставленной задачи, схематизировать, отчётливо выражать свои мысли. С другой стороны, нужно развить воображение и интуицию, пространственное представление, способность предвидеть результат и предугадать путь решения. Всему этому можно и нужно учить на уроках математики. Математика может способствовать формированию мировоззрения и ориентации в информационной и компьютерной технологиях, необходимых ныне каждому. Одной из главных задач школы является повышение эффективности обучения за счёт преодоления неуспеваемости. В качестве реального факта необходимо признать, что достаточно большая часть школьников отличается объективным неприятием математики. Однако без математического образования современный человек обойтись не может в силу следующих причин: - математическое образование – это единственное прошедшее испытание временем средство интеллектуального развития в условиях неизбежного массового обучения; - элементы математики – неотъемлемая часть общей системы ориентации в окружающем мире. Практически каждому человеку приходится постоянно проводить элементарные подсчеты, делать оценки, прикидки, читать графики, осмысливать статистические данные и т. д.; - математика обладает колоссальным воспитательным потенциалом: воспитывается интеллектуальная честность, критичность мышления, способность к размышлениям и творчеству. Сложность заключается в создании привлекательного для учащихся курса математики. Возникает необходимость кропотливого поиска таких приёмов методики преподавания и организации учебного процесса, чтобы не заставлять насильно делать неинтересное, чтобы ученику «захотелось» понять и учить математику. Учение – это направленный и мотивированный процесс, поэтому задача учителя состоит в том, чтобы включить каждого ученика в деятельность, обеспечивающую формирование и развитие познавательных потребностей – познавательные мотивы. К тому же в современных условиях, важное значение приобрела проблема профессиональной подготовки специалистов, способных мыслить и действовать творчески, самостоятельно, нетрадиционно. Одной из главных задач школы является не только сообщение определённой суммы знаний учащимся, но и развитие у них познавательных интересов, творческого отношения к делу, стремления к самостоятельному «добыванию» и расширению знаний и умений, совершенствованию умения применять их в своей практической деятельности. Реализовывать данную задачу поможет отлаженная система работы учителя и учащихся. Работать над активизацией познавательной деятельности – это значит формировать положительное отношение школьников к учебной деятельности, развивать их стремление к более глубокому познанию изучаемых предметов. Для развития познавательных интересов необходимо выполнение следующих условий: - избегать в стиле преподавания будничности, монотонности, серости, бедности информации, отрыва от личного опыта ребёнка; - не допускать учебных перегрузок, переутомления и низкой плотности режима работы; - использовать содержание обучения как источник стимуляции познавательных интересов; - стимулировать познавательные интересы многообразием приемов занимательности (иллюстрацией, игрой, кроссвордами, задачами – шутками, занимательными упражнениями и т. д.); - специально изучать приемам умственной деятельности и учебной работы, использовать проблемно-поисковые методы обучения. Знания ученика будут прочными, если они приобретены не одной памятью, не заучены механически, а являются продуктом собственных размышлений и проб и закрепились в результате его собственной творческой деятельности над учебным материалом. Д. Пойа писал «математический опыт учащегося нельзя считать полным если он не имел случая решить задачу, изобретённую им самим». Одной из главных задач учителя является организация учебной деятельности таким образом, чтобы у учащихся сформировались потребности в осуществлении творческого преобразования учебного материала с целью овладения новыми знаниями. Работать над активизацией познавательной деятельности – это значит формировать положительное отношение школьников к учебной деятельности, развивать их стремление к более глубокому познанию изучаемых предметов, Основная задача учителя – повышение в структуре мотивации удельного веса внутренней мотивации учения. Высокая познавательная активность возможна только на интересном для ученика уроке, когда ему интересен предмет изучения. И наоборот «воспитать у детей глубокий интерес к знаниям и потребность в самообразовании – это значить пробудить познавательную активность и самостоятельность мысли, укрепить веру в свои силы». Любой педагог, пробуждая интерес к своему предмету , не просто осуществляет передачу опыта, но и укрепляет веру в свои силы каждого ребёнка независимо от его способностей. Следует развивать творческие возможности у слабых учеников, не давать остановиться в своём развитии более способным детям. Учить всех воспитывать у себя силу воли, твёрдый характер и целеустремлённость при решении сложных заданий. Всё это и есть воспитание творческой личности в самом широком и глубоком понимании этого слова. Но для создания глубокого интереса учащихся к предмету, для развития их познавательной активности необходим поиск дополнительных средств, стимулирующих развитие общей активности, самостоятельности, личной инициативы и творчества учащихся разного возраста. И учебник, и урок должны быть увлекательными. Интерес школьников к учению надо рассматривать как один из самых мощных факторов обучения. Математику надо рассматривать не как систему истин, которые надо заучивать, а как систему рассуждений, требующую творческого мышления. Умение заинтересовать математикой – дело не простое. Многое зависит от того, как поставить даже очевидный вопрос, и от того, как вовлечь всех учащихся в обсуждение сложившейся ситуации. Творческая активность учащихся, успех урока целиком зависит от методических приёмов, которые выбирает учитель. Обучение математике в школе вполне можно и нужно строить так, чтобы оно представлялось для учащегося серией маленьких открытий, по ступенькам которых ум ученика может подняться к высшим обобщениям. Организация активной познавательной деятельности на уроке математике.
Приёмы активизации познавательной деятельности учащихся. Умение заинтересовать математикой дело непростое. Многое зависит от того, как поставить даже очевидный вопрос, и от того, как привлечь всех учащихся в обсуждении сложившейся ситуации. Творческая активность учащихся, успех урока целиком зависит от методических приёмов, которые выбирает учитель. Как сформулировать интерес к предмету у ребёнка? Через самостоятельность и активность, через поисковую деятельность на уроке и дома, создание проблемной ситуации, разнообразие методов обучения, через новизну материала, эмоциональную окраску урока. О некоторых средствах повышения эффективности обучения и приёмах активизации познавательной деятельности учащихся пятых, шестых классов, которые используются мною, я хочу рассказать. Не всё представленное вашему вниманию является моим изобретением многое, есть результат перенятого опыта у коллег, а также из источников полезной информации. Создание на уроке учебной проблемной ситуации. Сообщить готовое быстрее чем открывать его вместе с учениками , но от прослушанного как известно через две недели в памяти остается только 20%. Важно сделать учащихся участниками научного поиска рассуждая вслух высказывая предложения обсуждая их доказывая истину. Учащихся включая деятельность, которая носит исследовательский характер. В реализации проблемного обучения существенную роль играет создания на уроке учебной проблемной ситуации. Это оправдывающий себя дидактический приём, с помощью которого учитель держит в постоянном напряжении одну из внутренних пружин процесса обучения детскую любознательность. Выдающийся немецкий педагог А. Дистервег убеждал, что развитие и образование ни одному человеку не могут быть даны или сообщены. Это можно достичь собственной деятельностью собственными силами собственным напряжением. Проводя урок по теме «Признаки делимости на 10, на5, на2», учитель на доске записывает числа: 1 289 565, 246 560, 24, 188 536, 1873 и предлагает ученикам найти среди этих чисел те, которые делятся на 10, на 5, на 2, не производя деления; написать несколько многозначных чисел, делимость которых на 10, на 5, на 2 они могут предугадать; попытаться найти признаки делимости чисел на 10, на 5, на 2. Высказать своё мнение: стоит ли этим заниматься? Разрешается обсуждение с соседом или в группе. После высказывания предположений ученики проверяют их непосредственным делением. Затем идёт сопоставление с учебником, и формулируются окончательные выводы. Например, при изучении темы 6 класса “Сложение дробей с разными знаменателями” в устный счёт, состоящий из примеров на сложение и вычитание дробей с одинаковыми знаменателями (“ситуация успеха”) включаем задание, где знаменатели разные. Происходит “заминка” (проблема), и начинают думать: “почему не получилось?”. Анализируем, сравниваем, обобщаем… Итог: верное решение и понимание – что делаем? как делаем? Зачем ? Учащиеся 6 класса получают домашнее задание: каждый измеряет, пользуясь ниткой и миллиметровой линейкой, длину С окружности и диаметр D какого-либо круглого тела и вычисляет отношение первого результата ко второму. Несколько учащихся вызываются к доске и вписывают в начерченную там таблицу результаты своих измерений. Можно поручить одному-двум учащимся, аккуратно начертить такую таблицу для всего класса и уже заполненную принести на урок. Изучая на уроке эту таблицу, учащиеся открывают закономерность: отношение длины окружности к ее диаметру остается почти постоянным. Учителю остается добавить: в математике доказано, что это отношение строго постоянно и может быть вычислено с любой точностью; до 0,01 равно 3,14. Каждый учащийся получает возможность оценить, насколько точно он провел измерения (сопоставляя это число со своим результатом). Уроки по темам «Нахождение дроби от числа» и «Нахождение числа по его дроби». Предложить ученикам следующие задачи.
Ученикам предлагается дополнить условие задачи. Одни советуют указать, сколько процентов составляет площадь, засеянная горохом; другие - указать, на сколько меньше эта площадь площади всего поля; третьи – выразить эту площадь в долях от всего поля. Учитель выбирает нужный вариант.
Ученики дополняют условие задачи. Рассматривается нахождение числа по его дроби. Такие проблемные ситуации можно создавать практически на каждом уроке математики и совместно с учащимися успешно с ними справляться. ПРАКТИЧИСКИЕ РАБОТЫ КАК СРЕДСТВО АКТИВИЗАЦИИ ПОЗНАВАТЕЛЬНОЙ ДЕЯТЕЛЬНОСТИ ШКОЛЬНИКОВ. Одним из средств активизации познавательной деятельности школьников является широкое использование их жизненного опыта. Большую роль в усвоении материала играют при этом практические работы. Часто дети запоминают только то, над чем потрудились их руки, если ученик что-то рисовал, чертил, вырезал или раскрашивал, это что-то само по себе становится опорой его памяти. Такой вид работы, как обучающее практическое занятие, является творческим для учащихся. Выполнение задания и обобщение результатов приводит их к новому математическому занятию. В этих условиях познавательная деятельность представляет собой самодвижение. В результате такой работы новые знания не поступают извне в виде информации, а являются внутренним продуктом практической деятельности самих учащихся. Приведу примеры. Практическая работа №1. Тема: Прямоугольный параллелепипед. У каждого на парте куб и прямоугольный параллелепипед. Задание: 1. измерьте длину, ширину и высоту прямоугольного параллелепипеда и куба. Данные занести в таблицу.
Вычислите по формулам объём, площадь, сумму длин рёбер прямоугольного параллелепипеда. Y = а · в · с; Y = S = 2 · (а · в + в · с + а · с); S = P = 4 · (а + в + с); P = Y = а3; Y = S = 6 · а2; S = P = 12 · а; P = 3. Заполните таблицу. 4. Сделайте вывод. Практическая работа №2.
Т О В К С Р А М На рисунке изображён прямоугольный______________________ Точка К – его__________________________________________ Отрезок АВ – его__________________________________________ Прямоугольник АВКМ – его_________________________________ 2. Обведите равные рёбра параллелепипеда одним цветом. Практическая работа № 3. Тема «0быкновенные дроби». У каждого ученика цветные карандаши и раздаточный материал. Задание. 1. Начертите квадрат со стороной 3 см. Разделите на 4 равные части. Закрасьте ¼ часть квадрата. 2. Начертите отрезок длиной 5 см. Обведите цветным карандашом 5/5 отрезка. 3. На рисунке изображена ⅓ часть веточки с одинаковыми листочками. Дорисуёте всю веточку.  Практическая работа №4. Тема: «Длина окружности». У каждого учащегося по три круга разного диаметра, кусочек нитки, линейка. Задание.
2. Найдите отношение длины окружности к диаметру для каждой окружности. С1/d1 = C2/d2 = C3/d3 =
Использование опорных схем на уроке. Велика роль опорных схем или карточек – информаторов в организации познавательной деятельности учащихся. Их лучше составлять вместе с учащимися на уроке в самом начале изучения темы, и можно пользоваться, пока тема не исчерпана. Помогают они и при повторении. Опорные схемы, карточки – информаторы уменьшают нагрузку на память, помогают преодолеть страх перед необходимостью изложить материал самостоятельно. Примеры:
на сколько равных частей разделили знаменатель сколько таких частей взяли числитель
  = =  = = 2 + 1 3. + - + = + ( - ) + - + = - ( - ) - - + Сложение отрицательных чисел. = - ( + ) Сложение чисел с разными знаками. По сторонам. Виды треугольников. равнобедренный равносторонний разносторонний По углам. прямоугольный тупоугольный остроугольный Другие приемы организации познавательной деятельности. Одной из основных задач преподавания курса математики в школе является формирование у учащихся сознательных и прочных вычислительных навыков. О наличии у учащихся вычислительной культуры можно судить по их умению производить устные и письменные вычисления, рационально организовывать ход вычислений, убеждать в правильности полученных результатов. Вычислительные навыки отличаются от умений тем, что выполняются почти бесконтрольно. Такая степень овладения умениями достигается в условиях их целенаправленного формирования. Поэтому большое внимание на уроках уделяю устному счёту, различным приёмам устной работы. Организация устных вычислений в методическом отношении представляет собой большую ценность. В ходе устного счёта развивается память, быстрота реакции, воспитывается умение сосредоточиться, инициатива учащихся, потребность к самоконтролю, повышается культура вычислений. А использование методов анализа и синтеза способствует развитию логического мышления учащихся. Использую следующие виды работ:
6,4 ? : 8 + 1,4 ∙ 3 - 5,1 Найдите правило нахождения чисел, помещённых в «голове». Заполните свободный кружок. 2. 44 25 63 47 20 74 84 16 3. Среди чисел, записанных в правой части, найдите значение каждой из сумм. Суммы Значения сумм 1693 + 789 132752 57854 + 789 2683 131963 + 789 58643 1894 + 789 2482 4. Напишите на корпусе каждой лодки такое число, чтобы равенство было верным. 7 ∙ 5 = 7 + 9 + = 9 ∙ 5 49 : 7 = 49 - 235 + 245 = ∙ 10 37 + 59 = 3 ∙ 201 – 199 = 96 : 5. Зашифрованное слово: Выполните вычисления. Из букв, соответствующих найденным ответам, составьте слово. 1,6 + 4; 10,5:5 ; 3,6 0,3; 7,4 + 3,7 1,6:8 ; 2,6 5 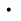 Н Ф М И У В З 13 0,018 0,084 0,3 0,008 1,08 10,8 Е П А Т Р С К 11,1 2 10,11 2,1 1,4 5,6 1,8 6. Выполните вычисления по схеме. 15 4 12 3 68 72 - - : 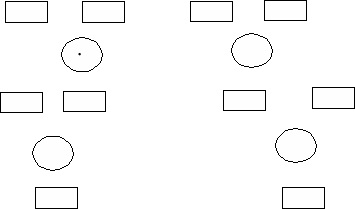 И 1 Я 0,3 В кружки впишите буквы, соответствующие найденным ответам. 3,6 ∙ 3 = 0,25 ∙ 4 = 0,05 ∙ 4 = 0,004 ∙ 6 = 2,6 ∙ 5 = 0,125 ∙ 8 = 0,02 ∙ 15 = Н 1,3 К 10,8 А 0,024 Л 1,3 Г 0,2 Оживляет урок и использование материала из истории математики. Можно это делать учителю, можно давать задание детям. Не надо тратить на это много времени, но 1 – 3 минуты, потраченные на исторические данные, вызывают интерес и находят в детских душах живой отклик. В настоящее время происходит активное внедрение информационных и коммуникационных технологий во все сферы жизнедеятельности человека. Если раньше использование вычислительной техники в школах сводилось лишь к обучению информатике, то сейчас функции компьютера превратили его в незаменимого помощника для учителя – предметника, особенно естественно – научного цикла. Одним из свойств использования компьютера на уроке является создание благоприятной обстановки для обучения. Компьютер вызывает интерес у учащихся. Он снимает психологический барьер между учеником и учителем, вызванный объективными и субъективными причинами. Эти причины тормозят развитие творческих способностей учащихся, процесс обмена информацией. Использование компьютера на уроке существенно меняет ситуацию. Можно выделить следующие способы применения компьютерной техники на уроке математики : 1) подготовка печатных раздаточных материалов (самостоятельные, контрольные работы, дидактические карточки для индивидуальной работы); 2) мультимедийное сопровождение объяснения нового материала (презентации, учебные видеоролики). 3). Контроль знаний. При контроле используются тесты. Возможны две формы организации тестов, которые условно можно назвать «выбери ответ из предлагаемых вариантов» и «напиши правильный ответ». Литература 1.С.В. Кульневич, Т.П. Лакоценина. « Современный урок ,часть III. Проблемные уроки» . Волгоград: Учитель, 2006. 3. С.Г. Манвелов. « Конструирование современного урока математики». Москва: Просвещение, 2002. 4. Н.И. Зильберберг. « Урок математики. Подготовка и проведение». М: Просвещение, 1995. 8. Газета « Математика в школе», статья О. Петровой «Мотивация учения». 2004, №38. 9. Журнал « Математика в школе», статья С. Шестакова «О школьном математическом образовании». 2003, №36 10. Виленкин Н. Я. Математика – 6. Москва: Мнемозина, 2015. 11. Виленкин Н. Я. Математика – 5 Москва: Мнемозина, 2015. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||