"Уравнение с одной переменной". 9-й класс

Скачать 69.63 Kb. Название "Уравнение с одной переменной". 9-й класс Дата 10.02.2016 Размер 69.63 Kb. Тип Урок

Тема урока: "Уравнение с одной переменной". 9-й класс Используемая технология: Блочно-модульное обучение. По учебнику Макарычев Ю.Н. Цели: Образовательные: Сформировать понятие и закрепить знания учащихся по теме “Уравнения с одной переменной”; Умения составлять алгоритм решения уравнения; Закрепить умения и навыки решать уравнения высших степеней с использованием разных приемов, в нестандартных ситуациях. Развивающие: Развивать умения пользоваться опорным конспектом и вспомогательной литературой для постановки задачи и ее выполнения в ходе решения; Развивать внимательность, собранность и аккуратность; Развивать умения работать самостоятельно и в микро группах, ставить перед собой цель и делать выводы, выполнять безошибочно необходимые арифметические вычисления Воспитывающие: Чувство ответственности; Умение работать в микро группе; Культура труда, аккуратность. На этом уроке учащимся предлагается самостоятельно выполнить работу с целью определения уровня владения новым материалом. Каждому выдается разработка модуля урока, учащийся сам выбирает темп работы и по окончанию урока (2 часа) получает отметку. Комментарий: У учителя разработка с ответами, учащимся же выдается без ответов. Разработка модуля урока по теме: ” Решение уравнений высших степеней”, 9 класс. ДЛЯ УЧИТЕЛЯ Для успешного освоения данной темы: На ”3” нужно выполнить таблицы №1,№2,№3 На “4” нужно выполнить таблицы №1- 4 На “5” нужно выполнить все задания. Желаю УДАЧИ всем!!! Блок №1. Решить различные уравнения уже известными способами. Цель: Закрепить знания и умения, полученные ранее. Виды уравнений: № Название уравнения Общий вид пример 1. Биквадратное ах4+ вх2 + с = 0 замена х2=t обратная замена переменных 3х4- 5х2 + 8=0 замена х2 = t 3 t2- 5 t +8=0 2. Уравнение, сводящееся к квадратному с помощью замены выражения.   (х2- 3х)2 + 5(х2- 3х) = 2 замена (х2- 3х) = а а2 + 5а = 2 а2 + 5а - 2 = 0 3. Уравнение, решая которое используем метод группировки слагаемых. Прием группировки 3(х-5) –х(х-5)=(х-5)(3-х) 3х-15-х2+5х=0 3(х-5) + х(-х+5)=0 3(х-5) – х(х-5)=0 (х-5)(3-х)=0 х - 5=0 или 3 - х=0 Блок №1. Решить различные уравнения уже известными способами. Таблица №1 служит разминкой для дальнейшего решения уравнений более высокой степени. Следует решить два уравнения из таблицы, проверить результат и если вы успешно справились, то перейти к следующему заданию. ТАБЛИЦА №1 1. (х+5)(3х-6) = 0 2. х2- 6х = 0 3. (8х –1)2- х(64х + 1) = 12 4. х –5 + 4х-1 = 1 5. 0.5х2- х2 = 0 Блок №2. Решить уравнения, сделав замену переменных. Цель: Закрепить способ решения уравнений, используя замену переменных. Пример- образец №1. Решить уравнение (х2+2х)2 - 2(х2+ 2х) = 3 Решение: Запишем равносильное данному уравнение (х2+ 2х)2 – (х2+ 2х) –3 =0, сделаем замену переменных, выражения в скобках одинаковые, поэтому можно записать: Пусть х2 + 2х =у, тогда Перепишем получившееся уравнение и решим его. у2 - 2у – 3= 0 Д= в2- 4ас= (-2)2- 4·1·(-3)= 16 у= 3, у= -1 Вернемся теперь к переменной х, сделаем обратную замену и решим два уранения. Обратная замена: 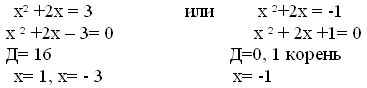Ответ: 1, -3, -1. ТАБЛИЦА №2 Вариант 1 Вариант 2 1. (х2 +6х)2 –5 (х2 +6х) = 24 2. (х2+2)2– (х2+2) = 12 1. (х2 –5)2 –5 (х2 –5) – 36 =0 2. (х2 –4х)2 + 9(х2-4х) = - 20 Блок №3. Решение биквадратных уравнений. Цель: Закрепить способ решения биквадратных уравнений. Уравнение вида ах4+вх2+с=0, где а,в,с – числа, х – неизвестная переменная называется биквадратным уравнением. Решение биквадратного уравнения с помощью замены переменной сводится к решению квадратного уравнения. Пример-образец №2 Решить биквадратное уравнение х4 – 5х2 +4 = 0 Решение: х4 –5х2 +4 =0, биквадратное уравнение, сделаем замену переменной и решим получившееся квадратное уравнение. Пусть х2= t , тогда t2-5t +4 = 0 D= 9 t= 4, t= 1 Оба корня положительные, поэтому удовлетворяют условию t >= 0. Обратная замена: Ответ: ± 2, ± 1. ТАБЛИЦА №3 Вариант 1 Вариант 2 1. х4 – 2х2- 3 =0 2. 5у4 – 5у2 + 2 = 0 3. х4 – 4х2 + 4 = 0 1. х4 – 5х2 - 36 = 0 2. у4 – 6у2 + 8 = 0 3. 2х4 – 9х2 + 4 = 0 Блок №4. Решить уравнения высшей степени. Цель: Закрепить разные способы решения уравнений высших степеней. Если ребята вы добрались до 4 блока, поздравляю вас, вы делаете успехи. Сейчас вам предстоит самостоятельно выбирать способ решения, переменную, которую нужно заменить. Таблица №4 Вариант 1 Вариант 2 1. (х2 +2х)(х2 +2х +2) = 3 2. х4 – 9х2 + 18 =0 3. (х2 –х-16)(х2-х+2) =88 1. (х2 +х)(х2 +х - 5) = 84 2. х4 – 20х2 +100 =0 3. (2х2 +7х –8)(2х2 +7х – 3) –6 =0 Блок №5. Указания учителя. Молодцы!!! Вы ребята освоили решение уравнений высших степеней. Целью дальнейшей вашей работы является применение своих знаний и умений в более сложных ситуациях. Таблица №5 1. (х2 –1)(х2 +1) – 4(х2 – 11) = 0 2. х5 + х4 – 6х2 – 6х2 + 5х +5 = 0 3. При каких с не имеет корней уравнение х4 – 12х2 +с = 0 Указания учителя: В случае затруднений воспользуйтесь подсказками, данными ниже. Подсказки. 1. Воспользуйтесь формулой (а-в)(а+в)=а2-в2, преобразуйте данное уравнение в биквадратное. 2. Сгруппируйте первое слагаемое со вторым, третье с четвертым и пятое с шестым, примените способ группировки и разложите на множители. 3. Сделайте замену и запишите условие, при котором уравнение не имеет корней, решите получившееся неравенство. ОТВЕТЫ: (только у учителя) ОТВЕТЫ № таблицы № задания вариант I II     1 1 - 5; 2.   2 0, -v6, v6. 3 - 11/17 4 23/11 5 0; 2. 2 1 - 3±v6; - 3 ± v17 ±2, ± 1. 2 ±v2 2 3 1 ±v3 ± 3 2 Нет корней ±v2, ± 2 3 ± v2 ± 0.5; ± 2. 4 1 - 1, 3. - 3, 4. 2 ±v3, ± v6. ±v10 3 - 4, 5. -4,5; 1; (-7± v65)· 0,25 5 1 Нет корней   2 ±1, ±v5 3 с > 36