Математические карты
Взаимное расположение прямых
пересекаются параллельны скрещиваются
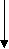 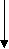 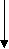
способ задания способ задания признак скрещивающихся
плоскостей плоскостей прямых
Взаимное расположение прямой и плоскости
 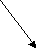

.прямая пересекает плоскость прямая не пересекает плоскость
угол между признак и свойства признак и свойства
прямой и перпендикулярности параллельности
плоскостью прямой и плоскости прямой и плоскости
3. Взаимное расположение плоскостей
совпадают параллельны пересекаются
признаки и свойства признаки и свойства двугранный
параллельности плоскостей перпендикулярности (многогранный)
плоскостей угол
Глава2.Практические разработки по теме «Взаимное расположение прямой и плоскости в пространстве».
§1. Разработки уроков.
1. «Построение сечений многогранников на основе аксиоматики.»
10 класс ( по учебнику Атанасяна Л. С.) |

|
|
 
| Урок 1. '' Круглый стол". ( 2 часа ) Урок обобщения и систематизации знаний учащихся по геометрии в 1О классе.
Необходимость в уроках обобщения и систематизации знаний по геометрии в старших классах вызвано, с одной стороны, психолого-дидактическими особенностями деятельности учащихся, а с другой - структурой программы учебного курса стереометрии.
Особенность человеческого мышления такова, что даже простейшее восприятие и запоминание требуют неоднократного обращения к материалу. Начальные темы стереометрии изучаются длительное время, поэтому процесс забывания неизбежен. Следовательно, программой необходимо предусмотреть уроки тематического повторения, работающие на перспективу применения этих знаний в новой ситуации.
Главная цель таких уроков - в углублении, обобщении, систематизации, закреплении полученных знаний и развитии их в перспективе. Обобщающее повторение начал стереометрии имеет особое значение, т.к. является фундаментом для решения задач на построение сечений, нахождение их площадей, нахождение площадей поверхности и объемов и др. Для того, чтобы избежать однообразия и активизировать самостоятельную деятельность учащихся, необходимо расширить знания учащихся. Поэтому учебник уже не может быть единственным источником знаний, старшеклассники должны уметь работать с дополнительной литературой. Одним из видов домашнего задания на повторение является написание рефератов или выступлений. Данные рефераты и выступления предлагаются нескольким учащимся и готовятся они под руководством учителя.
Каковы бы ни были формы урока, все они направлены на достижение следующих целей:
Цели уроков методической разработки. 1.Дидактические.
а) Наилучший способ обучения учащихся, дающий им сознательные и прочные знания и обеспечивавший одновременное их умственное развитие заключается в том, что перед учащимися ставятся последовательно одна за другой посильные теоретические практические задачи, решение которые дает им новые знания.
б) Обучение на немногочисленных, но хорошо подобранных задачах решаемых школьниками в основном самостоятельно, способствует вовлечению их в творческую исследовательскую работу, последовательно проводя через этапы научного поиска.
в) С помощью задач, последовательно связанных друг с другом, можно ознакомить учеников даже с довольно сложными математическими теориями.
г) Усвоение материала курса через последовательное решение учебных задач происходит в едином процессе приобретения новых знаний и их немедленного применения, что способствует развитию познавательной самостоятельности и творческой активности учащихся.
2. Общекультурные и научные (геометрические).
К ним относится развитие вербально-логического, наглядно-действенного (практического), наглядно-образного, пространственного, визуального и др. типов мышления, развитие свойств интеллекта:
а) геометрическая интуиция на образы, свойства, методы построения.
б) пространственное мышление (одно-, двух-, трех мерное евклидовое пространство), пространственные абстракции, их общность, анализ и синтез геометрических образов, пространственное воображение.
в) логическое мышление (владение правилами логического вывода и построения, владение разными методами геометрии)
г) способность к конструктивно-геометрической деятельности.
д) владение символическим языком геометрии.
3. Воспитательные.
Аккуратность, коллективизм, ответственность за себя и товарищей, дружбу, любовь к предмету и др.
4. Прикладные.
Умение анализировать задачу, работать с учебником, применять свои знания в новой ситуации.
ТЕМЫ выступлений для урока
1. Аксиомы стереометрии (таблицы остаются учащимся для работы).
А 1. Через любые две точки пространства проходит единственная прямая.
А 2. Через любые три точки пространства, не лежащие на одной прямой, проходит единственная плоскость.
А 3. Если две плоскости имеют общую точку, то они пересекаются по прямой.
Аксиома
|
Чертеж
|
Запись
|
А1
|
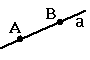
|
А,В 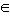 а, а - единственная прямая а, а - единственная прямая
|
А2
|

|
А, В, С  одной прямой. А, В, С одной прямой. А, В, С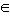  , ,  - единственная плоскость. - единственная плоскость.
|
А3
|
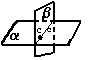
|
с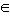  ; ;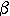
  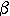 =с, С =с, С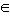 с. с.
|
В ходе беседы выделяются существенные моменты теории:
а) разъяснить содержание аксиом и иллюстрировать на модели;
б) чтение учащимися текста аксиом;
в) выполнение чертежа;
г) запись содержания с помощью символов.
2. Следствия из аксиом стереометрии.
|
Чертеж.
|
Формулировка.
|
Сл.1
|

|
Если две точки прямой принадлежат плоскости, то и вся прямая принадлежит этой плоскости.
|
Сл.2
|

|
Через прямую и не лежащую на ней точку можно провести плоскость и притом только одну.
|
Сл.3.
|

|
Через две пересекающиеся прямые можно провести плоскость и притом только одну.
|
В заключение предлагается схема логического строения геометрии (заготовленная заранее):
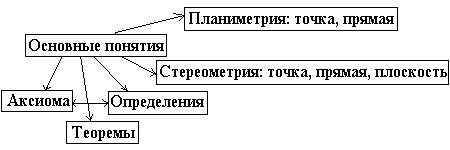
3. а) Взаимное расположение в пространстве двух прямых.
б) Взаимное расположение в пространстве прямой и плоскости.
в) Взаимное расположение в пространстве двух плоскостей.
г) Свойства, связывающие понятие параллельности двух плоскостей с понятием параллельности двух прямых.
Теорема. Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны.
 
Теорема (признак). Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны.
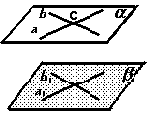 
4. Способы задания плоскостей.
Способы задания плоскостей
|
Рисунок
|
|
I. По трем точкам
|
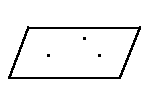
|
A2
|
2. По прямой и непринадлежащей ей точке.
|

|
Cл 2
|
3. По двум пересекающимся прямым.
|
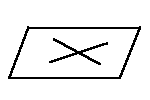
|
Cл 3
|
4. По двум параллельным прямым.
|

|
определение параллельных прямых
|
5. Используя полученные знания, применим их к построению сечений многогранников на основе аксиоматики:
Примеры и их решение приводят учащиеся (под руководством учителя).
N1. Построить сечение, определенное точками K, L, M.

N2. Построить сечение, определяемое параллельными прямыми АА1 и CC1.
 AA1//CC1 AA1//CC1
N3. АС1 и А1С. АС1  А1С. А1С.

N4. Построить сечение по прямой и точке: BC и М.

6. Построение сечений с использованием свойств параллельных плоскостей.
N1. Определите вид и найдите периметр сечения куба АВСДА1В1С1Д1 плоскостью, проходящей через ребро А1Д1 и середину ребра ВВ1, если длина ребра куба равна 8 см.
 P=16+8 P=16+8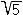 =8(2+ =8(2+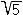 )см )см
N2. Определите вид и найдите периметр сечения куба АВСДА1В1С1Д1 плоскостью, проходящей через точки А, Д и середину ребра СС1, если длина ребра куба равна 4 см.
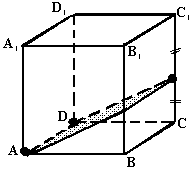 P=8+4 P=8+4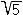 =4(2+ =4(2+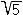 )см )см
N3. Определите вид сечения (и постройте его) куба АВСДА1В1С1Д1 плоскостью, проходящей через точку М 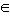 В1С1 и диагональ нижнего основания. В1С1 и диагональ нижнего основания.

7.
N1. Построить сечение правильной призмы плоскостью, проходящей через ребро АВ и середину ребра В1С1.
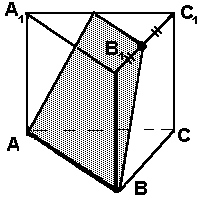
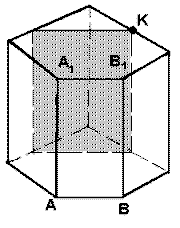
N2. Построить сечение пирамиды плоскостью, проходящей через точку К и параллельно плоскости основания пирамиды.

N3. Построить сечение призмы плоскостью, проходящей через точку К и параллельно плоскости грани АВВ1А1.
Урок 2. Лабораторная работа. (1 час).
В любой деятельности, в частности в учебной, выделяют две стороны: внешнюю - предметную и внутреннюю - психологическую. Успешное усвоение материала в любой области знания возможно, если первичной является внешняя деятельность, которая переходит во внутреннюю в результате преобразования внешних действий предметной учебной деятельности во внутренние субъективные характеристики ученика, его сознание. Такой процесс психологии называют интериоризацией. Это очень важное положение для изучения стереометрии в 10-11 кл. Для решения этой проблемы используется метод лабораторных работ.
Проведение лабораторных работ позволяет привлечь внимание учащихся к математике, сформировать интерес к ней. Форма проведения лабораторных работ отвечает индивидуальным особенностям обучения учащихся, способствует активизации их математической деятельности. Лабораторная работа проводится на два варианта (В-I, В-2).
N1. Постройте сечение куба по трем точкам, расположенным так, как
а) показано на рисунке:
В-1
|
|
В-2
|

|
|
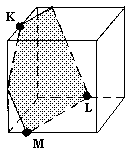
|
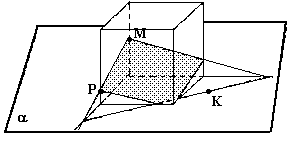
б) Построить сечение параллелепипеда плоскостью, проходящей через точки М, Р, К.
В-1
|
|
В-2
|
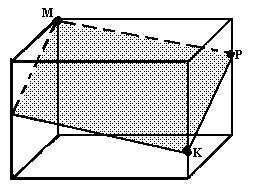
|
|

| N2. (Задача на использование свойств параллельности прямой и плоскости).
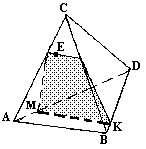
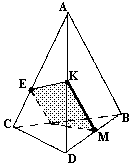
На рисунках изображены пирамиды. Постойте сечения этих пирамид плоскостью, проходящей через прямую МК и точку Е, зная, что МК||АВ, точка Е принадлежит плоскости (АВС). При построении используйте линейку и угольник.
a)
б)
N3. (Задача на использование свойств параллельных плоскостей).
В-1
Дан куб АВСДА1В1С1Д1. Докажите, что сечение куба плоскостью А1С1К, где точка К - середина ДС - трапеция.
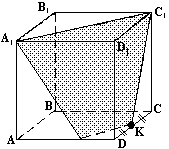
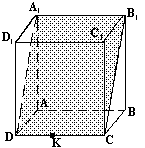
Решение: МК||А1С1, потому что (А1Д1С1) параллельна (АДС), а МК и А1С1 - линии пересечения этих плоскостей. МК||А1С1, А1М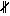 С1К, МК С1К, МК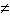 А1С1, значит МА1С1К - трапеция. А1С1, значит МА1С1К - трапеция.
В-2
Дан куб АВСДА1В1С1Д1. Докажите, что сечение куба плоскостью А1В1К - параллелограмм.
Решение: (АА1В1)||(ДД1С), то А1В1||ДС и А1В1=ДС. (АА1Д1)||(ВВ1С1), то А1Д||В1С, значит А1В1СД - параллелограмм.
N4. Постороить сечение многогранника плоскостью, проходящей через точки
М, Р, К, если К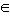  . .
В-1
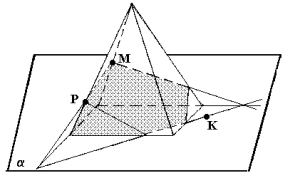
В-2
N5. Творческое задание.
Составить две задачи на построение сечений многогранников с использованием полученных знаний.
Решение задач лабораторной работы должно сопровождаться работой учащихся на моделях, изготовленных из спиц, спичек, пластилина или пенопласта. Учащиеся должны изготовить сечения из картона и использовать его при выполнении чертежа на бумаге. Такой поиск решения (руками) помогает при построении сечения.
|

|
2. «Взаимное расположение плоскостей. Параллельность плоскостей» (по учебнику Е. В. Потоскуева).
Цели урока:
- рассмотреть возможные случаи взаимного расположения плоскостей; изучить определение свойства и признаки параллельности плоскостей , применить их при решении простейших задач;
-развить познавательный интерес к предмету, творческое мышление, умение логически мыслить, обобщать, делать выводы;
-воспитание чувства ответственности и коллективизма, умение выслушать других и умение отстаивать свою точку зрения, уважая при этом другие мнения.
Оборудование: компьютер (проектор), стереометрический ящик, модель куба.
Дидактический материал: мультимедийные презентации.
Тип урока: изучение нового материала.
Формы работы на уроке: фронтальная, групповая, индивидуальная, работа в парах.
Ход урока
Вначале урока звучит музыка, на фоне которой идет презентация эпиграфа урока

Актуализация знаний.
Вопросы к классу.
С каких это «тёмных понятий» мы начинали раздел геометрии – стереометрию? (точка , прямая , плоскость , расстояние )Учитель их выписывает на откидную доску.
Как постепенно от урока к уроку проливался свет на эти темные понятия? (вначале изучались аксиомы , в которых давалось описание и основные свойства этих понятий , являющихся основополагающими в стереометрии ;
затем начали изучать связи между этими понятиями, опираясь на аксиомы).
Взаимное расположение каких объектов мы изучили?
( точка и прямая – используя аксиому о точке и прямой – есть точки принадлежащие прямой, есть ей не принадлежащие;
точка и плоскость - используя аксиому о точке и плоскости - есть точки принадлежащие плоскости, есть точки ей не принадлежащие;
взаимное расположение прямых – аксиома о прямой проходящей через две точки (через две точки проходит единственная прямая ) : две прямые имеют две общие точки – совпадают, одну общую точку – пересекаются, нет общих точек – параллельны или скрещиваются ;
взаимное расположение прямой и плоскости - аксиома о прямой и плоскости : прямая и плоскость имеют две общие точки – прямая лежит в плоскости, одна общая точка – прямая пересекает плоскость, нет общих точек - параллельны) .
Взаимное расположение, каких объектов осталось рассмотреть? (Плоскостей)
Сформулируйте мне тему сегодняшнего урока.
На доске записывается тема урока под диктовку учащихся:
«Взаимное расположение различных плоскостей»
.
Изучение нового материала
Вопросы к классу.
Каким может быть взаимное расположение плоскостей?
Чтобы аргументировать свои предположения, вспомните аксиому, в которой говорится о взаимном расположении плоскостей. (Аксиома пересечения плоскостей – две плоскости, имеющие одну общую точку, имеют общую прямую).
Исходя из этой аксиомы, скажите, каким может быть взаимное расположение различных плоскостей? (Плоскости имеют одну общую точку – пересекаются, и не имеют общих точек - не пересекаются.
Идёт показ слайда о взаимном расположении различных плоскостей до «не имеют общих точек»
Как вы думаете, как плоскости будут располагаться, если они не имеют общих точек? (параллельны).
Выполняя графическую работу дома, вы уже изображали параллельные плоскости и пересекающиеся.
Заканчивается показ слайда «Взаимное расположение различных плоскостей».
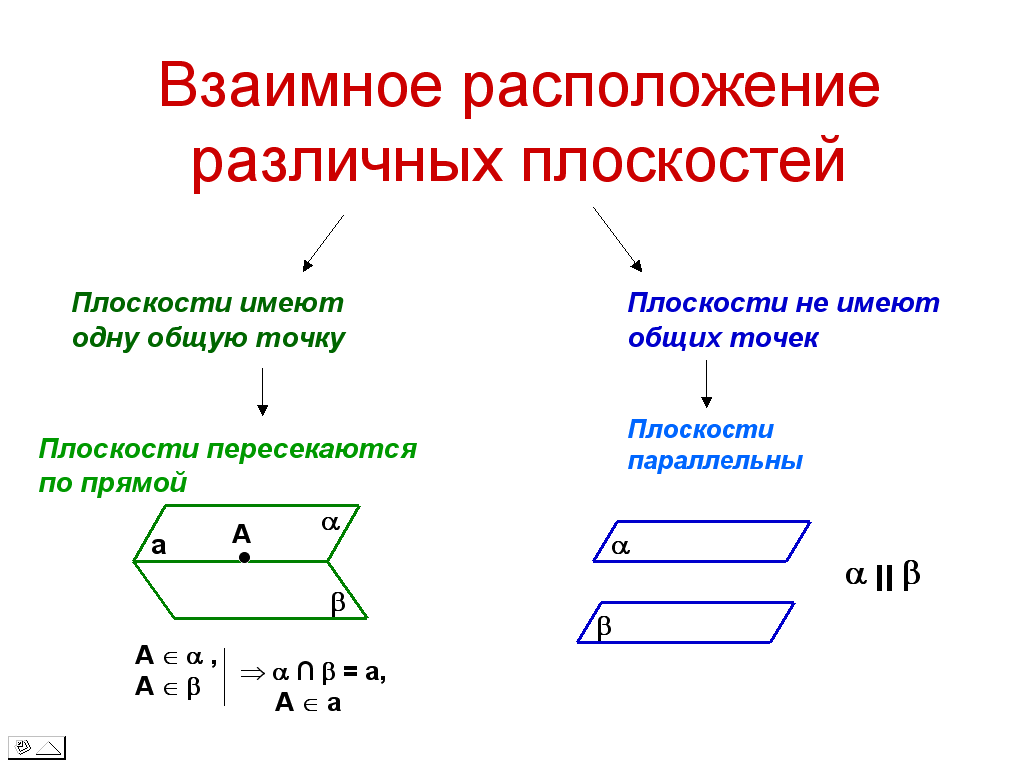
Делаем вывод: плоскости могут пересекаться или быть параллельными. Далее надо более подробно изучить эти расположения.
Какое взаимное расположение будем изучать первым? (параллельность).
Почему? (так как с параллельности начинали изучать взаимное расположение прямой и плоскости).
Уточните тему урока.
На доске записывается тема «Параллельность плоскостей» под диктовку учеников.
По какому плану будем изучать эту тему? (По такому же, как и взаимное расположение прямой и плоскости, т. е. определение, признак, построение, свойства)
На доске записывается план изучения темы (определение, построение, признак, свойства).
Дайте определение параллельности двух плоскостей.
Приведите примеры параллельных плоскостей из окружающей действительности. Будут ли указанные плоскости параллельными?
Существуют ли в природе параллельные плоскости? Может это только нам кажется, что есть параллельные плоскости?
Если мы сможем построить плоскость, параллельную данной, то тогда сможем утвердительно ответить на этот вопрос.
Следующим вопросом будет построение плоскости параллельной данной и проходящей через данную точку. Как это можно сделать?
Используя планшет, постройте плоскость, параллельную плоскости планшета, для этого вспомните способы задания плоскостей.
Идет практическая работа в парах по построению плоскости параллельной плоскости планшета , проходящая через конкретную точку и вырабатывается алгоритм по ее построению .
А
a
лгоритм
Ч  |
 Скачать 495.27 Kb.
Скачать 495.27 Kb.











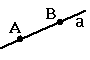






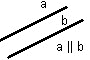















 AA1//CC1
AA1//CC1

 P=16+8
P=16+8 P=8+4
P=8+4