Методическая разработка по теме: «Методика изучения темы: «Взаимное расположение прямых и плоскостей в пространстве»
 Скачать 495.27 Kb. Скачать 495.27 Kb.
|
Отрезок ВМ перпендикулярен плоскости треугольника АВС. Докажите что:а) высота треугольника АМС и АВС пересекаются в точке на прямой АС;б) углы АСВ и АСМ либо оба – острые, либо оба – прямые, либо оба – тупые.№ 8 В правильном тетраэдре РАВС с ребром, равным 2, точка O – центр основания АВС. Найдите расстояние от точки O до плоскости грани РВС. № 9 РАВС – правильный тетраэдр с основанием АВС;А1- середина ребра АР;В1- середина ребра ВР;С1- середина ребра СР. а) Постройте сечение тетраэдра плоскостью СВА1. б) Докажите, что АР перпендикулярно плоскости ВСА1. в) Найдите площадь треугольника ВСА1, если ребро тетраэдра равно 2. № 10 ABCDA1B1C1D1 - куб. Найдите угол между плоскостью А1СС1 и прямой а, если прямая а образует с плоскостью АСВ1 угол 450. № 11 О - точка пересечения медиан правильного треугольника АВС. МО- перпендикуляр к плоскости АВС; МА = АВ = а; К – середина ВС; Р – точка пересечения медиан треугольника МВС. Заполните таблицу:
№ 12 В кубе ABCDA1B1C1D1 точка М – середина В1С1, точка F – середина D1C1, точка К – середина DC, O – точка пересечения диагоналей квадрата ABCD. Заполните таблицу:
№ 13 Докажите, что скрещивающиеся ребра правильного тетраэдра перпендикулярны. № 14 Докажите, что диагональ AC1 куба ABCDA1B1C1D1 перпендикулярна плоскости CB1D1. № 15 Через центры граней правильного тетраэдра проведены прямые, перпендикулярные плоскостям этих граней. Каково взаимное положение этих прямых? № 16 Ребра АВ и СР , АР и ВС тетраэдра РАВС взаимно перпендикулярны . Докажите , что ребра АС и ВР также взаимно перпендикулярны № 17 В тетраэдре РАВС плоские углы АРВ, ВРС и СРА прямые. Докажите , что ортогональной проекцией вершины Р на плоскость АВС является точка пересечения высот (ортоцентр) треугольника АВС № 18 В правильном тетраэдре РАВС опустите перпендикуляры на плоскость грани ВСР из следующих точек : а) Е – середина ребра АВ ; б) К – середины ребра АР ; в) Н – середины медианы РМ грани АРС. № 19 В кубе АВСDA1B1C1D1 с ребром а найдите расстояние от центра грани CDD1C1 до плоскости AB1C. №20 В кубе ABCDA1B1C1D1 точки E, Fи M – середины ребёр соответственно A1B1, B1C1 и BB1. Докажите, что прямая BD1 перпендикулярна плоскости EFM. № 20 В кубе ABCDA1B1C1D1 с ребром 2 точка М – середина ребра В1С1. а) Через точку М проведите прямую, перпендикулярную плоскости В1С1D1 б) Найдите длину отрезка этой прямой внутри куба. в) Найдите отношение, в котором плоскость B1CD1 делит данный отрезок. № 22 Дан куб ABCDA1B1C1D1. Точка K – середина ребра АВ, точка М – середина ребра ВС. Опустите перпендикуляры из точки А1 на следующие прямые: а) В1К и В1М; б) BD и KM; в) С1В и С1М. № 23 На грани ABCD куба ABCDA1B1C1D1 найдите все такие точки К, что прямая D1K образует с плоскостью ABC угол 45. Определите длину линии, образованной этими точками, если ребро куба равно 4. №24 На грани CDD1C1 куба ABCDA1B1C1D1 найдите такую точку K, что углы, образованные прямыми BK B1K с плоскостью CDD1, равны 45. Определите расстояние от этой точки до плоскости ABC, если ребро куба равно 2. §3. Презентации основных теорем по теме «Взаимное расположение прямых и плоскостей в пространстве».  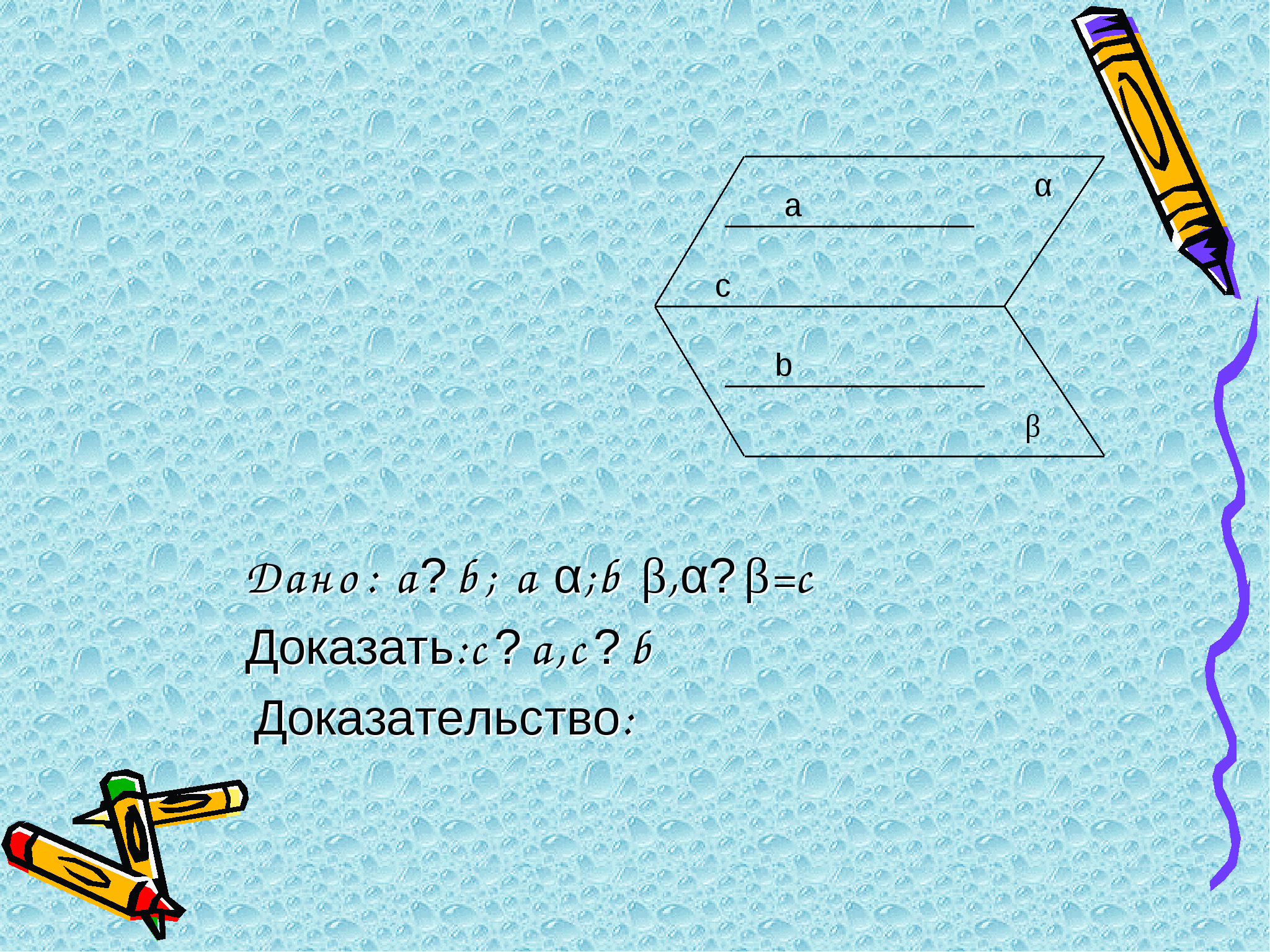 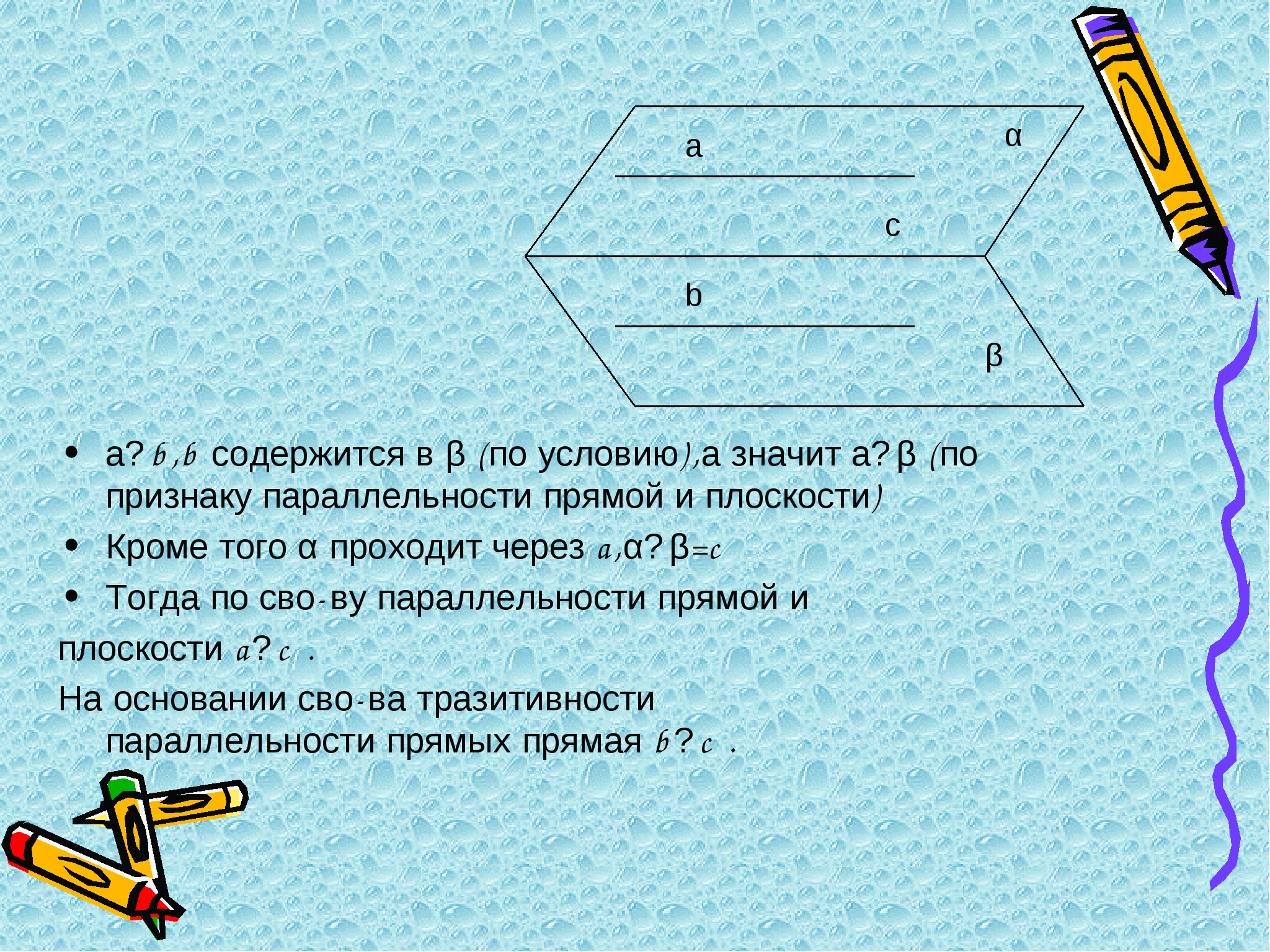              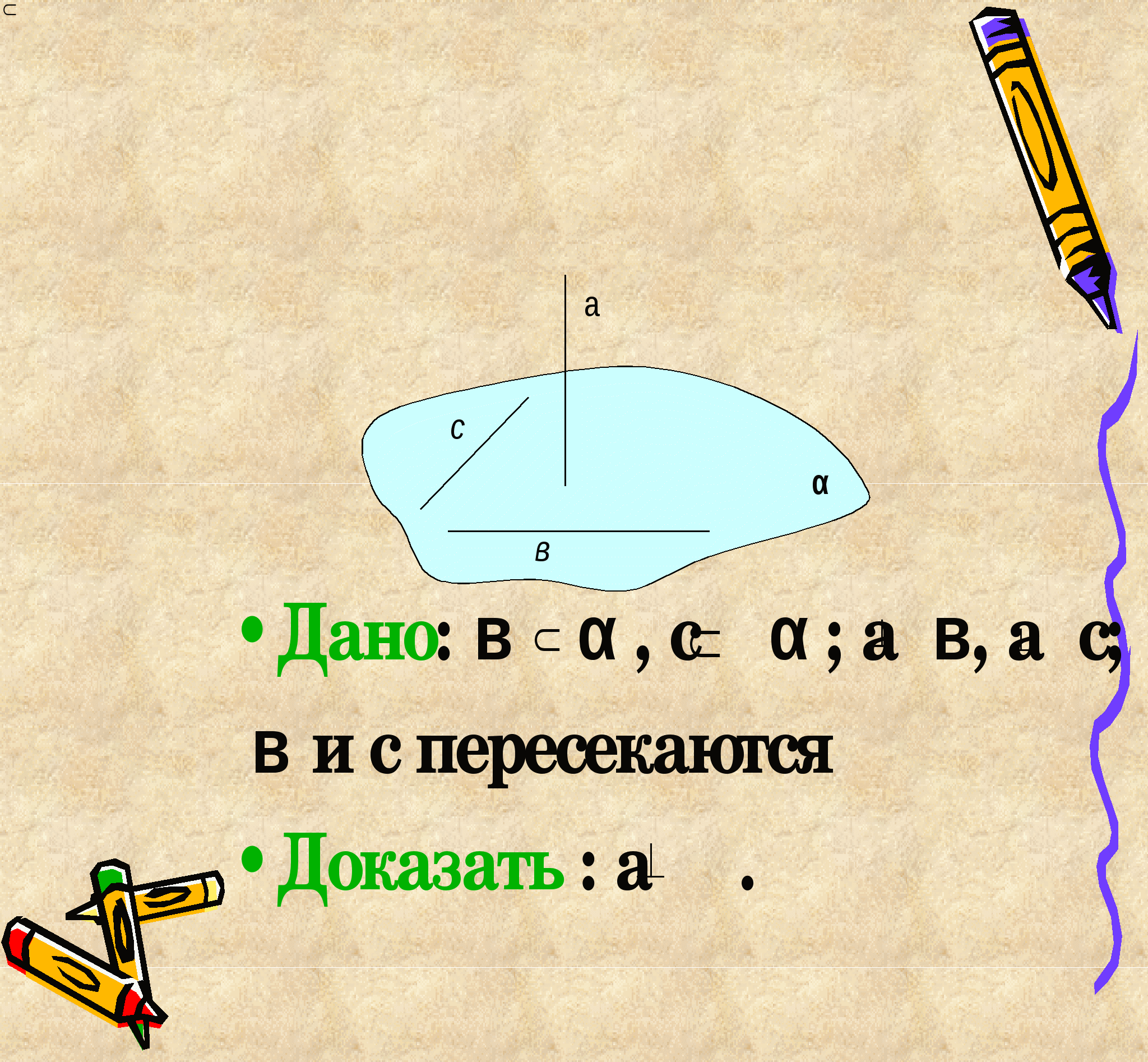       Заключение. Данная работа представляет практический интерес для учителей, работающих в профильных классах. Использованные в работе материалы уже были мною апробированы при работе в 10 классе естественно-математического профиля. В работе использованы конспекты уроков, проведенных мною на семинарах для учителей математики Мглинского района и при проведении предметных курсов по математике от БИПКРО. Практические разработки являются образцами, по которым можно разрабатывать уроки для изучения других тем курса стереометрии, поэтому будут полезны другим учителям. Список литературы.
|