Ларькова тамара павловна
 Скачать 373.02 Kb.
|
10- 11 класс- Умение самостоятельно и мотивированно организовывать свою познавательную деятельность ( от постановки цели до получения и оценки результата). Использование элементов причинно-следственного и структурно-функционального анализа. - Исследование несложных реальных связей и зависимостей. Определение сущностных характеристик изучаемого объекта; самостоятельный выбор критериев для сравнения, сопоставления, оценки и классификации объектов. - Участие в проектной деятельности, в организации и проведении учебно-исследовательской работы: выдвижение гипотез, осуществление их проверки, владение приемами исследовательской деятельности, элементарными умениями прогноза (умение отвечать на вопрос « Что произойдет, если …»). Самостоятельное создание алгоритмов познавательной деятельности для решения задач творческого и поискового характера. Формулирование полученных результатов. - Создание собственных произведений, идеальных и реальных моделей объектов, процессов, явлений, в том числе с использованием мультимедийных технологий, реализация оригинального замысла, использование разнообразных (в том числе художественных) средств, умение импровизировать. Учебно – интеллектуальные умения и навыки Деятельность учителя: - систематически работает над интеллектуальными умениями - реализует межпредметную методику их формирования - согласовывает свои обучающие и контролирующие действия с другими учителями - опирается на уже известные детям умения - вводит умение в практическую деятельность учащихся - вводит умение с объяснением теоретической основы приема - работает над дальнейшим развитием умения Деятельность ученика: - применяет умение правильно, уверенно - допускает ошибки, используя операции не полностью - не владеет интеллектуальным умением (каким?) В стандартах среднего (полного) общего образования изучение математики на базовом уровне направлено на достижение следующих целей:
Организация исследовательской работы учащихся на уроках геометрии Существенную роль в усилении прикладной и практической направленности курса геометрии и одновременно в развитии способностей учащихся к самостоятельным исследованиям играют задания, выполнение которых представляет собой относительно завершенный исследовательский цикл: наблюдение – гипотеза – проверка гипотезы. В качестве таких заданий целесообразно использовать исследовательские работы. Исследовательские работы удачно вписываются в общую структуру учебного процесса, позволяя связать отдельные вопросы курса геометрии между собой и с курсами алгебры и физики, усиливает прикладную и практическую направленность курса математики, является эффективным средством повышения активности школьников. Часть исследовательских работ может быть реализована не только на уроке, но и в качестве домашнего задания. В последнем случае на уроке обсуждаются результаты, полученные учащимися дома. Исследовательская работа по теме « Площадь прямоугольника», 7класс.
При каком значении X у вас получился прямоугольник наибольшей площади? Каково наибольшее из полученных значений S ? Выберите сами два каких–либо допустимых значения X и вычислите соответствующие им значения S . Удалось ли вам получить S , больше, чем найденное ранее? Какую гипотезу можно высказать на основании проведенного исследования о форме прямоугольника наибольшей площади, имеющего данный периметр?
. В А . . С Учитывая, что можно построить сколько угодно вписанных таким образом прямоугольников, постройте самостоятельно прямоугольники с высотами, указанными в таблице, измерьте основание каждого прямоугольника и вычислите его площадь. Результаты запишите в таблицу.
При каком значении h у вас получился прямоугольник наибольшей площади? Какова его площадь? Сравните высоту, основание и площадь этого прямоугольника соответственно с высотой, основанием и площадью треугольника АВС. Какую гипотезу можно высказать в результате этого исследования? Эти работы осуществляют пропедевтику геометрических задач на экстремум. Необходимые для строгого обоснования гипотезы знания учащиеся получат в курсе VIII класса. Творческие задания как средство активизации познавательной деятельности учащихся. Самостоятельное приобретение учащимися новых знаний- творческий процесс. Большую помощь при этом оказывает введение в обучение творческих заданий, одним из видов которых являются задания по составлению задач. Такие задания могут быть предложены учащимся как на этапе изучения нового материала, так и на этапе его закрепления. Рассмотрим задания по составлению геометрических задач на доказательство, при выполнении которых учащиеся получают более глубокие знания о структуре задачи и процессе ее решения, что в свою очередь способствует развитию их интереса к поиску нового. В общем случае механизм составления задач на доказательство может быть описан с помощью следующей последовательности действий: 1). Выбор объектов и целей их исследования; 2). Анализ полученной заданной ситуации; 3). Получение нового знания об объектах задачи; 4). Формулировка задачи на доказательство полученного факта; 5). Решение составленной задачи. Анализ задачной ситуации может осуществляться двумя способами: а). на основе построений и измерений; б). с помощью вывода логических следствий из выбранных условий. В первом случае сначала выдвигается гипотеза, которая становится новым знанием только после её доказательства, т.е. после решения составленной задачи. Во втором же случае полученное новое знание не нуждается в дополнительном доказательстве, поэтому решение составленной задачи служит контролем правильности её постановки. Механизм составления задач определяет методику организации деятельности учащихся по выполнению заданий, которые должны содержать некоторую задачную ситуацию и цель её исследования (в отдельных случаях цель исследования может быть определена самими учащимися под руководством учителя). Организация дальнейшей работы по составлению задач зависит от метода поиска нового знания. Рассмотрим деятельность учащихся по составлению задач с помощью вывода из данных условий логических следствий (дедуктивный метод получения новых знаний). Этот метод тесно связан с поиском способа решения готовой задачи на доказательство, разница лишь в том, что в готовой задаче уже известен результат, справедливость которого нужно доказать, процесс же составления задачи направлен на его получение. Задания на составление задач по теме « Четырехугольник», 8 класс.
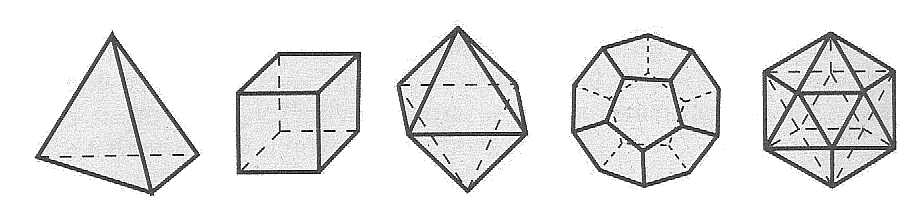
1). Докажите, что середины сторон четырехугольника являются вершинами параллелограмма. 2). Докажите, что отрезки, соединяющие середины противоположных сторон четырехугольника, делятся точкой их пересечения пополам. 2. Найдите, при каком условии четырехугольник, вершинами которого служат середины сторон данного четырехугольника, является прямоугольником. Составьте задачи на доказательство. 1). В четырехугольнике диагонали взаимно перпендикулярны. Докажите, что середины сторон этого четырехугольника, являются вершинами прямоугольника. 3. Середины диагоналей трапеции соединены отрезком. Составьте задачу по данной задачной ситуации. 1). Докажите, что отрезок, соединяющий середины диагоналей трапеции, параллелен основаниям и равен полуразности оснований. Приведенные здесь задания выполняются с помощью выделения логических следствий. Познавательные задачи- проблемы учат учащихся наблюдать и анализировать, высказывать гипотезы. Они дают возможность повторять изученный материал и подводят к доказательству новых теорем. Использованием проектно- исследовательской технологии, 11 класс. Учащиеся 11 класса при изучении темы « Многогранники» должны иметь представление о правильных многогранниках (тетраэдр, куб, октаэдр, додекаэдр, икосаэдр). Тема урока: « МНОГОГРАННИКИ » (с использованием проектно- исследовательской технологии). Цель урока:
Вид урока: урок – исследование. Тип урока: усвоение новых знаний. Используемые методы обучения: проблемное изложение материала, исследовательская работа. Формы обучения: конференция, исследовательская лабораторная работа. Оборудование:
3. Таблицы, изображение «Космический кубок» Кеплера (модели Солнечной системы) 4. Репродукция картины«Тайная вечеря» Сальвадора Дали . Были созданы и в течение некоторого времени работали группы учеников: 1 группа – историки, 2 группа – математики, 3 группа – исследователи космической теории платоновых тел, теории Кеплера, 4 группа – биологи и географы, 5 группа – архитекторы, 6 группа – искусствоведы. Каждый из них выбрал направление исследования по своему желанию, и поэтому была проведена большая работа каждой из групп. . 1. Группа «математиков» дает понятие правильного многогранника и определяет, сколько их существует в природе. 1)Многогранник - геометрическое тело, ограниченное со всех сторон плоскими многоугольниками, называемыми гранями. Стороны граней называются ребрами многогранника, а концы ребер — вершинами многогранника. По числу граней различают четырехгранники, пятигранники и т. д. Многогранник называется выпуклым, если он весь расположен по одну сторону от плоскости каждой из его граней. Выпуклый многогранник называется правильным, если все его грани — правильные одинаковые многоугольники и все многогранные углы при вершинах равны. Очевидно, что ребра правильного многогранника равны между собой. Можно сказать, что равны также все двугранные углы, содержащие две грани с общим ребром. В природе известны пять правильных многогранников: тетраэдр, куб, октаэдр, додекаэдр, икосаэдр. Форма первоэлемента Земли - куб, Воздуха - октаэдр, Огня - тетраэдр, Воды - икосаэдр, а всему миру творец придал форму пятиугольного додекаэдра. О том, что Земля имеет форму шара, учили Пифагорейцы. По Пифагору, существует 5 телесных фигур: высшее божество само построило Вселенную на основании геометрической формы додекаэдра. Земля подобна Вселенной, и у Платона Земля – тоже додекаэдр. (Сальвадор Дали. Тайная вечеря (1955))
Изучая любые многогранники, естественнее всего подсчитать, сколько у него граней, сколько ребер и вершин. Подсчитаем и мы число указанных элементов правильных многогранников и зафиксируем результаты в таблице 1. Таблица 1
Рассматривая табл. 1, зададимся вопросом: «нет ли закономерности в возрастании чисел в каждом столбце?» По-видимому, нет. Вот в столбце «грани» все сначала пошло хорошо (4 + 2 = 6, 6 + 2 = 8), а потом намеченная закономерность «провалилась» (8 + 2   ). В столбце «вершины» нет даже стабильного возрастания. Число вершин то возрастает (от 4 до 8, от 6 до 20), а то и убывает (от 8 до 6, от 20 до 12). В столбце «ребра» закономерности тоже не видно.Но не будем сдаваться. У нас еще есть поле для эксперимента. Ведь мы сравнивали числа внутри одного столбца. Но можно рассмотреть сумму чисел в двух столбцах, хотя бы в столбцах «грани» и «вершины» (Г + В). Сравним новую таблицу своих подсчетов (см. табл. 2 Таблица 2.
Вот теперь закономерность видна. Сформулируем ее так: «Сумма числа граней и вершин равна числу ребер, увеличенному на 2»: Г + В = Р + 2. Итак, получена формула, которая была подмечена уже Декартом в 1640 г., а позднее переоткрыта Эйлером (1752), имя которого с тех пор она и носит. Формула Эйлера верна для любых выпуклых многогранников. 2). Зададимся теперь вопросом о том, сколько правильных многогранников существует. Доказательство того, что существует ровно пять правильных выпуклых многогранников, очень простое. Рассмотрим развертку вершины такого многогранника. Каждая вершина может принадлежать трем и более граням. Сначала рассмотрим случай, когда грани многогранника - равносторонние треугольники. Поскольку внутренний угол равностороннего треугольника равен 60°, три таких угла дадут в развертке 180°. Если теперь склеить развертку в многогранный угол, получится тетраэдр - многогранник, в каждой вершине которого встречаются три правильные треугольные грани. Если добавить к развертке вершины еще один треугольник, в сумме получится 240°. Это развертка вершины октаэдра. Добавление пятого треугольника даст угол 300° - мы получаем развертку вершины икосаэдра. Если же добавить еще один, шестой треугольник, сумма углов станет равной 360° - эта развертка, очевидно, не может соответствовать ни одному выпуклому многограннику. Теперь перейдем к квадратным граням. Развертка из трех квадратных граней имеет угол 3x90°=270° - получается вершина куба, который также гексаэдром. Добавление еще одного квадрата увеличит угол до 360° - этой развертке уже не соответствует никакой выпуклый многогранник. Три пятиугольные грани дают угол развертки 3*108°=324° - вершина додекаэдра. Если добавить еще один пятиугольник, получим больше 360°. Для шестиугольников уже три грани дают угол развертки 3*120°=360°, поэтому правильного выпуклого многогранника с шестиугольными гранями не существует. Если же грань имеет еще больше углов, то развертка будет иметь еще больший угол. Значит, правильных выпуклых многогранников с гранями, имеющими шесть и более углов, не существует. Таким образом, мы убедились, что существует лишь пять выпуклых правильных многогранников - тетраэдр, октаэдр и икосаэдр с треугольными гранями, куб (гексаэдр) с квадратными гранями и додекаэдр с пятиугольными гранями. 2.Группы «архитекторов» знакомит учащихся с моделями правильных многогранников. Платоновы тела - это трехмерный аналог плоских правильных многоугольников. Однако между двумерным и трехмерным случаями есть важное отличие: существует бесконечно много различных правильных многоугольников, но лишь пять различных правильных многогранников. Доказательство этого факта известно уже более двух тысяч лет; этим доказательством и изучением пяти правильных тел завершаются "Начала" Евклида. Группа «архитекторов» подготовила модели каждой из платоновых тел. Для подготовки технологических карт изготовления моделей наша группа воспользовалась рекомендациями, данными в книге М. Винниджера «Модели многогранников», М., 1975. «Автор этой книги, заражая своим энтузиазмом читателя, дает ему ясные и четкие указания о том, как изготовить модели различных многогранников. Объяснения проиллюстрированы фотографиями моделей из собрания автора – возможно, наиболее полного в настоящее время. Но фотографии не в состоянии передать всего великолепия самих моделей. Наиболее сложные «курносые» модели не только крайне трудны в изготовлении, но и весьма декоративны. Это ли не превосходный пример родства истины и красоты!» – отмечает в предисловии к книге Г.С.М. Кокстер. М. Винниджер отмечает: «Время, которое я затратил на изготовление моделей невыпуклых однородных многогранников, в существенной степени зависело от характера модели. Так, на простейшие из них требовалось более трех-четырех часов, а в среднем же приходилось затрачивать восемьдесят часов, а некоторые сложные модели занимали двадцать-тридцать часов. Две модели отняли у меня свыше сотни часов каждая. Теперь, когда работа завершена, я, пожалуй, соглашусь с тем, что ее объем поразил и меня. Но китайская пословица гласит «Если ты собираешься пройти тысячу ли, начни с того, что сделай первый шаг». За первым шагом последует другой, и вскоре красота открывшихся взору путника видов заставит его забыть о трудностях пути». 1 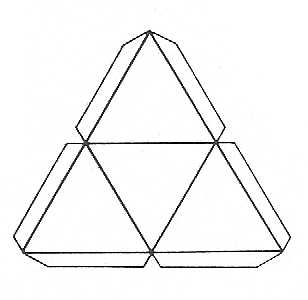 )П 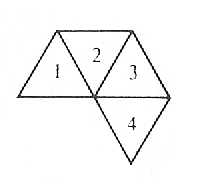 ростейшим среди правильных многогранников является тетраэдр. Его четыре грани – равносторонние треугольники. Четыре – это наименьшее число граней, отделяющих часть трехмерного пространства. Тем не менее тетраэдр обладает многими свойствами, характерными для однородных многогранников. Все его грани суть правильные многоугольники, причем каждая отделяется ребром в точности от одной грани. Все многогранные углы тетраэдра равны между собой. Модель тетраэдра можно сделать, пользуясь одной разверткой, на которой будут расположены все четыре треугольные грани. Чтобы изготовить модель, достаточно склеить боковые грани. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
