|
Решение задачи
Справочный материал
|
Виды комбинаций
|
Без повторений
|
С повторениями
|
Перестановки
|
перестановками из n различных элементов называются размещения из этих n элементов по n
|
Pn=n!
|
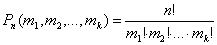
|
Размещения
|
размещениями из n различных элементов по k элементов называются комбинации, составленные из данных
n элементов по k элементов
|
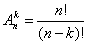
|
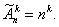
|
Сочетания
|
сочетаниями из n элементов по k элементов называется любое подмножество, которое содержит k различных
элементов данного множества
|
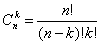
|
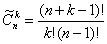
|
Задачи.
Размещения с повторениями
Условие задачи
|
Решение задачи
|
1. Каждый телефонный номер состоит из 7 цифр. Сколько существует телефонных номеров, не содержащих других цифр, кроме
2, 3, 5 и 7?
|
Основное множество: {2, 3, 5, 7}
соединение – семизначный телефонный номер
2233447 7443322 порядок важен задана последовательность это либо размещения, либо перестановки. Так как семизначный номер может включать не все элементы основного множества (например, номер 2223332 не содержит цифр 5, 7), а лишь некоторые из них, то это размещения в семи разных местах семи цифр, выбранных из четырех разных цифр с повторениями каждой из них любое число раз, но не более семи.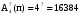 Ответ: 16384 Ответ: 16384
|
2. Сколькими способами можно разместить 8 пассажиров в три вагона?
|
Эту задачу можно рассматривать как задачу о числе распределения среди восьми пассажиров любых восьми выбранных из трех вагонов с повторениями каждого из них любое число раз, но не более восьми.
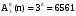 Ответ: 6561 Ответ: 6561
|
3. Буквы азбуки Морзе состоят из символов – точка и тире. Сколько букв получим, если потребуем, чтобы каждая буква состояла не более чем из пяти указанных символов?
|
Число всех букв, каждая из которых записывается одним символом, равно 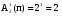 . .
Число всех букв, каждая из которых записывается двумя символами, равно 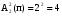 . .
Число всех букв, каждая из которых записывается тремя символами, равно 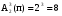 . .
Число всех букв, каждая из которых записывается четырьмя символами, равно 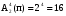 . .
Число всех букв, каждая из которых записывается пятью символами, равно 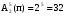 . .
Число букв согласно требованию задачи (по правилу сложения) равно 2+4+8+16+32=62. Ответ: 62
|
4. Сколько различных 10-буквенных слов можно составить, используя только две буквы: а и b?
|
Решение: это задача о числе возможностей разместить на 10 различных местах любые 10 букв, выбранных из букв а и b, с повторениями каждой из них любое число раз, но не более 10.
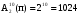 Ответ: 1024 Ответ: 1024
|
Перестановки с повторениями.
5. Сколькими способами можно расположить в ряд две зеленые и четыре красные лампочки?
|
Порядок важен и в соединении участвуют все элементы без исключения: зеленые лампочки – 2 раза, а красные – 4 раза.
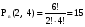 способов. Ответ: 15 способов. Ответ: 15
|
6. Сколько всех семизначных чисел, у каждого из которых цифра 6 встречается три раза, а цифра 5 – четыре раза?
|
Порядок важен и в соединении участвуют все элементы без исключения: шестерки – 3 раза, а пятерки – 4 раза.
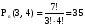 чисел. Ответ: 35 чисел. Ответ: 35
|
7. Сколькими способами можно переставить буквы в слове «математика», чтобы получались всевозможные различные анаграммы?
|
Порядок важен и в соединении участвуют все элементы без исключения: буква «м» – 2 раза, буква «а» – 3 раза, буква «2», буквы «е», «и», «к» - по 1 разу. 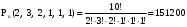 способами способами
Ответ: 151200
|
8. Сколькими способами можно 10 человек разбить на три группы соответственно по 2, 3, 5 человек в группе?
|
Порядок важен и в соединении участвуют все элементы без исключения: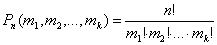
Р10 (2,3,5)=10!/2!.3!.5!=2520
Ответ:2520
|
Сочетания с повторениями.
9. Сколькими способами можно выбрать 4 монеты из четырех пятикопеечных монет и из четырех двухкопеечных монет?
|
Порядок выбора монет неважен, и примерами соединений могут являться {5,5,5,5}, {2,2,2,2}, {5,2,5,5} и т.д. Это задача о числе сочетаний 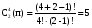
Ответ: 5
|
10. В кондитерской имеется 5 разных сортов пирожных. Сколькими способами можно выбрать набор из 4 пирожных?
|
Это задача о числе сочетаний из 5 видов пирожных по 4 с повторениями.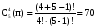 способов способов
Ответ: 70
|
11. Сколько всего чисел можно составить из цифр 1, 2, 3, 4, 5, в каждом из которых цифры расположены в неубывающем порядке?
|
Это задача о числе сочетаний из 5 цифр по одному, по два, по три, по четыре и по пяти с повторениями в каждом случае
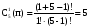 ; ; 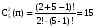 ; ; 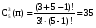 ; ;
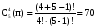 ; ; 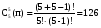
Согласно правилу сложения: 5+15+35+70+126=251 чисел
Ответ: 251
|
10. Сколько будет костей домино, если в их образовании использовать все цифры?
|
Число костей домино можно рассматривать как число сочетаний из 10 чисел по 2 с повторениями.
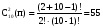 костей костей
Ответ: 55
| |
|
|
 Скачать 45 Kb.
Скачать 45 Kb.