Конспект урока по информатике в подгруппе учащихся 11-ого класса Тема урока: «Финансовая математика в нашей жизни»
 Скачать 64.81 Kb. Скачать 64.81 Kb.
|
| Конспект урока по информатике в подгруппе учащихся 11-ого класса Тема урока: «Финансовая математика в нашей жизни». Цель урока: показать применение ИКТ на интегрированном уроке информатики, математики и экономики в процессе моделирования жизненных ситуаций взаимодействия «Банк - клиент». Задачи урока: Познавательные - познакомить учащихся с ситуациями, при которых возникает необходимость разбираться в финансовых операциях. Обучающие - научиться разрешать возникшие финансовые и экономические проблемы с помощью математического аппарата и компьютерных технологий. Приобрести новые знания по математике и по информатике в области финансовой деятельности. Развивающие - развить кругозор в области применения процессора Excel, встроенных функций и практического приложения теории по «Основам экономики». Воспитательные - выработать целостный подход к изучаемым дисциплинам, интерес ко всем наукам, их взаимосвязи, поднять мотивации учащихся и умения работы в группе. Оборудование: компьютеры, макбуки, проектор и экран. Ход урока:
Вводное слово. В повседневной жизни финансовая математика наша сводится к 4 арифметическим действиям. Но ситуация усложняется, когда речь идет о небольших коммерческих операциях, не говоря уже о банковской деятельности - это и сумма кредитов, срок и способ погашения, себестоимость, цена товара и прибыль, налоги и заполнение деклараций. Занятие бизнесом требует глубокого анализа последствий принятых решений. Необходимы определенные знания в области финансовой математики, так как в коммерческих и финансовых расчетах применяются методы математического анализа, теории вероятностей, математической статистики, теории игр, теории оптимизации – это солидные разделы экономики, математики и информатики. Тема урока выбрана не случайно. Во взрослой жизни придется иметь дело с банковской системой, с коммерцией и бизнесом. В процессе урока должно сложиться новое представление о математике как науке, удовлетворяющей практические потребности бизнеса. На уроке в результате выполнения финансовых расчетов, которые встретятся вам в жизни, мы увидим, как в этих ситуациях применить табличный процессор Excel и, используя его возможности, строить новые модели, варьируя аргументами встроенных финансовых функций. Для реализации первого проекта мы не использовали готовые разработки, а сами на предыдущем занятии по информатике написали программу, которая рассчитывает сумму вклада на депозите при определенных условиях. Задание 1. Создать проект в VB пользовательской формы и написать командный код для расчета суммы вклада на депозите при определенных условиях - с клавиатуры вводится первоначальная сумма S, банковский процент Р и срок депозита Т. Учащиеся на рабочих местах загружают созданную дома пользовательскую форму, при этом процесс выполнения задания учеником, сидящим за первым компьютером, проектируется на экран. На экране появляется форма и программный код к нему. 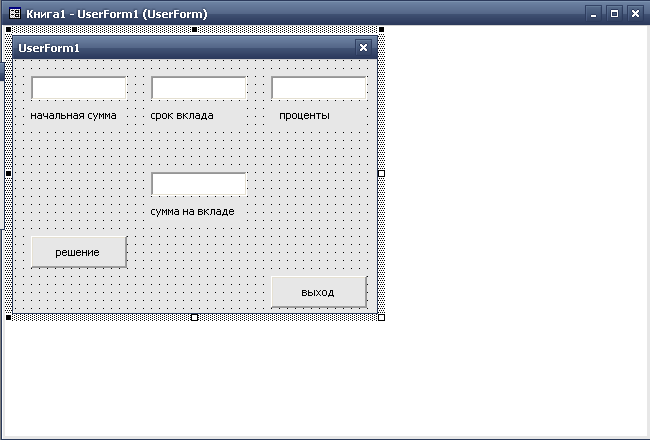  Учитель проверяет работу каждого ученика в сети и непосредственно. Подставляя конкретные данные при запросе программы, учащиеся получают результат аккумуляции средств на вкладе по формуле сложных процентов. Результат работы программы появляется на экране. 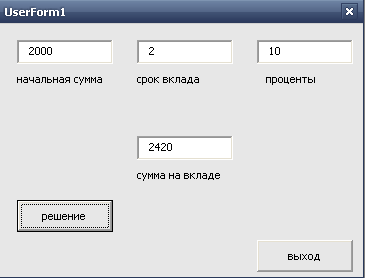 Учащиеся проигрывают другие ситуации. Учитель видоизменяет данное задание и на экране – две новые задачи. Задача 2. Рассчитать первоначальный взнос, если через два года в вашем распоряжении должна быть необходимая сумма в 25000 руб. для покупки компьютера при тех же банковских 10% начислениях. На экране появляется уравнение, проектируемое учащимся с первой парты 25000=Х*(1+0,1)^2. Задача 3. Рассчитать период, за который начальная сумма 5000 достигнет желаемой суммы 30000 при тех же 10% начислениях. На экран проектируется уравнение 30000=5000*(1+0,1)^x Задачи №2 и №3 решаются математически с использованием формулы сложных процентов, которая изучалась на уроке экономики в теме «Как банки делают деньги». К проектору выходит тот ученик, который раньше и верно решил уравнение. Решение проверяется учителем через сеть. На экране
Дальнейшее моделирование условия задачи1, т.е. выбор новых данных или изменение одновременно двух и трех условий в первоначальной задаче 1, требует от учащихся сложных математических вычислений или написания программ и их отладки, что связано с ресурсом времени и не входит в цели урока. Поэтому на помощь вызываем электронный процессор Excel. Решаем задачу с помощью встроенных финансовых функций.
Норма – процентная ставка за период; Выплата – возможные постоянные выплаты за период; Нз – начальное значение суммы; Бс – баланс наличности; Тип – 1 или 0, означающие, когда производятся выплаты. Если аргумент равен 1, то в начале, 0 - в конце периода. 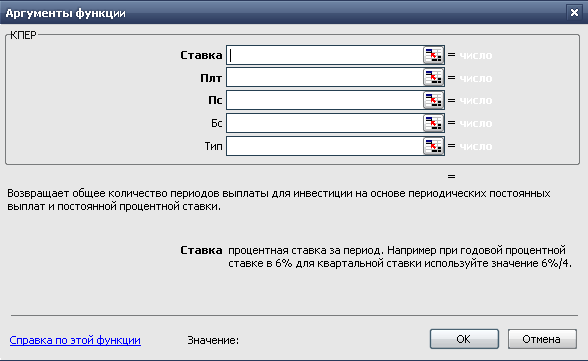 Учитель объясняет синтаксис функции, возможности каждого аргумента и область применения названной функции. В качестве примера на экран проектируется функция КПЕР(10%/12;-1000;-5000; 30000;1), что соответствует решению следующей задачи: Рассчитать, сколько месяцев понадобится для накопления суммы в 30000 руб., если первоначальная сумма вклада равна 5000 руб., процент по депозиту равен 10% годовых и есть возможность ежемесячно пополнять вклад постоянными платежами в 1000 руб.? Учитель обращает внимание учащихся на знак «-», поясняя, что в этой ситуации они выступают в качестве кредитора. В начале периода они лишаются суммы, а в конце возвращают с процентами. Учащиеся решают все три задачи при заданных данных, чтобы сверить ответы и убедиться в правильном выборе финансовой функции. Затем проигрывают различные ситуации, меняя данные и аргументы функции, особо экспериментируя с последним аргументом - тип, так как начало и конец периода существенно влияют на достижение цели. Задача 4. Взят кредит на определенный срок и под данный процент. Требуется определить величину платежа за нужный период в счет погашения ссуды. Решаем при помощи новой финансовой функции
Норма – процентная ставка по ссуде; Кпер – общее число выплат; Нз – основная сумма, которую составят будущие платежи; Бс – баланс наличности после последней выплаты; Тип – 1 или 0, означающие, когда производятся выплаты. Если аргумент равен 1, то в начале, 0 - в конце периода Учитель у доски (на экране) объясняет назначение данной функции, ее возможностях, особенно подробно останавливаясь о роли аргументов. На примере функции ОСПЛАТ (14%/12; 10;10000;0;0), ученики узнают, чему равны ежемесячные выплаты по займу в 10000 руб. и годовой процентной ставке 14% при сроке погашения кредита 10 месяцев. Здесь бс равно 0, так как за 10 месяцев мы полностью погашаем задолженность по кредиту. Проверяем возможности этой функции, введя изменение суммы кредита или срока займа, ссудного процента, типа выплаты и их комбинаций. Функция позволяет моделировать ситуации и при одновременном изменении нескольких аргументов. ОСПЛТ позволяет также вести расчеты для накопления суммы вклада за определенный период, то есть определить размер откладываемой суммы. Предположим, что родителям к окончанию школы необходимо накопить 100000 руб. Они открывают в первом классе депозитный счет на имя сына под 8% годовых. Формула расчета размера ежемесячной откладываемой суммы выглядит так: ОСПЛАТ(8%/12; 11*12; 0; 100000). Таким образом, задание 1 при различных условиях можно решать и с функцией ОСПЛТ. Домашнее задание. Задача1. Для покупки автомобиля недостающую сумму 250000 руб. берем в заем сроком на 2 года с процентной ставкой18% годовых. Найти размер ежемесячной выплаты денег банку. Задача2. Рассчитать, через сколько лет вклад размером 50000 руб. достигнет 500000 руб. при условии, что процентная ставка по вкладу равна 12% годовых, начисление процентов производится ежеквартально. Заключительное слово учителя: Эти два часа были уроками приобретения новых знаний, хотя со многими экономическими понятиями учащиеся знакомы по курсу «Основы экономики», в частности о деятельности банков знают по теоретическим положениям «Как банки делают деньги». Сегодня мы получили практическое подтверждение некоторым скрытым банковским приемам при изучении финансовых функций. Взаимосвязь трех изучаемых предметов открывает новые возможности в самостоятельном приобретении знаний. Существуют не менее важные функции, которые позволяют разрешать жизненные ситуации в условиях рыночной экономики. Полученные знания и сегодняшний практический опыт помогут вам грамотно вести бизнес, сотрудничать с банком, быть успешными в жизни. Прошу вас подвести итоги нашего урока. Выводы (выводы делают учащиеся).
Открытый урок «Финансовая математика в нашей жизни» был проведен на общегородском семинаре «Развитие познавательных интересов учащихся на уроках при использовании компьютерных технологий», который состоялся в МОУСОШ №8 в 11-ом инженерно - экономическом классе, на котором присутствовали 16 учителей математики, физики, информатики, методисты ГМО. Урок получил высокую оценку со стороны коллег. |