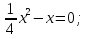Урока алгебры в 8 классе по теме «Определение квадратного уравнения. Неполные квадратные уравнения»
 Скачать 73.93 Kb. Скачать 73.93 Kb.
|
                Разработка прблемно-эвристического урока алгебры в 8 классе по теме «Определение квадратного уравнения. Неполные квадратные уравнения». Разработка прблемно-эвристического урока алгебры в 8 классе по теме «Определение квадратного уравнения. Неполные квадратные уравнения».А.Н. Беседина, учитель математики МБОУ «Тростенецкая средняя общеобразовательная школа Новооскольского района Белгородской области» Цели урока: 1) получить знания о квадратных уравнениях, исследовать различные виды неполных квадратных уравнений и определить способы их решения, получить навык решения неполных квадратных уравнений; 2) развивать познавательный интерес к математике, к поисково-исследовательской деятельности; 3) воспитание организованности и самостоятельности в работе. Оборудование: компьютер, проектор, презентация, карточки-задания. Тип урока: урок изучения нового учебного материала. Ход урока
Учитель. Представьте себе, что сегодня вы не просто ученики 8 класса, а сотрудники научного математического общества, на заседании которого необходимо провести исследование по теме «Квадратные уравнения. Неполные квадратные уравнения». Как руководитель научного общества, я предлагаю вам следующий план проведения заседания: 1) Сообщение о квадратных уравнениях. 2) Исследовательская групповая работа над проблемой решения неполных квадратных уравнений. 3) Выступления членов групп по данной проблеме. 4) Самостоятельная работа. 5) Подведение итогов работы научного общества. 2. Актуализация опорных знаний и умений учащихся.(5 мин.) Устные упражнения: 1). Является ли число а корнем уравнения: а) 2х – 7 = 8, а = 7,5; б) х2 – х – 20 = 0, а = 5; в) (х3 + 12) (х2 – 8) = 0, а = 2). Найдите корни уравнения: а) (х – 3 ) (х + 12) = 0; б) (6х – 5) (х + 5) = 0; в) (х – 8) (х + 2) (х2 + 25) = 0. г) х2 = 0; д) х2 = 16; е) х2 = 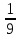 ; ж) х2 = 144; ; ж) х2 = 144;з) х2 = 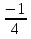 ; и) х2 = ; и) х2 = 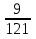 ; к) х2 = 2,56; л) х2 = ; к) х2 = 2,56; л) х2 = 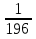 . .3. Получение и первичное закрепление новых знаний.(30 мин.) 1) Сообщение о квадратных уравнениях. На доске записаны уравнения: 3х² - 6 = 0; 2х² - 8х + 7 = 0; -9х² = 0; -7х² + 4х = 0; х² - 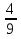 = 0; -2х² + 0,8 = 0. Чем схожи данные уравнения? = 0; -2х² + 0,8 = 0. Чем схожи данные уравнения?Определение квадратного уравнения. ( слайд2) Устные упражнения: 1) Назвать коэффициенты квадратных уравнений, записанных на доске; 2) Выполнить устно № 504, № 505. 2) Постановка проблемы: Как решать такие уравнения?(Слайд3) Историческая справка. Необходимость решать уравнения не только первой, но и второй степени еще в древности была вызвана потребностью решать задачи, связанные с нахождением площадей земельных участков и с земляными работами военного характера, а также с развитием астрономии и самой математики. Квадратные уравнения умели решать около 2000 лет до н.э. вавилоняне. Несмотря на высокий уровень развития алгебры в Вавилоне, в их клинописных текстах отсутствуют понятие отрицательного числа и общие методы решения квадратных уравнений. (слайды4-7) В Древней Индии в астрономических трактатах содержится общее правило решения квадратных уравнений. В Индии были распространены публичные соревнования в решении трудных задач. В одной из старинных индийских книг говорится по поводу таких соревнований следующее: «Как солнце блеском своим затмевает звезды, так ученый человек затмит славу другого в народных собраниях, предлагая и решая алгебраические задачи». Задачи часто облекались в стихотворную форму. Вот одна из задач знаменитого индийского математика VII века Бхаскары: - Обезьянок резвых стая Всласть поевши, развлекалась. Их в квадрате часть восьмая На поляне забавлялась. А двенадцать по лианам Стали прыгать, повисая… Сколько ж было обезьянок, Ты скажи мне, в этой стае? В Европе способы решения квадратных уравнений были впервые изложены в «Книге абака», написанной в 1202 году итальянским математиком Леонардо Фибоначчи. Эта книга способствовала распространению алгебраических знаний не только в Италии, но и в Германии, Франции и других странах Европы. Многие задачи из «Книги абака» переходили почти во все европейские учебники XVI-XVII в.в. и частично XVIII в. И лишь в XVII в. Благодаря трудам Жирара, Декарта, Ньютона и других ученых способ решения квадратных уравнений принимает современный вид. Русский же читатель впервые познакомился со способами решения квадратных уравнений по книге Л.Ф. Магницкого «Арифметика». Сегодня на нашем заседании мы рассмотрим и исследуем способы решения неполных квадратных уравнений. -Какие уравнения называются неполными квадратными? Приведите примеры таких уравнений. -Разбейте уравнения на полные и неполные: а) 9х² = 0; б) 3х + х² + 1 = 0; в) 2х² - 32 = 0; г) х² + 4х = 0; д) 2х² + 5х – 7 = 0; е) 12 - х² + 3х = 0.(слайды8-10) Итак, ах² + вх + с = 0, где а 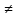 0, в = 0 или с = 0 или в = 0 и с = 0. 0, в = 0 или с = 0 или в = 0 и с = 0.а) ах² + с = 0, с 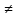 0. б) ах² + вх = 0, в 0. б) ах² + вх = 0, в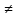 0. в) ах² = 0. 0. в) ах² = 0.Исходя из этого, перед вами стоит задача: исследовать неполные уравнения различных видов и предложить общий способ их решения. 3) Поисково-исследовательская деятельность учащихся. Учащиеся разделены на три группы. Каждой группе даны задания, включающие теоретическую и практическую части.
4) Выступления учащихся – сотрудников–«теоретиков» и сотрудников–«практиков» всех групп. «Теоретики» предлагают способы решения неполных квадратных уравнений разного вида. «Практики» у доски показывают решение двух уравнений каждого вида из указанного номера задания в учебнике. Остальные уравнения учащиеся решают самостоятельно, проверяют решение представители каждой группы. Алгоритм решения неполных квадратных уравнений учащиеся записывают в тетрадь.(слайд11)
a 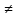 0, b=0, c=0 0, b=0, c=0ax2=0 a 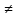 0, b 0, b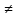 0, 0,c=0 a 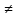 0, c 0, c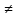 0, 0,b=0 x2=0 x=0 ax2+bx=0 ax2+c=0 ax2= 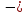 c cx2= 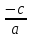 x(ax+b)=0 Имеет всегда 1 корень: Х = 0 x=0 или ax+b=0, ax= 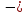 b, b,x= 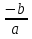 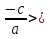 0 0x= 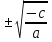 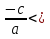 0 0Корней нет Имеет 2 корня: x= 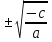
5) Применение квадратных уравнений при решении задач. Решаем № 516. х см – сторона квадрата. х² - 59 = 85, х² = 85 + 59 ; х² = 144; х = 12, х = -12 –не подходит по условию задачи. Ответ: 12 см. Самостоятельно решить № 517. Проверка с места комментированием.
-Уважаемые сотрудники, успешно ли проведено наше заседание? -Что узнали нового? Чего достигли? Каковы результаты нашей работы? -Что понравилось (не понравилось)? Благодарю за сотрудничество!
(2 мин.) |
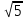 , х = -
, х = - 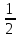 х² = 15 ; 3х² - 10х² = 0 ;
х² = 15 ; 3х² - 10х² = 0 ;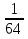 ; х² -64 = 0;
; х² -64 = 0; 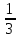 х²-х =0;
х²-х =0; 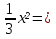 0; х²-0,01х = 0; х² =41;
0; х²-0,01х = 0; х² =41; 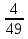 =0;
=0;