|
Урок алгебры в 9 классе по теме «Целые уравнения и его корни»
Методическая разработка урока. Дружкова Людмила Николаевна.
Урок алгебры в 9 классе
по теме «Целые уравнения и его корни»
РАЗРАБОТКА УРОКА
|
УУД
|
Орг. Момент
(Вводно-мотивационная часть, с целью активизации деятельности учащихся)
Учитель: Ребята что вы видите на экране?.(Уравнения)..А что с уравнениями обычно делают? (решают). А что значит решить уравнение?... И последний вопрос: Что называется корнем уравнения? …. Молодцы! Ребята, посмотрите, пожалуйста на экран! Данные уравнения отличаются друг от друга?
|
умение осознанно и произвольно строить речевое высказывание в устной форме;
анализ
построение логической цепи рассуждений, доказательство;
|
Учитель:. А теперь, прочитаете задание на слайде
Ребята давайте устно решим данные уравнения. Внимание на экран.
А) x2=0
|
Ж) x3-25x=0
|
Б) 3x-5=0
|
З) x(x-1)(x+2)=0
|
В) x2-5=0
|
И) x4+x2=-2
|
Г) x2=1/36
|
К) x2-0,01=0,03
|
Д) x2=-25
|
Л) 19-c2=10
|
Е) 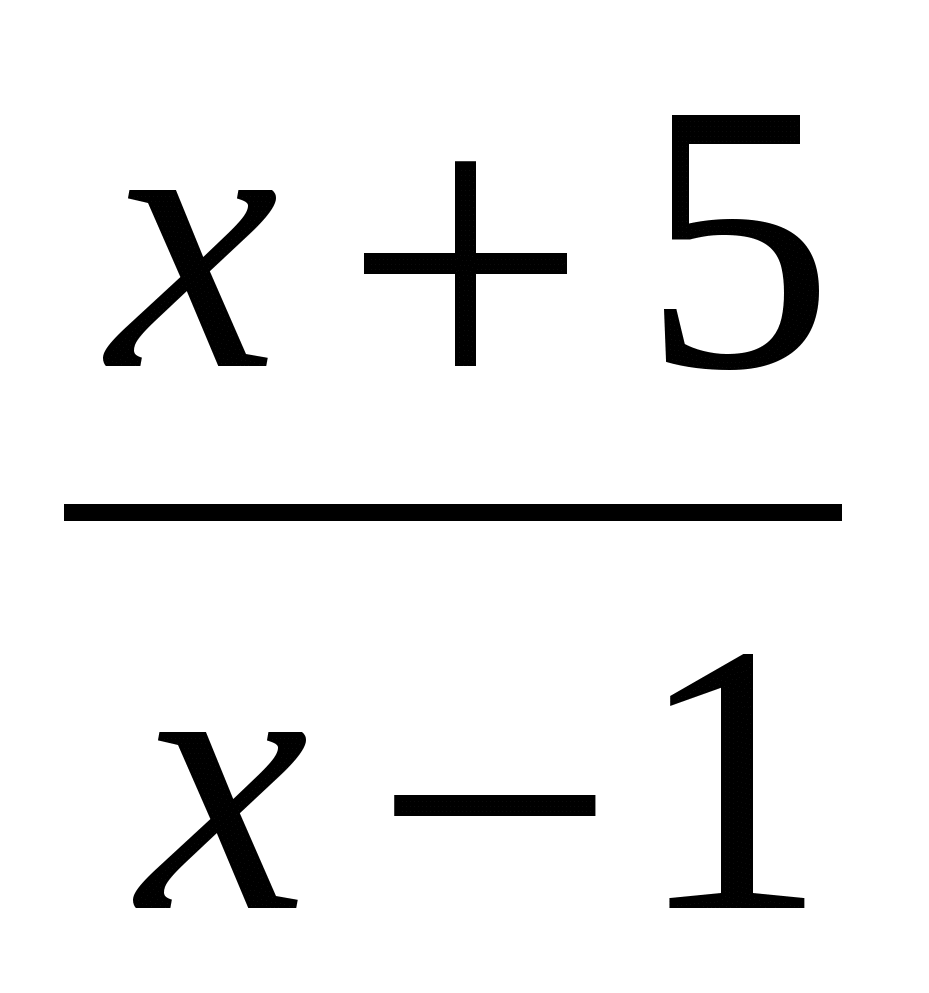 = 0 = 0
|
М) (x-3)2=25
|
Учитель: А теперь, ребята, попробуем указать из рациональных уравнений те которые не являются целыми.
Ученики: Называют целые и дробно-рациональные уравнения.
Учитель: Давайте сформулируем определение целого уравнения…
Ученики: Если левая и правая части представляют собой целые выражения, то это уравнение называется целым.
Учитель: Ребята, как вы думаете, чем мы будем заниматься на этом уроке?...... Попробуйте сформулировать цели нашего урока….
Учитель: Я с вами согласна. Тема нашего урока: “Целое уравнение и его корни” Сегодня мы познакомимся с целыми уравнениями, узнаем, как определить степень уравнения, рассмотрим способы решения целых уравнений. Откройте тетради. Запишите дату и тему урока
|
Анализ
сравнение
выбор оснований и критериев для сравнения,
классификации объектов
подведение под понятия,
умение осознанно и произвольно строить речевое высказывание в устной форме
Целеполагание
|
III. Изучение нового материала
Учитель: Ребята в начале урока мы с вами решали устно уравнения. Давайте вновь вернёмся к ним и укажем степени этих уравнений. А степенью целого уравнения называется степень равносильного ему уравнения вида Р(х) = 0, где Р(х) – многочлен стандартного вида. А что называется степенью многочлена?
Ученики: Наибольший показатель степени переменной входящей в уравнение называется степенью уравнения.
Учитель: Ребята, а какова степень знакомых нам уравнений? ………..
Учитель: С целыми уравнениями познакомились, а теперь порешаем. № 205
а)(6 – х)(х+6) – (х–11)х=36, б)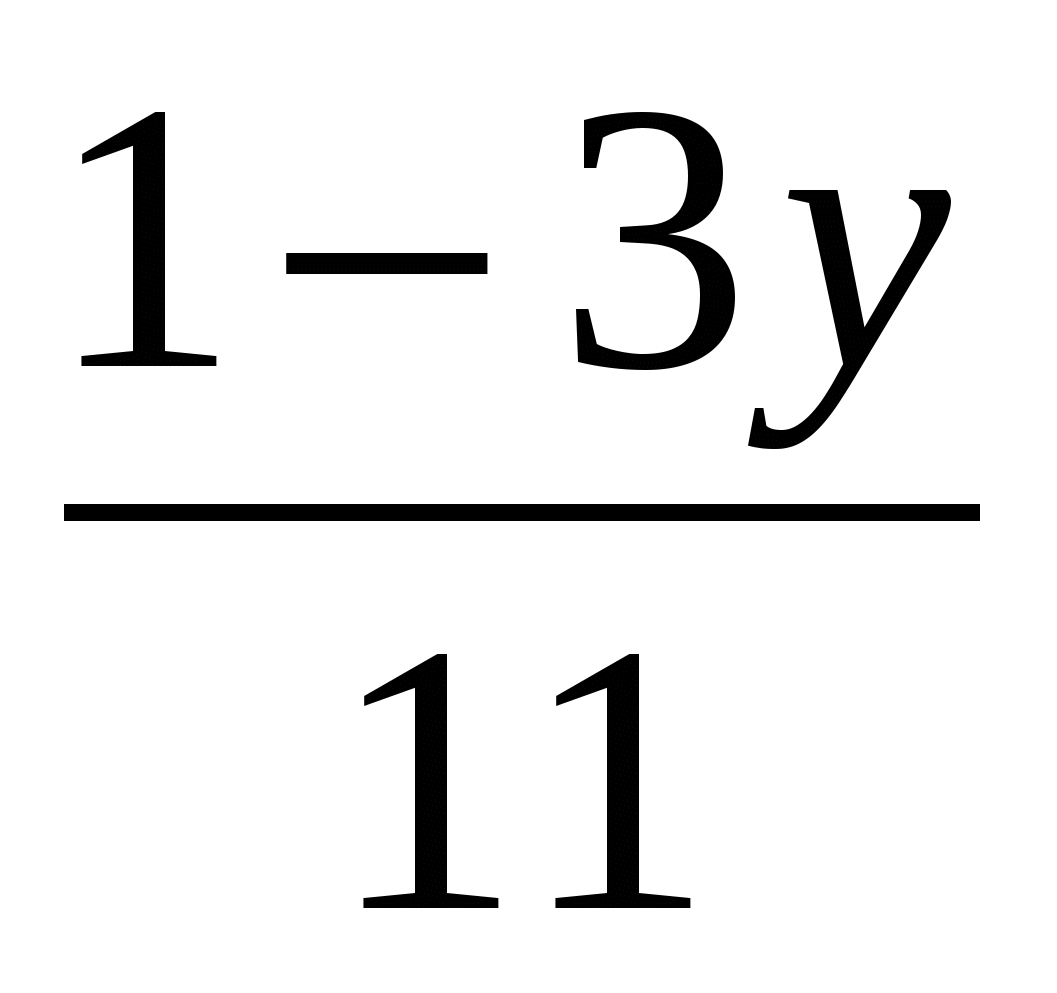 – – 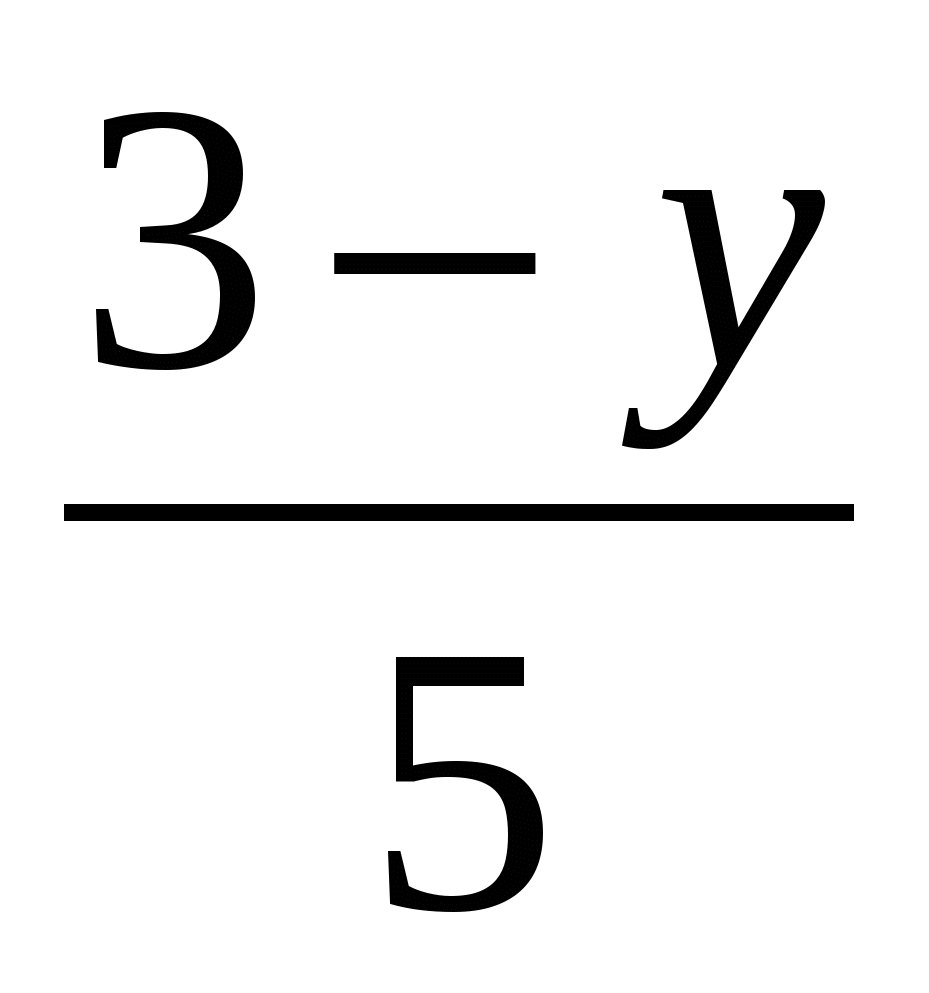 = 0, в) 9х2 – = 0, в) 9х2 – 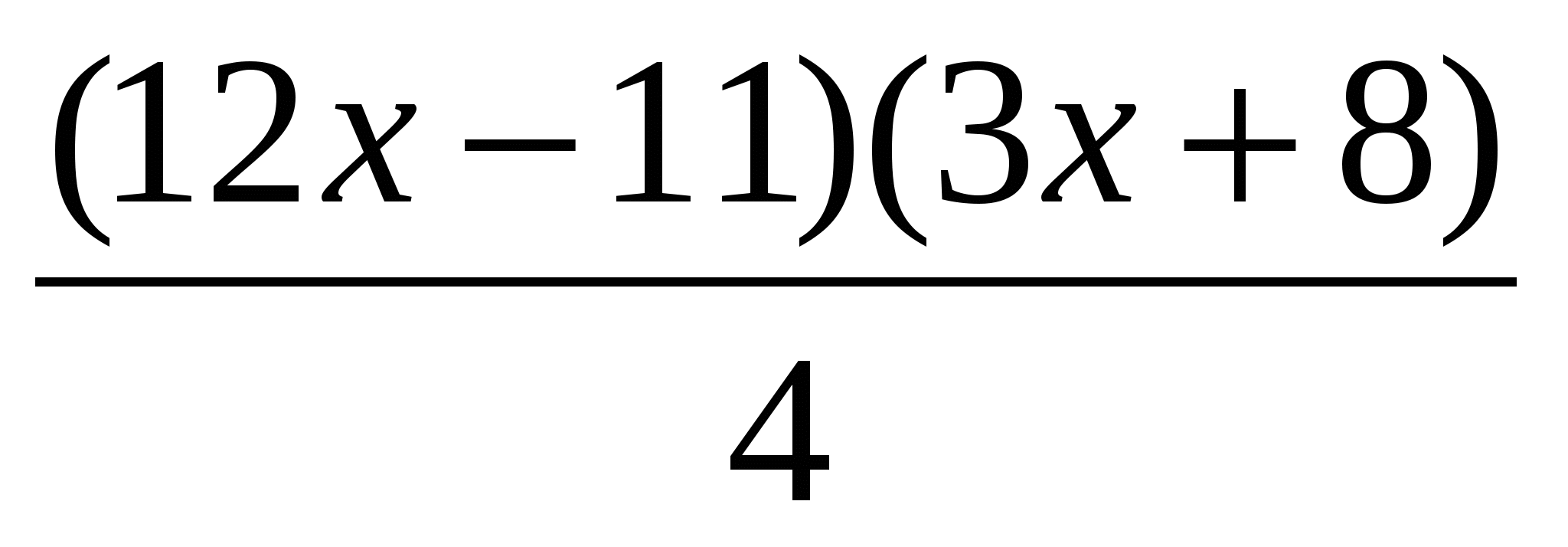 =1, =1,
36 – х2 – х2 + 11х – 36=0, 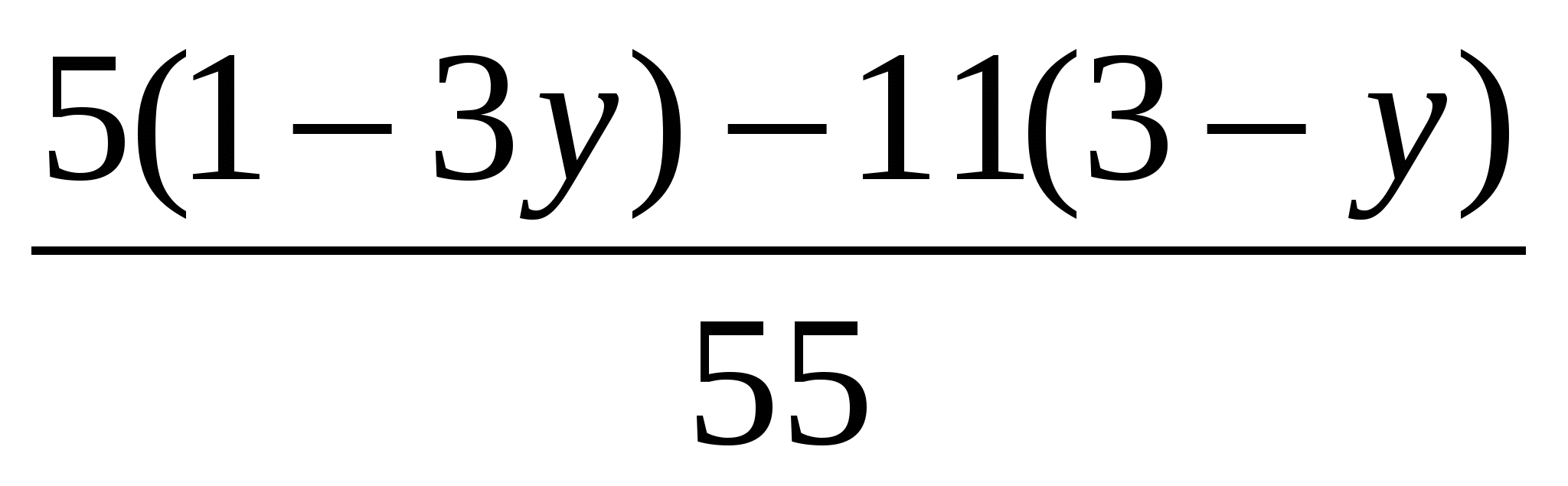 = 0, 36х2–(36х2 –33х+96–88)– 4=0 = 0, 36х2–(36х2 –33х+96–88)– 4=0
– 2х2 + 11х = 0, т.к. 55 ≠ 0, 36х2–36х2 +33х–96х+88 – 4=0
х (11 – 2х) = 0, 5 – 15у -33 + 11у = 0, – 63х = – 84,
х1 = 0 и 2х2 = 11, -4у = 28, х= 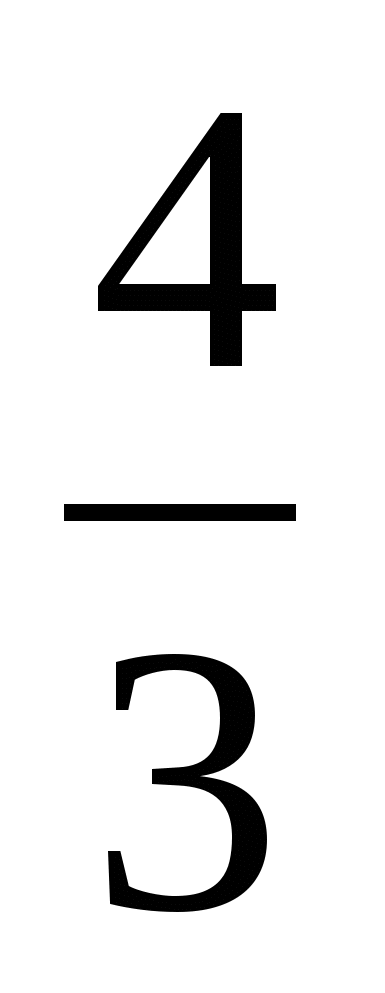 = 1 = 1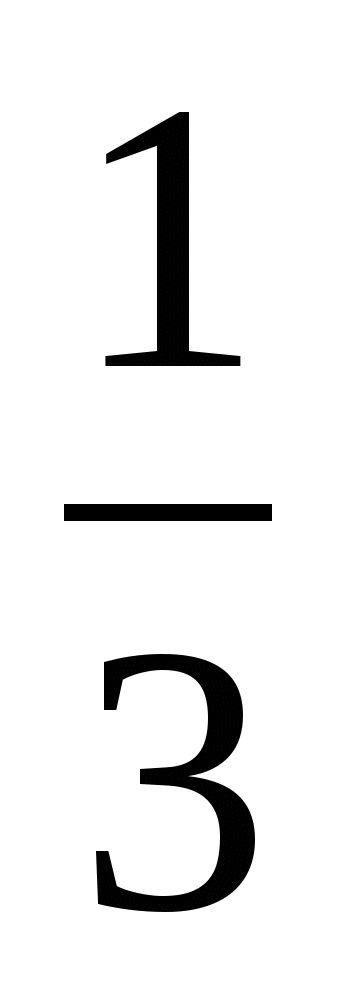
х2 = 5,5 у = –7
Ответ: 0; 5,5 Ответ: – 7 Ответ: 1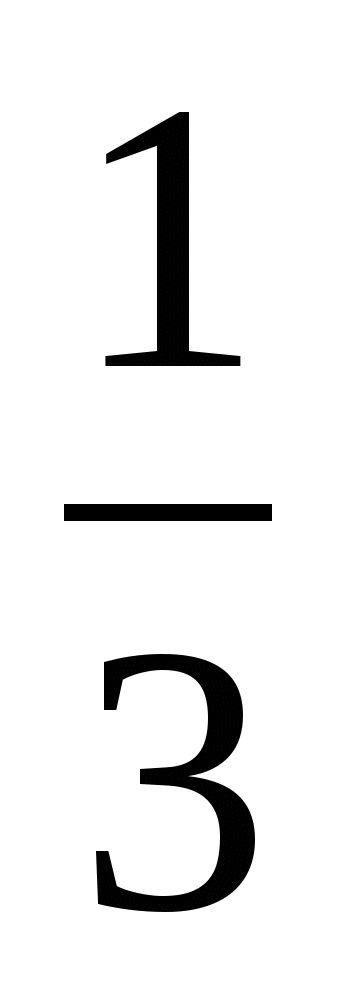 . .
Учитель: Уравнения ребята бывают 1, 2, 3, 4, и более высоких степеней. Мы с вами большей частью решаем уравнение I, II иногда III степени. Давайте решим уравнение I степени и узнаем, сколько оно может иметь корней.
(На доске): 2x-5=10, 7х= 0
Учитель: А теперь проверим. Сколько корней может иметь уравнение I степени?
Ученики: Не более одного.
Учитель: А теперь решим уравнение II степени (квадратное).
I вариант
|
II вариант
|
III вариант
|
x2-5x+6=0
|
y2-4y+7=0
|
x2-12x+36=0
|
Д=1, Д>0
|
Д=-12, Д<0
|
Д=0, 1 корень
|
x1=2, x2=3
|
нет корней
|
x=6
|
А теперь проверим. Сколько корней может иметь уравнение II степени?
Ученики: Не более двух.
Учитель: Попробуем выяснить, сколько корней может иметь уравнение III степени?
I вариант
|
II вариант
|
III вариант
|
x3-1=0
|
x3-4x=0
|
x3-12x2+36x=0
|
x3=1
|
x(x2-4)=0
|
x(x2-12x+36)=0
|
x=1
|
x=0, x=2, x= -2
|
x=0, x=6
|
1 корень
|
3 корня
|
2 корня
|
А теперь проверим. Итак, сколько корней может иметь уравнение III степени?
Ученики: Не более трёх.
Учитель: Существуют также и уравнения более высоких степеней. Это уравнения 4 степени, 5 степени. А сколько они могут иметь корней? Для решения уравнений 4, 5 и более степеней существуют специальные методы. Если будете учиться в профильном классе, то конечно научитесь решать некоторые из них.
|
Контроль
элементы волевой саморегуляции
знаково-символические действия,
умение осознанно и произвольно строить речевое высказывание в устной и письменной форме;
выбор наиболее эффективных способов решения задач в зависимости от конкретных условий;
контроль и оценка процесса и результатов деятельности;
извлечение необходимой информации из прослушанных текстов
анализ
синтез
установление причинно-следственных связей,
построение логической цепи рассуждений,
выдвижение гипотез
|
IV. Изучение нового материала 2.
Мы с вами сегодня решали уравнения аналитическим способом, но существует не только этот способ. Прежде чем с ним познакомится, вспомним известные нам функции и их графики! Из списка функций приве-денного на доске выберите функцию, соответствующую данному графику. Запишите в тетради данные соответствия/ Внимание на экран
Функции записаны на доске:
А у = – х +3 Г у = (х + 2) 2 + 5 Ж у = 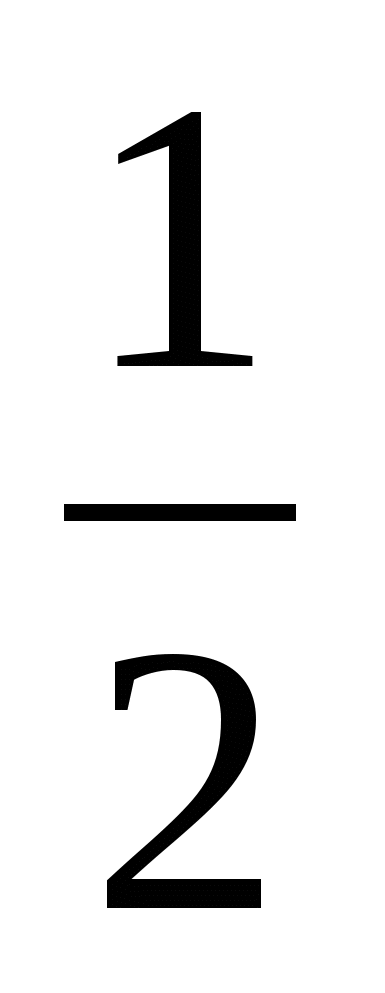 х 2+1 х 2+1
Б у = х3+3 Д у =х З у = - х 2 + 4
В у = (х – 2) 2 Е у = х 2– 2 И у = 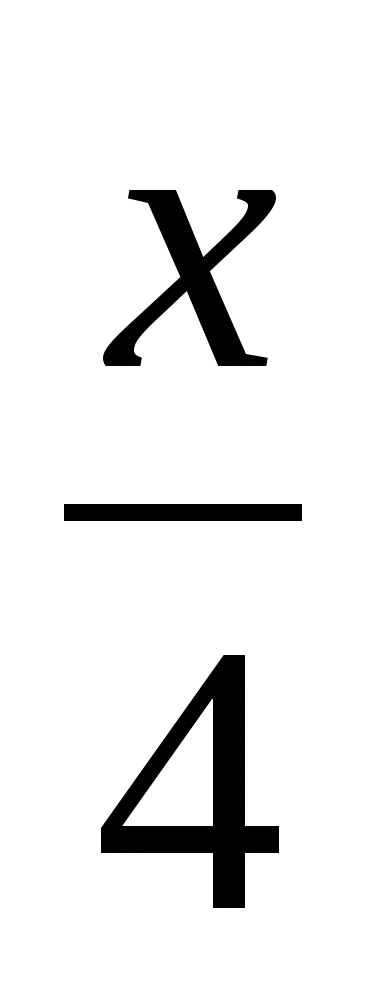
Проверьте правильность выполнения
задания своего соседа по парте
Давайте попробуем решить уравнение x3+x-4=0. А сколько корней оно может иметь?
(Ученики отвечают):
Запишем это уравнение в виде x3=-x+4. А теперь рассмотрим функции y=x3 и y=-x+4. Что является графиками данных функций?
Ученики: Кубическая парабола и прямая. ;
Учитель: Это уравнение можно решить графически. Давайте откроем учебник (Алгебра 9 класс), стр.58. На рисунке 43 нам представлены графики данных функций. Вы видите, ребята, что графики имеют точку пересечения. Попробуйте назвать корень данного уравнения.
Ученики: называют: 1,3 < х < 1,4
Учитель: Как вы думаете, в чём недостаток данного метода решения?
Ученики: Он не точен.
Учитель: Да, графический способ решения уравнений не всегда обеспечивает высокую точность результата, и поэтому иногда приходится этот результат уточнять при помощи вычислений. Итак, ребята, данное уравнение имеет 1 решение.
А если бы уравнение имело бы 2 решения, то, как бы могла прямая располагаться по отношению к кубической параболе.
(Идёт создание проблемной ситуации).
Объединитесь по группам (4 человека) и сделайте эскиз рисунка, если три решения?
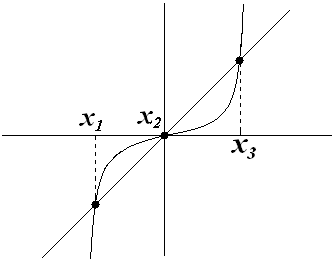
Проверили по вертушке (взаимопроверка)
|
контроль и оценка процесса и результатов деятельности;
элементы волевой саморегуляции
поиск и выделение необходимой информации
применение методов информационного поиска, в том числе с помощью компьютерных средств
знаково-символические действия, включая моделирование
умение осознанно и произвольно строить речевое высказывание в устной и письменной форме;
выбор наиболее эффективных способов решения задач в зависимости от конкретных условий;
рефлексия
смысловое чтение как осмысление цели чтения и выбор вида чтения в зависимости от цели;
определение основной и второстепенной информации;
анализ
синтез
построение логической цепи рассуждений,
умение слушать и вступать в диалог
участвовать в коллективнов обсуждение проблем
строить продуктивное взаимодействие в группе сверстников
контроль, коррекция, оценка действия партнера
|
V. Закрепление.
А сейчас рассмотрим пример решения уравнения графическим способом
Чтобы решить уравнение
х2 + 2х – 8 =0
представим его в виде
х2 = – 2х +8,
Далее рассмотрим функции
у = х2 и у = – 2х +8.
Что является графиком каждой функции?
Построим графики этих функций в одной
системе координат. Определим абсциссы
точек пересечения, они будут являться
корнями нашего уравнения
Ответ: – 4 ; 2.
|
Контроль в форме сличения способа действия с заданным эталоном
знаково-символические действия, включая моделирование
умение осознанно и произвольно строить речевое высказывание в устной и письменной форме
извлечение необходимой информации
анализ
построение логической цепи рассуждений,
|
VI. Итог урока.
Учитель: А теперь давайте, ребята обобщим то, о чём мы говорили.
- Какие уравнения мы сегодня решали?
- Какой степени они были?
- Вспомните методы решения уравнений!
- Перечислите: сколько корней может иметь целое выражение____ степени?
В конце урока задание на рефлексию
А сейчас поставьте в тетради сами себе оценку за работу на уроке.
Выставление оценок учителем
VI. Домашнее задание.
|
Анализ и синтез
умение осознанно и произвольно строить речевое высказывание в устной и письменной форме
выбор наиболее эффективных способов решения задач в зависимости от конкретных условий;
рефлексия способов и условий действия,
| |
|
|
 Скачать 87.45 Kb.
Скачать 87.45 Kb.