Урок по теме «Квадратные уравнения»
 Скачать 69.47 Kb.
|
 Урокпо теме «Квадратные уравнения» Цель урока:
Ход урока Организационный момент Учитель. Сегодня мы завершаем изучение темы «Квадратные уравнения». Цель этого урока – вспомнить способы решения квадратных уравнений различных видов, систематизировать имеющиеся знания и самостоятельно получить некоторые дополнительные формулы, облегчающие решения квадратных уравнений в некоторых особых случаях. Блиц-опрос ( фронтальный устный опрос) На доске таблица с предложенными уравнениями
а) сумму корней : х1+х2; (2) б) произведение корней: х1∙х2; (-8) в) квадрат суммы корней: ( х1 +х2)2; (4) г) удвоенное произведение корней: 2 х1∙х2; ( -16) д) значения суммы 1/х1+1/х2 ; ( -0,25) е) 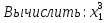 +  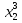( 56)Повторение Учитель. Мы уже вспомнили имя Франсуа Виета – одного из математиком, занимавшихся изучением уравнений и их классификацией. Сейчас, вспоминая основные способы решения квадратных уравнений, мы узнаем имя другого математика, жившего в Древней Греции и посвятившего решению линейных и квадратных уравнений много времени. На доске записаны квадратные уравнения и соответствующие им буквы. Отвечая на вопрос, вам нужно выбрать из предложенных такое уравнение. Которое проще решить указанным способом, назвать букву и составить слово.
Какое уравнение удобнее решать: - извлечением квадратных корней из обеих его частей? [Д] - вынесением общего множителя за скобки? [И] - представляя его в виде квадратного двучлена? [О] - используя общую формулу корней? [Ф] - по формуле, связанной с чётностью коэффициента? [А] - по теореме, обратной теореме Виета? [Н] - разложением на множители по формуле разности квадратов? [Т] Изучение нового материала
3х2+4х-5 = 0 и 3х2-4х+5 = 0. Выясните, имеют ли они корни. [1-е уравнение: да, D = 76; 2-е уравнение: нет, D = -44.]
2х2+4х-10 = 0 и -3х2+7х-8 = 0? [Разделить обе части на одно и то же число.]
Возможные результаты анализа Наблюдение 1. Все уравнения, кроме одного (№ 8), имеют корень 1 или -1. Наблюдение 2. Есть уравнения, имеющие одинаковые по модулю соответствующие коэффициенты и обладающие свойством 1. Гипотеза 1. Возможно, наличие у уравнения корня 1 или -1 зависит от его коэффициента. Гипотеза 2. Пусть дано квадратное уравнение вида ах2+bх+с = 0. Если а+b+с = 0, то х1= 1 и х2 = 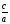 .Гипотеза 3. Пусть дано квадратное уравнение вида а+b+с = 0. Если а-b+с = 0, то х1= -1 и х2 = - 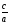 .Гипотезы 2 и 3 доказываются под руководством учителя. Самостоятельная работа Учащимся раздаются чистые листы формата А4. А. (1 мин) На лежащих перед вами листах в правом верхнем углу запишите свою фамилию и составьте 5 уравнений (не более чем с трёхзначными коэффициентами), для решения которых применяются доказанные гипотезы. Поменяйтесь листами с соседом по парте. Б. (2 мин) На полученных листах запишите в нижнем правом углу свою фамилию и решите предложенные уравнения, используя гипотезу. Сдайте листы учителю. Решение нестандартных задач
[х2-4х+1 = 0]. Задание на дом
а) х2+х = 90 в) 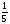 х2+х-10 = 0б) -4х = 7х2 г) х2+4х-5 = 0 2. Разность корней уравнения равна 1,5: 2х2-5х+с = 0. Найдите с. 3*. Решите уравнение двумя способами: (х+3)2-2(х+3)-8 = 0. Подведение итогов -сегодня на уроке я узнал… -сегодня на уроке я научился… -сегодня на уроке я познакомился… -сегодня на уроке я повторил… -сегодня на уроке я закрепил. Раздаточный материал
|
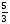
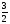
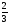
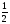
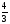
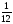
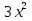/IхI -10=0 (2; -2 )
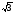и 2 -