Урок по теме «Тригонометрические функции, их свойства и графики». Певцова Ольга Евгеньевна, учитель математики

Название	Урок по теме «Тригонометрические функции, их свойства и графики». Певцова Ольга Евгеньевна, учитель математики
Дата	05.04.2016
Размер	50.15 Kb.
Тип	Урок

Алгебра и начала анализа. 10 класс.
Обобщающий урок по теме «Тригонометрические функции, их свойства и графики».

Певцова Ольга Евгеньевна, учитель математики.

Тип урока: урок применения знаний на практике.
Форма урока: урок - практикум.
Используемые технологии: дифференцированного обучения, критического мышления, коммуникативного общения, развивающее обучение.
Цели урока:

1. Развитие познавательного интереса к обучению.

2. Применение математического моделирования как способа активизации аналитического мышления.

3. Формирование практических навыков построения графиков функций на основе изученного теоретического материала.

Задачи урока:

1. Научить оперировать имеющимся потенциалом знаний по теме «Тригонометрические функции, их графики и свойства» в конкретной ситуации.

2. Закрепить основные методы построения графиков тригонометрических функций, предупредить появление типичных ошибок, подготовить к контрольной работе.

3. Научить применять осознанное установление связей между аналитической и геометрической моделями тригонометрических функций.

4. Предоставить каждому учащемуся возможность проверить свои знания и повысить их уровень.

5. Вовлечь учащихся в активную практическую деятельность.

6. Воспитывать у учащихся познавательную активность, чувство ответственности, уважения друг к другу, взаимопонимания, взаимоподдержки, уверенности в себе; культуру общения.
Ход урока.

Организационный момент.

«Вход в урок».

На доске написаны 3 утверждения:

Тригонометрические уравнения sin x = a, cos x = a, tg x = a, ctg x = a всегда имеют решения.
График тригонометрической функции у = f(-x) можно получить из графика функции у = f(x) только с помощью преобразования симметрии относительно оси Оу.
График гармонического колебания можно построить, используя одну главную полуволну.

Учащиеся обсуждают в парах: верны ли утверждения? (1 минута). Затем результаты первоначального обсуждения (да, нет) вносятся в таблицу в столбец «До».

Утверждение	До	После
1
2
3

Учитель ставит цели и задачи урока.

Устные упражнения (фронтально).

1) Проверьте, принадлежат ли точки графикам функций:

у = sin x точка с координатами (π; 0),

у = cos x точка с координатами (

; 1).

2) Найти наибольшее и наименьшее значения функций:

у = sin x на отрезке

,

у = cos x на полуинтервале

,

у = tg х на полуинтервале

.

3) Решите уравнения: cos x = 0, tg х = -1, sin x = 2.

4) Является ли число 15π периодом функций: у = sin x, у = cos x, у = tg х?

Назовите основной период этих функций.

5) Используя рисунки 14-17 на странице 38 задачника, составить аналитические модели функций по графикам.

Разминка (самостоятельно, с проверкой за доской).

№ 216(б). Решите графически уравнение sin x + cos x = 0.

5. Практическая работа № 1 (работа на заготовленных макетах в 4 группах, группы составлены по уровню подготовленности учащихся).

1 группа. № 210 (г). Сколько решений имеет система уравнений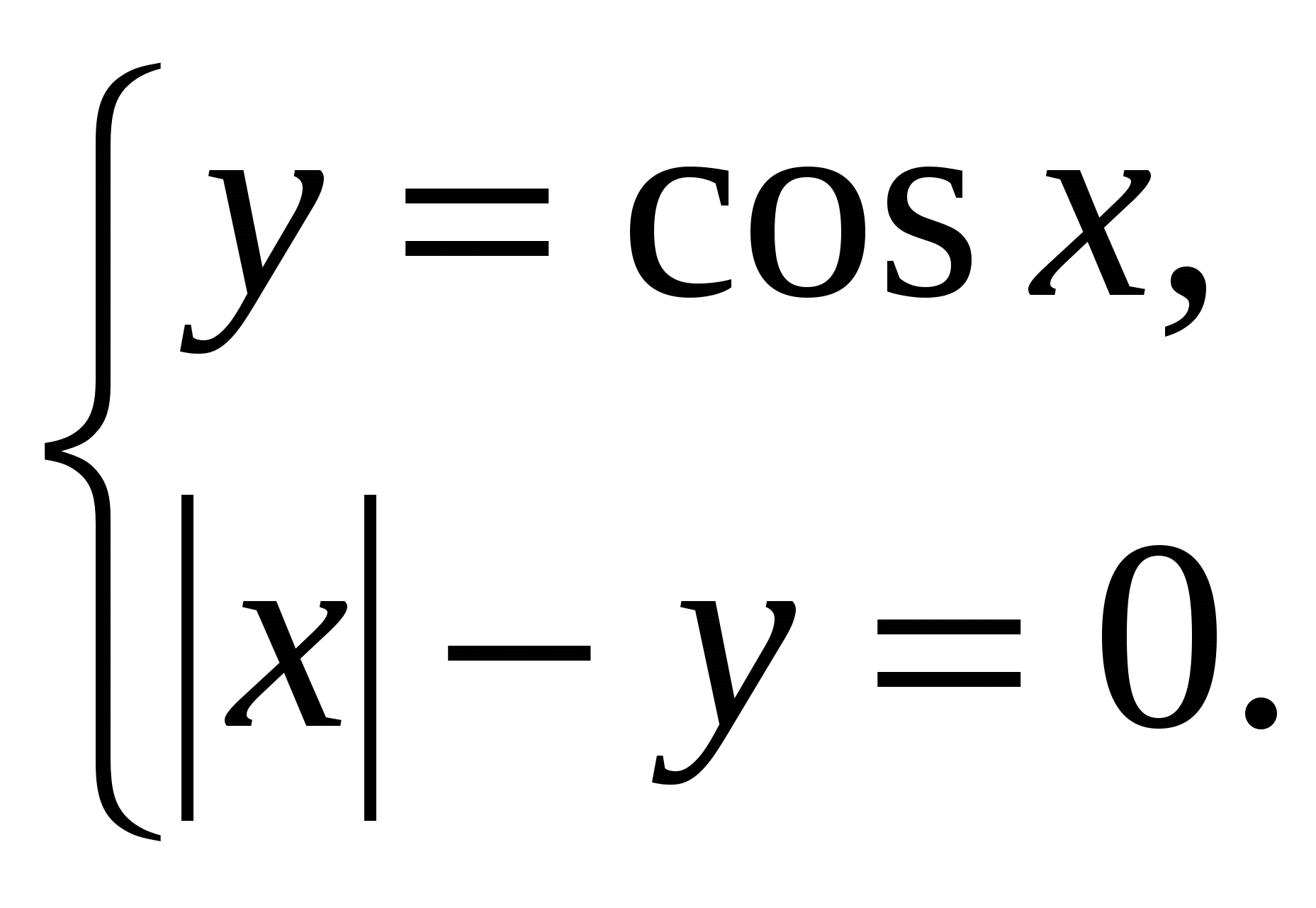

2 группа. № 183 (б). Решите графически уравнение sin x = х² + 1.
3 группа. № 209 (в). Решите графически уравнение cos x = - (х – π)² – 1.

4 группа. Сколько решений имеет уравнение sin 2x = tg х на отрезке

.

(Проверка и обсуждение по макетам).

Практическая работа № 2 (самостоятельная работа на листочках, 4 варианта, задания составлены по уровню подготовленности учащихся).

Построить график функции:

1 вариант. у = 2 sin x – 1.

2 вариант. у = 3 cos

.

3 вариант. у = 2 sin (-2x).

4 вариант. у =

cos 3

.

7. Обобщение и подведение итогов.

№ 194 (б,в). Постройте и прочитайте график функции у = f(x), где

f(x) =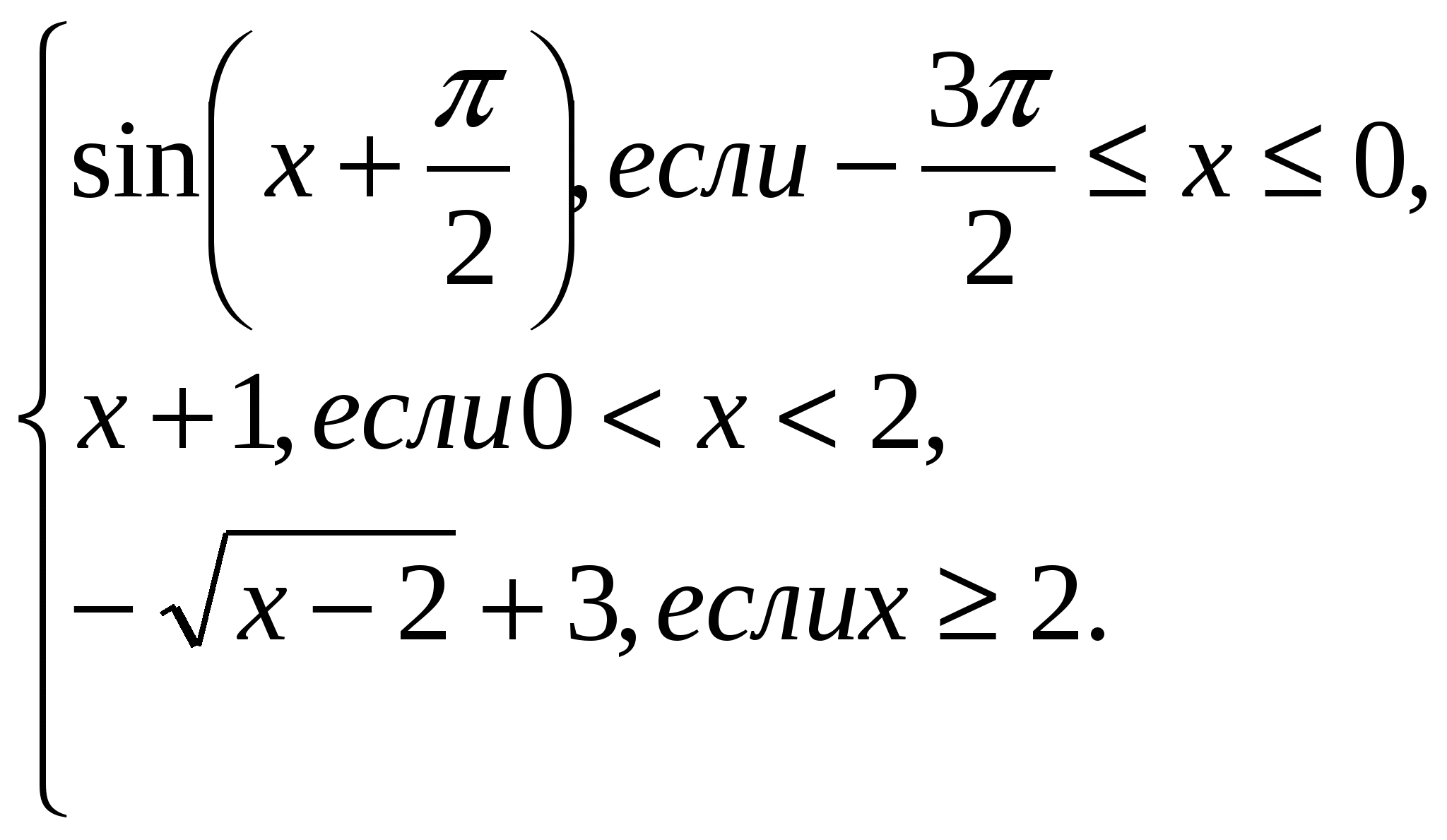

8. Итог урока. Возвращаемся к утверждениям (начало урока), обсуждаем, используя свойства тригонометрических функций, и заполняем в таблице столбец «После».

Учитель анализирует ход урока и его основные моменты, выборочно оценивает деятельность учащихся на уроке. Дает домашнее задание для подготовки к контрольной работе.

В работе используется УМК А.Г.Мордковича «Алгебра и начала анализа 10-11 класс», в котором основной содержательно-методической линией выбрана функционально-графическая. Это выражается, прежде всего, в том, что построение материала практически всегда осуществляется по жесткой схеме: функция – уравнения – преобразования. Тригонометрические функции являются первыми трансцендентными функциями, изучаемыми в школьном курсе математики. Их роль и место определяются главным образом двумя сторонами применения этих функций в теории и практике. Во-первых, тригонометрические функции дают замечательный вычислительный аппарат для решения разнообразнейших геометрических задач. Во-вторых, учение о тригонометрических функциях позволяет весьма наглядно, просто и убедительно продемонстрировать важнейшие свойства функций: периодичность, четность и нечетность, ограниченность, монотонность и т.д. и научиться применять их при решении тригонометрических уравнений, неравенств и систем уравнений.

Применение свойств тригонометрических функций для решения уравнений и неравенств является привычной частью вариантов выпускных и вступительных экзаменов, вариантов ЕГЭ, их широкий набор представлен и в пособиях для поступающих в вузы. Поэтому учащиеся с интересом относятся к изучаемой теме.

Анализ контрольной работы по данной теме показал, что материал, в основном, усвоен. Трудности для некоторых учащихся вызывают построение графиков гармонических колебаний и решение более сложных уравнений графическим методом.

Певцова О.Е. Обобщающий урок по теме «Тригонометрические функции, их свойства и графики» (10 класс). Используется УМК А.Г.Мордковича «Алгебра и начала анализа 10-11 класс», в котором основной содержательно-методической линией выбрана функционально-графическая. Это выражается, прежде всего, в том, что построение материала практически всегда осуществляется по жесткой схеме: функция – уравнения – преобразования, что способствует реализации развивающей концепции математического моделирования.