Урок алгебры в 9 классе по теме "Разложение многочлена на множители с помощью комбинации различных приемов" Учитель математики
 Скачать 94.9 Kb. Скачать 94.9 Kb.
|
| Государственное бюджетное образовательное учреждение Средняя общеобразовательная школа № 466 Курортного района Санкт-Петербурга Урок алгебры в 9 классе по теме "Разложение многочлена на множители с помощью комбинации различных приемов" Учитель математики Хамина Ирина Анатольевна Санкт-Петербург 2013 Цели урока: 1.Систематизировать, расширить и углубить знания, умения учащихся применять различные способы разложения многочлена на множители и их комбинации. 2.Способствовать развитию наблюдательности, умения анализировать, сравнивать и делать выводы. Оборудование: проектор, магнитная доска, набор карточек с заданиями теста, индивидуальные оценочные листы, копировальная бумага. Ход урока: Работа учащихся состоит из трех этапов. Результаты каждого этапа урока ученики заносят в индивидуальные оценочные листы:
Оценка за урок зависит от суммы n набранных баллов по всем заданиям. Если n Этап 1. Начало урока посвящается повторению: выполнение трех заданий, демонстрация характеристик приемов разложения многочлена на множители. В парах выполняется задания 1 на карточках. Карточка №1. 1. Разложение многочлена на множители – это А. Представление многочлена в виде суммы двух или нескольких многочленов. Б. Представление многочлена в виде произведения двух или нескольких одночленов. В. Представление многочлена в виде произведения двух или нескольких многочленов. Оценка – 2 балла. (Ответ: в) 2. Завершить утверждение: Представление многочлена в виде произведения одночлена и многочлена называется … Оценка – 2 балла. (Ответ: вынесением общего множителя за скобки) 3. Восстановить порядок выполнение действий при разложении многочлена на множители способом группировки. 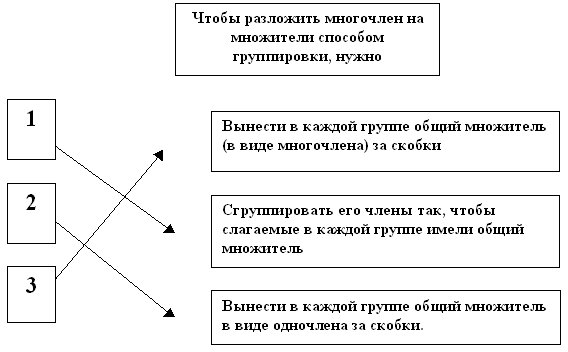 Оценка-3 балла. 4. Отметить знаком “+” верные утверждения. 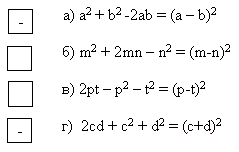 Оценка – 4 балла (по 1 баллу за каждое верно выбранное и верно невыбранное выражение). Учитель включает проектор и демонстрирует слайд с ответами к заданиям карточки. Происходит быстрая проверка и комментарий заданий. Учитывая коэффициент участия в работе, ученики распределяют между собой заработанное количество баллов, выставляют их в оценочные листы. Затем на магнитной доске двое учеников выполняют второе задание 2. Его суть – провести классификацию данных многочленов по способу разложения на множители. В результате ученики собирают таблицу: 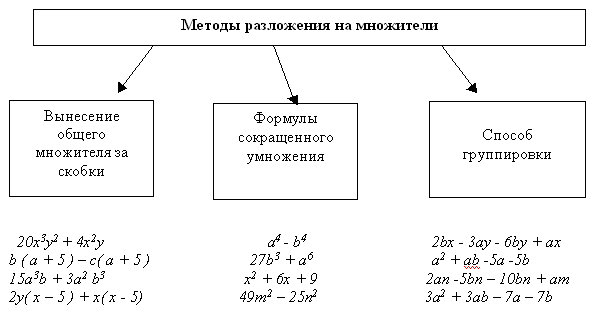 Остальные учащиеся собирают математическое лото. Математическое лото представляет собой две карточки. Одна имеет рисунок с лицевой стороны, а с изнаночной – ответы на задания, она разрезается на квадраты. На второй карточке задания, которые решают и подобный ответ ищут на первой карточке, накладывая изнаночной стороной на вторую карточку. В результате получится рисунок. Карточка с заданиями:
Карточка с ответами (разрезная, изнаночная сторона):
После выполнения работы пары получают рисунки, производят взаимопроверку, рассматривают работу учеников у доски. Оценка – 9 баллов ( по1 баллу за каждое верное составление ). Затем проверяется задание: учащиеся поясняют, почему многочлены можно разложить на множители, используя данные методы разложения. Оценка – 12 баллов (по 1 баллу за каждое верное составление). Даем характеристику перечисленному приему, демонстрируя слайды.
Этап 2. На практике при решении примеров часто приходится использовать комбинацию различных приемов. Поэтому, чтобы успешно решать такие примеры сегодня, мы попытаемся выработать план их последовательного применения. Иными словами, здесь нужны не только знания, но и опыт. Задание 3. Разложите многочлен на множители и укажите какие приемы использовались при этом. У доски одни и те же примеры выполняют три учащихся с последующей проверкой правильности выполнения учащимися класса. Пример 1. 36 a6 b3 – 96a4 b4 + 64a2b5 Решение: 36 a6 b3 – 96a4 b4 + 64a2b5 = 4a2b3(9a4 – 24a2 b + 16b2) = 4a2b3(3a2 – 4b)2. Комбинировали два приема: – вынесение общего множители за скобки; – использование формул сокращенного умножения. Пример 2. a2 + 2a b + b2 – c2 Решение: a2 + 2a b + b2 – c2 = (a2 + 2a b + b2) – c2 = (a + b)2 – c2= ( a + b – c ) ( a + b + c ) Комбинировали два приема: – группировку; – использование формул сокращенного умножения. Пример 3. y3 – 3y2 + 6y – 8. Решение: y3 – 3y2 + 6y – 8 = ( y3 – 8 ) – ( 3y2 -6y ) = ( y -2 ) ( y2 + 2y + 4 ) – 3y( y – 2 )= ( y – 2)( y2 + 2y + 4 – 3y )= ( y – 2)( y2 – y + 4 )/ Комбинировали три приема: – группировку; – вынесение общего множителя за скобки; – использование формул сокращенного умножения. Эти примеры показывают, что при разложении многочлена на множители полезно соблюдать следующий порядок ( демонстрация слайда):
Пример 4. n3 + 3n2 + 2n. Решение: n3 + 3n2 + 2n = n ( n2 + 3n + 2 ) = n ( n2 + 2n + n + 2 ) = n (( n2 + 2n ) + ( n + 2 )) = n ( n ( n + 2 ) + n + 2 ) = n ( n + 1 ) ( n + 2 ). Комбинировали три приема: – вынесение общего множителя за скобки; – предварительное преобразование; – группировку. Отмечаем, что для решения этого примера мы использовали еще один прием разложения на множители – предварительное преобразование. Даем ему характеристику (демонстрация слайда):
Оценка – 4 балла ( по1 баллу за каждый правильно, самостоятельно решенный пример ). Задание 4. Совокупность различных приемов разложения многочленов на множители позволяет легко и изящно производить не только арифметические вычисления, но и решать уравнения вида ax2 + bx + c = 0 , где 1. Решить уравнение: x2 + 10x + 21 = 0 Решение: x2 + 10x + 21 = 0 x2 + 10x +25 – 4 = 0 ( x + 5 )2 – 4 = 0 ( x + 5 – 2 ) ( x + 5 + 2 ) = 0 ( x + 3 ) ( x + 7 ) = 0 x + 3 = 0 или x + 7 = 0 x = – 3 или x = – 7 Ответ: – 7; – 3. Отмечаем, что при разложении многочлена на множители мы “увидели” полный квадрат (x2 + 10x +25 = ( x + 5 )2) и таким образом применили еще один прием разложение многочлена на множители : метод выделения полного квадрата. 2. Доказать, что при любом натуральном n значение выражения ( 3n – 4 )2 – n2 кратно 8. Решение: (3n – 4 )2 – n2= ( 3n – 4 – n) ( 3n – 4 + n ) = ( 2n – 4 ) ( 4n – 4 ) = 8 (n – 2 (n – 1). Так как в полученном произведении один множитель делится на 8, то все произведение делится на 8. 3. Вычислить Решение: 4. Доказать тождество ( a2 + 3a )2 + 2 ( a2 + 3a )=a ( a + 1)( a +2 )( a + 3 ). Преобразуем левую часть равенства в правую. ( a2 + 3a )2 + 2 ( a2 + 3a ) = ( a2 + 3a )( a2 + 3a + 2 ) = a ( a + 3)( a ( a + 2 ) + ( a + 2 ))= a ( a + 3 )( a + 2 )( a + 1 ) = a ( a + 1 )( a + 2 )( a + 3 ). Ч.т.д. Оценка – 4 балла ( по1 баллу за каждое правильное решение). Этап 3. Задание 5. Самостоятельная работа (на листочках под копирку).
Самостоятельная работа проверяется на уроке с помощью проектора. Копии решений сдаются учителю, осуществляют самопроверку и самооценку знаний. Отметка за работу равна числу верно выполненных заданий. Слайд с ответами к заданиям.
Оценка – 5 балла ( по1 баллу за каждое правильное решение). Подведение итогов урока. Учащиеся проставляют количество баллов в оценочный лист. Оценивают свою работу на уроке. Учитель проводит фронтальный обзор основных этапов урока; отмечает, что кроме трех основных приемов разложения на множители: вынесение общего множителя за скобки, группировки, использование формул сокращенного умножения , – учащиеся познакомились еще с двумя способами: методом выделения полного квадрата, предварительным преобразованием; оценивает работу учащихся и ориентирует учеников в домашнем задании. Домашнее задание. Если вы получили оценку: “5” – № 658 (в, г); “4” – № 650; “3” – № 642 (в), № 645 (в), № 649 (в); “2” – № 640 (б), № 642 (а), № 644 (г). | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||