Урок алгебры Квадратный корень из дроби 8 класс Автор-составитель: учитель математики Пятышева А. И
 Скачать 73.17 Kb.
|
ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕСРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА № 152КРАСНОГВАРДЕЙСКОГО РАЙОНА САНКТ-ПЕТЕРБУРГАУрок алгебры Квадратный корень из дроби 8 класс Автор-составитель: учитель математики Пятышева А.И. Данный урок в 8 классе является уроком изучения нового материала при изучении темы «Квадратные корни». К этому уроку обучающиеся знают определения квадратного корня и арифметического квадратного корня, свойства квадратного корня из степени и произведения. Обучение алгебре реализуется по учебно-методическому комплекту (УМК) «Алгебра» (авторы: Ш.А. Алимов, Ю.М. Колягин, Ю.В. Сидоров и др.) предназначен для 8 классов общеобразовательных учреждений. Тип урока: урок изучения нового материала. Оборудование, используемое на уроке: компьютер, мультимедийный проектор, Цифровые ресурсы: презентация, разработанная в среде PowerPoint Литература, используемая при подготовке к уроку:
Образовательные технологии: на уроке используются элементы информационно-коммуникационных технологий, технологий обучения в сотрудничестве. Формы работы учащихся: групповая и фронтальная при решении тренировочных задач (с доской и в индивидуальных карточках), индивидуальная по карточкам, устная работа для актуализации знаний обучающихся. Универсальные учебные действия, развитие и формирование которых осуществляется в рамках урока: Регулятивные учебные действия обеспечивают возможность управления познавательной и учебной деятельностью посредством постановки целей, планирования, контроля, коррекции своих действий, оценки успешности усвоения. Личностные действия позволяют сделать учение осмысленным, увязывая их с реальными жизненными целями и ситуациями (самоопределение, нравственно-эстетическое оценивание). Познавательные действия включают действия исследования, поиска, отбора и структурирования необходимой информации, моделирование изучаемого содержания (общеучебные универсальные действия, логические универсальные действия, постановка и решение проблемы). Коммуникативные действия обеспечивают возможности сотрудничества: умение слышать, слушать и понимать партнера, планировать и согласованно выполнять совместную деятельность, распределять роли, взаимно контролировать действия друг друга, уметь договариваться, вести дискуссию, правильно выражать свои мысли, оказывать поддержку друг другу и эффективно сотрудничать как с учителем, так и со сверстниками. Цель урока: сформулировать и доказать теорему о квадратном корне из дроби, формировать умение применять это свойство квадратных корней для преобразования выражений. Задачи: - обучающие - повторить понятия квадратного корня и арифметического квадратного корня, свойства арифметического квадратного корня; формировать умения применять эти свойства. - развивающие - развивать мыслительные операции (проведение аналогии, анализ, синтез); развивать вычислительные навыки; развивать логическое мышление. - воспитательные - развивать интерес к математике, воспитывать активность и творческое отношение к работе на уроке. План урока
Ход урока.
Приветствие учащихся. Проверка готовности к уроку. Слайд1.
Какую большую тему мы изучаем? На предыдущих уроках мы рассмотрели некоторые свойства квадратного корня и сегодня познакомимся еще с одним. Слайд 2. Тема урока: «Квадратный корень из дроби» и мы должны реализовать следующие цели: - сформулировать и доказать теорему о корне из дроби; - учиться применять это свойство для преобразования выражений. Вы знаете, что через несколько месяцев в нашей стране начнется грандиозное событие мирового уровня – Олимпиада в Сочи. Сегодня наш урок, так или иначе, будет связан со спортом.
Но начнем мы с проверки домашнего задания. Тест. Слайд 3. Вопросы детей.
Перед важным стартом любой спортсмен проводит разминку, и мы сегодня не исключение, только она у нас будет математическая. - дайте определение квадратного корня - дайте определение арифметического квадратного корня - как называется символ арифметического квадратного корня? - чему равен квадратный корень из степени? - чему равен квадратный корень из произведения? 1) устный счет: слайды 5, 6, 7, 8, 9, 10 а) используя определение квадратного корня вычислить:  ; ; ;  ;б) табличные значения:  ;  ; ; ; ; ;  ;в) квадратный корень из произведения  ; ; ; ;г) квадратный корень из степени;  ; ; ; ;  ; д) вынести множитель из-под знака корня:  ; ;  ; .е     ) внести множитель под знак корня:
Для успешного выступления на соревнованиях, спортсмены не только тренируются, но еще изучают теоретический материал: например: технику полета или скольжения, тактику игры, состав смазки, правильное питание и т.д. Мы тоже должны рассмотреть теоретический материал, чтобы применять его в упражнениях. Написать задание для учащихся на доске по вариантам «вычислить квадратный корень из дроби»: Вариант 1:  = Вариант 2:  =Если учащиеся выполнили первое задание: спросить, как они его сделали? 1 вариант: представили в виде квадрата  и получили  . Сделать вывод. 2 вариант: представили числитель и знаменатель используя определение степени в виде  и получили .Какой вывод можно сделать? Провести аналогию записать в буквенном виде:  Ввести теорему. Теорема. Если  и b > 0, то корень из дроби равен корню из числителя, деленному на корень из знаменателя.Предложить учащимся провести доказательство Докажем, что 1)  Так как  и 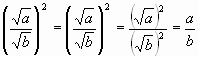 > 0, то 2)   Рассмотреть пример, предложить учащимся решить его.  Сделать вывод: при делении корней можно разделить подкоренные выражения и из результата извлечь корень.  Задание: придумать свой пример на обе формулы. Посмотреть теоретический материал в учебнике стр.100
Разминку мы провели, теоретический материал изучили, пора приступать к тренировке. Устная работа № 362 Работа у доски №363-365 (четные) А сейчас мы проведем первые небольшие соревнования Самостоятельная работа обучающего характера. Слайд 11. Предложить учащимся, кто хорошо понял тему 3 вариант. (взаимопроверка результатов) 1 вариант 2 вариант а) Вычислите значение корня:   b) Найдите значение выражения:   c) Найдите значение выражения, заменяя смешанное число дробью:   3 вариант Найдите значение выражения:  Взаимопроверка. Слайд 12. - Обменяйтесь тетрадями с соседом по парте, оцените работу и поставьте оценку. Критерии оценки: «5» - 6 верно решённых примеров «4» - 5 верно решённых примеров «3» - 4 верно решённых примеров -Поднимите руки, кто получил «4» или «5»?
-С какой теоремой познакомились на уроке? -Чему учились на уроке? Выставление оценок за урок. Шёл мудрец, а навстречу ему три человека, которые везли под горячим солнцем тележки с камнями для строительства храма. Мудрец остановился и задал каждому по вопросу. У первого спросил: «Что ты делал сегодня?» И тот с ухмылкой ответил, что целый день возил проклятые камни. У второго мудрец спросил: «А что ты делал сегодня?» и тот ответил: «А я добросовестно выполнял свою работу». А третий улыбнулся, его лицо засветилось радостью и удовольствием. А я принимал участие в строительстве храма. - Ребята, кто работал так, как первый человек? - Кто работал как второй человек? - Кто принимал участие в строительстве храма? |