Учебного материала для подготовки слабоуспевающих учащихся к егэ по математике на основе поэтапного развития метапредметных и предметных умений
 Скачать 142.85 Kb.
|
| Отбор и подача учебного материала для подготовки слабоуспевающих учащихся к ЕГЭ по математике на основе поэтапного развития метапредметных и предметных умений Из банка заданий ЕГЭ по математике сформированы карточки по 4-6 заданий вида: В1, В2, В3, В4, В5, В8. Таким образом, 40 карточек для индивидуальной работы содержат в общей сложности полторы сотни задач. Все отобранные типовые задачи разбиты на пять учебных уровней сложностей. Уровень 1 – элементарный состоит из восьми тестов, состоящих из четырех задач вида: В2, В4, В1, В5. Причем, в поле условия каждой задачи 1-го уровня была нарисована сетка ответов части В, чтобы отработать правильность записи ответа соответствующим образом. В первый уровень сложности были отобраны самые простые расчетные задачи, не содержащие многозначных чисел, дробей, процентов, дополнительных условий. Для формирования умения разделять текст сюжетной задачи на «дано» и «найти», составителями тестов специально заранее были выделены и подчеркнуты все ключевые слова и числовые данные, предполагая, что учитель при разборе задач с учеником будет еще и интонировать на подчеркнутых словах текста. Тест уровня 1
Последовательность подачи задач в тесте согласуется с принципом «от простой к сложной», в сравнении друг с другом. Все восемь вариантов уровня 1 сбалансированы дозированным усложнением той или иной задачи варианта (изменением содержания текстовой задачи В1, В5, увеличением числа арифметических действий для нахождения площади фигуры в В2). Таким образом, возможные отличия аналогичных задач, усложнение каждой задачи в варианте, влечет незначительное усложнение самого варианта в целом. То есть, к 8-му варианту первого уровня учащийся уже может составить представление о том, что при решении задач В1 возможно округление с избытком и с недостатком; что в В2 бывают вопросы, ответы на которые следует искать на горизонтальной оси, а бывают и – на вертикальной; в В5 – расчетные задачи бывают на самую дешевую транспортировку или на самую дорогую закупку. В целом, в каждой карточке, не смотря на ее компактность, предусмотрено пустое поле для кратких записей решения (сверху, снизу, по бокам). В этом случае тесты для каждого учащегося - индивидуальны, как и персональный вариант КИМа ЕГЭ. Это значит, что учащийся должен уметь подчеркивать, обводить, вписывать промежуточные расчеты в текстах условий. Правильные привычки и полезный опыт проговаривания, подчеркивания, прописывания и интонирования позволяет выработать внешнюю защиту для профилактики типичных ошибок, связанных с невниманием, усталостью, рассеянностью, забывчивостью, отсутствием умений концентрироваться и организовывать свои действия. Предполагается обязательное объяснение учителем ученику следующих универсальных приемов (через демонстрацию их эффективности): В задаче В2 выделять подчеркиванием в самом тексте условий и вопроса, обводить, дорисовывать нужные точки, интервалы, числовые значения на предлагаемом графике. В задаче В4 на нахождение площади заштрихованной фигуры обязательно прорисовать прямоугольный лист бумаги в клеточку, из которого «обрезанием» прямоугольных фигур возможно получение исходной. Затем, в каждом «удаляемом» треугольнике следует подписать длины катетов (число клеток вдоль сторон), и только после этого, внутрь каждого «удаляемого» треугольника вписать вычисленную его площадь. При этом, не выходя из текста задачи, рядом, на пустом поле могут производится промежуточные расчеты. Для того, чтобы в уровне 1 иметь возможность сконцентрироваться именно на обучении развертыванию внешних (универсальных) действий, необходимо было в тесты отобрать простой, с точки зрения математики, учебный материал, ограничиться удобными для счета числами. Это значит, что все подобранные задачи могут быть решены прикидкой, несложными устными расчетами. Опыт наблюдений за объяснениями учителей и анализ ошибок их учеников демонстрируют неэффективность многочасового прорешивания задач В1 о закупке сырков по 6 руб 70 коп на имеющиеся 50 рублей делением числа 50 на 6,7 в столбик. Подобный способ решения эффективен в случае, если деление в столбик у учащегося действительно является навыком, то есть производится безошибочно. Но если навыка нет, то - есть ошибки в счете. В противовес этому решение практических задач бытовой прикидкой опирается на уже имеющийся жизненный опыт подсчетов, то есть на навык. Для «прививки от стереотипов» в варианты уровня 1 специально отобраны задачи В1 с противоположным округлением (с избытком и недостатком). Пример 1. Сырок стоит 6 рублей 70 копеек. Какое наибольшее число сырков можно купить на 50 рублей? Решение: 1) типичное для 11 класса: 50/6,5=500/65≈7,69 (сырков) 2) типичное для 6 класса: 50 (рублей)=6,5 (рубля) 7 (сырков)+4,5 (сырка). 7,69≈7 сырков, так как купить 7,69 сырка невозможно, то есть, 50 рублей хватает только на 7 целых сырков. 3) прикидкой: Пара сырков стоит 13 рублей. Четыре сырка уже будут стоить 26 руб, значит восемь 52 руб. Для восьми сырков не хватает всего 2 руб для имеющихся 50 руб. Если из 52 руб вычесть стоимость одного сырка 6 руб 50 коп, то это число уже будет меньше 50 руб. Из рассуждений понятно, что на семь сырков 50 рублей хватит, а на восемь - нет. Значит, 7 сырков по данной цене – это и есть наибольшее количество их закупки на имеющуюся сумму. Ответ: 7 Пример 2: Каждый день во время конференции расходуется 90 пакетиков чая. Конференция длится 7 дней. Чай продается в пачках по 100 пакетиков. Сколько пачек нужно купить на все дни конференции? Решение: 1) типичное для школы: 90·7=630 пакетиков чая понадобиться на все 7 дней конференции 630:100=6,3 пачки чая необходимо на 8 дней конференции. Другими словами: 630 (пакетиков)=100 (пакетиков)·6 (пачек)+30 (пакетиков). Округлим с избытком до 7 целых пачек. 2) прикидкой: в первый день с одной пачки остается 10 пакетиков с одной пачки. Так как конференция длится семь дней, то открывая каждый день новую пачку, общая сумма остатков чая в конце предпоследнего шестого дня составит всего 60 пакетиков, что не обеспечит потребности конференции в последний седьмой день. Поэтому, придется докупить седьмую пачку, чтобы дополнить 60 имеющихся пакетиков до требуемых 90. Ответ: 7 Тесты уровня 2 уже состоят из пяти задач. К четырем расчетным задачам уровня 1 добавляется В5 на решение элементарного уравнения, сводящегося к линейному или элементарному квадратному (без вычисления дискриминанта, без приобретения и потери корней). Во втором уровне уже нет в самих заданиях поля записи ответов, ключевые слова задачи так же выделяются, как и в уровне 1. Тест уровня 2.
Условия задач В2 второго уровня представлены столбчатыми диаграммами. Задача В4 заменена на нахождение все тех же площадей многоугольников, но уже в координатной плоскости. Предполагается, что учащиеся будут сводить задачу к знакомому подсчету клеток, либо перерисовывать данный рисунок на лист в клетку (на ЕГЭ в бланк части С), либо дорисовывть недостающие линии в самом рисунке условия. Задания В1 практически не отличаются от элементарных формулировок задач В1 первого уровня, но уже содержат задачи на осмысление современных приемов торговли, типа «две покупаешь, третья - в подарок». Задача В5 уровня 2 усложняется введением задач с дополнительными условиями, но не предполагающих расчет процентов. Тесты третьего уровня так же, как и во втором уровне, состоят из тех же пяти задач, но условия задач в них усложняются следующим образом. В задачах В1 от ученика требуется жизненный опыт современного человека и умение перевода единиц измерения (км, кг, ч). В задачах В3 уже включены иррациональные уравнения, но сводящиеся к уравнениям вида В3 уровня 2. Существенным усложнением в уровне 3 можно считать включение в тесты задач В2 с графиками физических непрерывных процессов. Эти задачи, по понятным причинам, нельзя было включать в тесты первых двух уровней, а в уровнях 4 и 5 предусматривается отработка решения задач на проценты. Задача В6 уровня 3 нацелена на развитие инициативы учащихся дополнять рисунок к задаче недостающими условиями и расчетами. Тест уровня 3
Тексты всех задач тестов уровня 3 уже имеют лишь подчеркивание основного вопроса текстовой задачи. Прохождение этих тестов рассчитано на закрепление и отработку способов решения элементарных задач, на закрепление появляющихся у учащихся от уровня к уровню успехов, как в развитии метапредметных, так и - предметных умений. Каждая карточка-вариант 4-го уровня уже содержит по 6 задач за счет введения двух типов задачи В3: элементарного алгебраического и элементарного логарифмического. Задача В2 представляет собой смесь диаграмм и графиков дискретных и непрерывных процессов. Задача В4 усложнена нахождением площади невыпуклого многоугольника, но на все той же клетчатой бумаге. Только на четвертом уровне вводятся задачи на проценты, в качестве расчета скидки и наценки, но при этом задачи В1 и В5 подобраны с удобными для счета числовыми значениями. Предполагается, что решение задач на проценты этого уровня должно осуществляться привычным для каждого учащегося способом. Сравнительный анализ эффективности различных способов нахождения процентов целесообразно провести при решении тестов пятого уровня, где их число в каждом тесте увеличено и усложнено неудобными для счета числовыми данными. Тест уровня 4
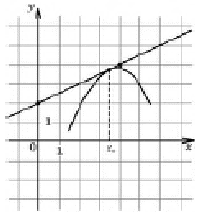
В уровне 4 ключевые слова в текстах задач уже не выделяются. Тесты пятого уровня состоят из 6 задач, среди которых, помимо пяти привычных добавлена задача В8 (на геометрический смысл производной). Поскольку эта задача имеет наглядную опору и несложный геометрический контекст, то формальное усвоение слабоуспевающими учащимися задачи на отыскание тангенса угла наклона касательной к графику функции представляется возможным, в качестве задачи «прозапас», на случай досадной ошибки, описки в любой другой из списка, так называемой «подушки безопасности». Тест уровня 5.
В уровне 5 все задачи В1 и В5 на вычисление процентов. В связи с этим для облегчения решения остальных задач составителями специально упрощена до уровня 1 задача В2. В задаче В4 пятого уровня возможно правдоподобное изображение фигуры на клетчатой бумаге по имеющимся в тексте данным, что позволяет свести задачу к уже знакомой (а это универсальное действие к последнему уровню сложности должно перерастать в умение). При решении тестов предполагалается поэтапно развить универсальные учебные действия, отсутствие которых делает учащегося слабоуспевающим по всем предметам. В большинстве случаев предметные компетенции не могут быть успешно сформированы из-за отсутствия универсальных учебных умений. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
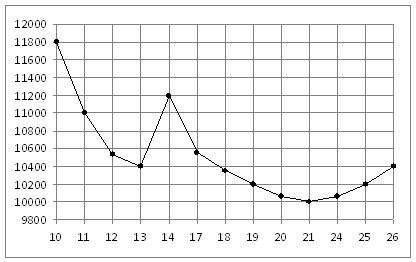. На рисунке жирными точками показана цена никеля на момент закрытия биржевых торгов во все рабочие дни с 10 по 26 ноября 2008 года. По горизонтали указываются числа месяца, по вертикали — цена тонны никеля в долларах США. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку наименьшую цену никеля на момент закрытия торгов в указанный период (в долларах США за тонну).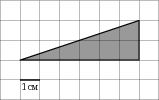
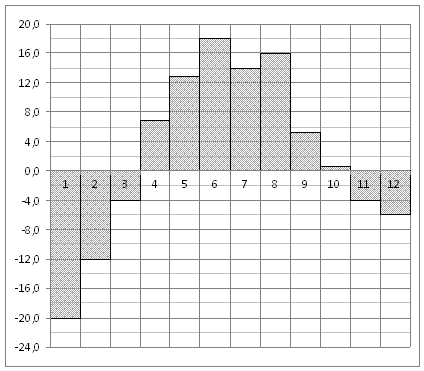1 см. Ответ дайте в квадратных сантиметрах.
. На диаграмме показана среднемесячная температура воздуха в Екатеринбурге (Свердловске) за каждый месяц 1973 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Определите по диаграмме наименьшую среднемесячную температуру в период с мая по декабрь 1973 года включительно. Ответ дайте в градусах Цельсия.
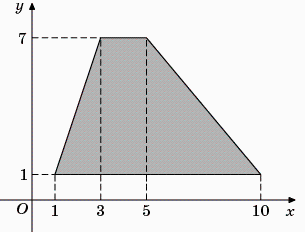. Найдите площадь трапеции, вершины которой имеют координаты (1;1), (10;1), (5;7), 3;7). 
. В таблице приведены цены на стекло и на резку стекол. Сколько рублей будет стоить самый дешевый заказ?
. 
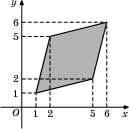. Найдите площадь ромба, изображенного на рисунке.
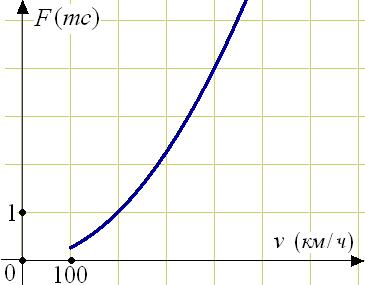. Когда 
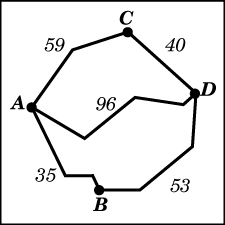. Из пункта A в пункт D ведут три дороги. Через пункт B едет грузовик со средней скоростью 
км/ч, через пункт C едет автобус со средней скоростью 
км/ч. Третья дорога — без промежуточных пунктов, и по ней движется легковой автомобиль со средней скоростью 
км/ч. На рисунке показана схема дорог и расстояние между пунктами по дорогам. 
..
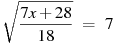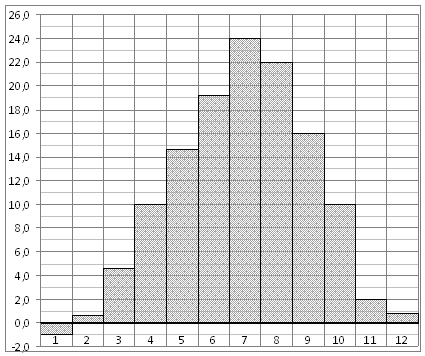. На диаграмме показана среднемесячная температура воздуха в Симферополе за каждый месяц 1988 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. 
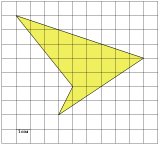. Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см 
руб., он получает сертификат на 1000 рублей, который можно обменять в том же магазине на любой товар ценой не выше 1000 рублей. Если покупатель участвует в акции, он теряет право возвратить товар в магазин. Покупатель И. хочет приобрести пиджак ценой 9500 р., рубашку ценой 800 р. и галстук ценой 500 р. В каком случае И. заплатит за покупку меньше всего:
.
. Если уравнение имеет более одного корня, в ответе запишите больший из корней.
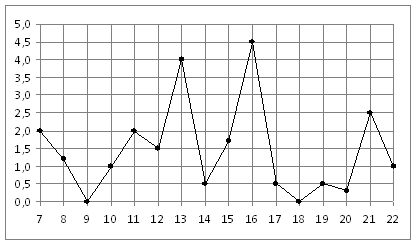. На рисунке жирными точками показано суточное количество осадков, выпадавших в Мурманске с 7 по 22 ноября 1995 года. По горизонтали указываются числа месяца, по вертикали — количество осадков, выпавших в соответствующий день, в миллиметрах. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, какое наибольшее количество осадков выпадало в указанный период. Ответ дайте в миллиметрах.
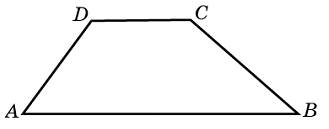. Основания трапеции равны 1 и 3, высота — 1. Найдите площадь трапеции.
и касательная к нему в точке с абсциссой 
. Найдите значение производной функции 
в точке 