«Свойства логарифмов»
 Скачать 34.25 Kb. Скачать 34.25 Kb.
|
| Тема урока: «Свойства логарифмов» Цели и задачи: рассмотреть и доказать свойства логарифмов, начать работу по выработке навыков их применения. Организационный момент (1мин) О целях и задачах урока Устная работа ( слайд№2) (5мин) ▪ Дать определение: logax log34 log56 log√32 log115/9 log0,27 ▪ Вычислить: (предлагаю проговорить определение) log28 log93 log41 log51/25 log31/√3 log0,20,008 Ответ: 3 1/2 0 -2 -1/2 3 ▪ Чему равно: a logax ? (повторяем основное логарифмическое тождество; слайд№3) ▪ Вычислить: 2 log25 9 log34 5 log253 6 log1/65 √7 log736 Ответ: 5 16 √3 1/5 6 Диктант (слайд№4)(5мин) ▪Вычислить 1вариант 2вариант log√77 log5√5 log1/327 log41/16 log61/36 log1/232 lg0,01 log28√2 log39√3 lg1000 4log47 11 log115 36 log63 2 log827 (собираю работы на проверку) Объяснение нового материала (12мин) Задаю вопрос: «Чему равен log1/3264√2?» Проговаривая определение логарифма, учащиеся затрудняются ответить на поставленный вопрос. Возникла проблема, как вычислить этот логарифм. Решить эту проблему помогут свойства логарифмов. Записываем тему урока в тетрадь. Предлагаю обратить внимание на основание и число, стоящее под знаком логарифма, в данном примере. Числа 1/32 и 64√2 являются степенью числа 2. Далее предлагаю вычислить log264√2. Получаем запись: log226,5=6,5 (по определению логарифма) Так как эта запись верна, то верно: log226,5=6,5•1=6,5•log22 Прошу учащихся сравнить левую часть и правую часть равенства и сделать вывод. Получаем: logaxp=p•logax Далее предлагаю вычислить log1/322.Получаем запись: log2-5 2=-1/5 (по определению логарифма) Так как эта запись верна, то верно: log2-52=-1/5•1=-1/5•log22 Прошу сравнить левую и правую часть равенства и сделать вывод. Получаем: logap x=p• logax Кроме этих свойств у логарифма есть еще и другие. Предлагаю доказать теорему. Теорема. Пусть a>0, a≠1, x>0, y>0, p- любое действительное число. Тогда справедливы формулы: loga(xy) = logax + logay logax/y = logax - logay logaxp = p• logax log apx = 1/p• logax , p≠0 (формулы на слайде№5) Доказательство: Докажем первое свойство, а остальные предлагаю доказать дома аналогично. alogax+logay = alogax • alogay = x • y Ч.Т.Д. Теперь мы сможем вычислить предложенный логарифм.(объясняю) Log1/3264√2=log2-526,5=6,5•(-1/5)=-1,3 Посмотрим, как применяются все свойства логарифмов для вычислений. ▪ log618 + log62 = log6(18•2) = log636 = 2 ▪ log12 48 - log124 = log1248/4 = log1212 = 1 ▪ log3243 = log335 = 5•log33 = 5 • log1/813 = log3-4 3 = -1/4•log33 = -1/4 Упражнения (слайд№6)(10мин) Вычислить:
Учащиеся решают самостоятельно, но после проверки ответа в каждом примере решение показываю на слайде. Повторение (слайд№7)(10мин) Повторим вопрос существования логарифма. logax a>0 a≠1 x>0 П  ри каких значениях x существует логарифм: Ответы: ри каких значениях x существует логарифм: Ответы:
Эта часть примеров решается устно, остальные письменно.
Решение: (25-x2)(2x+1)>0 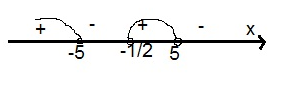 Ответ: (-∞; -5) и (-1/2; 5). Ответ: (-∞; -5) и (-1/2; 5).
Решение: (3x-x2)(x2-x-6)>0 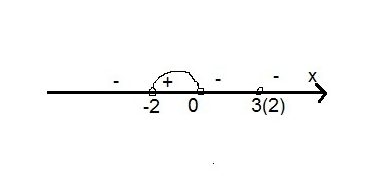 Ответ: (-2; 0). Домашнее задание и поведение итогов (2мин) |