Неполные квадратные уравнения
 Скачать 55.13 Kb.
|
| Урок по алгебре в 8 классе. Тема " Неполные квадратные уравнения". Учителя: Крамаренко Т.Н., Зенина Н.Г. Тип урока: урок изучения нового материала Цели урока: Образовательные: ввести понятия квадратного уравнения, приведённого, неполного квадратного уравнения; расширение и углубление знаний учащихся о решении уравнений; организация поисковой деятельности при решении неполных квадратных уравнений; совершенствование вычислительных навыков. Развивающие: развитие умения приобретать новые знания; использование для достижения поставленной цели уже полученные знания; формирование умений применять приемы: наблюдения, сравнения, систематизации и обобщения, переноса знаний в новую ситуацию; расширять математический и общий кругозор, развивать устную математическую речь и навыки нестандартного мышления. Воспитательные: воспитание навыков самоконтроля и взаимоконтроля; выработка желания и потребности обобщать полученные факты и знания; развитие самостоятельности и творчества. Оборудование: компьютер, экран, проектор. Ход урока.
Сегодня мы начинаем изучать важную не только в курсе 8 класса, но и для всей школьной математики, главу «Квадратные уравнения», а значит, научимся решать новый для нас вид уравнений (слайд 1,2). А теперь давайте вместе искать ответы на эти вопросы. 2. Этап актуализации знаний. В 7 и 8 классе мы уже рассматривали (и даже решали) квадратные уравнения: х² ‒ 4 = 0, 3х² + 2х = 0; х² ‒ 6х + 9 = 0 (слайд3). На какие вопросы вы хотели бы уже сегодня получить ответы? (Слайд 4)
3. Изучение нового материала. Слайд 5.    Что общего в этих уравнениях? В чем различие? (Члены, содержащие квадрат неизвестной.) (Все они имеют одинаковое строение:   и х умножают на некоторые числа, а потом прибавляют слагаемое, не содержащее х ).Такие уравнения называют квадратными. Давайте познакомимся с определением квадратного уравнения п.21, с.111. Почему же это уравнение получило название квадратного? (Слайд 6) (Степень многочлена, стоящего в левой части, равна 2, а вторую степень называют квадратом) Чем вызвано ограничение  ?(если а=0, то  , и уравнение перестанет быть квадратным)Запишите это определение себе в тетради. а, в и с – некоторые числа - говорится в определении, причем а и в стоят перед и х, а с не содержит х. Как бы вы их назвали? (первый коэффициент, второй коэффициент, свободный член). Записываем: а - первый коэффициент (число, стоящее перед );в – второй коэффициент (число, стоящее перед х); с – свободный член (не содержит х). Слайд 7. а = 1 - приведенное квадратное уравнение: х2 + bх + с = 0 а ≠ 1 – неприведенное квадратное уравнение Решим №513 – устно (по одному примеру по очереди). Слайд 8. Слайд 9. Интересно, а что будет, если эти коэффициенты по очереди или все сразу (кроме а) превратятся в нули. Давайте проведем исследование. Слайд 10, 11. Сформулируйте определение квадратного уравнения в котором отсутствует коэффициент или свободный член. Квадратное уравнение  , называют неполным квадратным, если хотя бы один из его коэффициентов b или c равен 0.Назовите виды неполных квадратных уравнений.    К доске приглашаются три учащихся одновременно. Задание №1. Рассмотреть случай, когда в=0 и с=0 Задание №2. Рассмотреть случай, 0когда в=0. Задание №3. Рассмотреть случай, когда с=0. (учащиеся на месте работают самостоятельно - по рядам) I ученик (слайд12). Если в=0 и с=0, то - неполное квадратное уравнение.Это равенство верно только при  - всегда один корень.II ученик(слайд 13). Если в=0, то  - неполное квадратное уравнение (Такие уравнения мы уже решали в предыдущей главе «Квадратные корни». Напомни нам, как решают уравнения вида 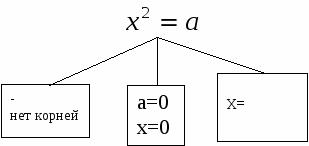 ) Сделай вывод. Вывод. Неполное квадратное уравнение вида ах2 + с = 0; 1) Если  > 0, то уравнение имеет два корня.х1=  , х2= .2) Если < 0, то корней нет.II ученик(Слайд14). Если с=0, то  - неполное квадратное уравнение (С такими уравнениями мы тоже уже встречались в 7 классе, когда учились выносить общий множитель за скобки) Напомни нам, в каком случае произведение множителей равно нулю. ах2 + bх = 0; х = 0, х = –  ; два корня.Сделай вывод. Вывод. Неполное квадратное уравнение вида всегда имеет два корня, один из которых равен нулю, а другой равен  .III ученик Если в=0 и с=0, то - неполное квадратное уравнение.Это равенство верно только при - всегда один корень.Учащимся предлагается составить систематизирующую схему. Работа выполняется совместными усилиями учащихся на доске, а потом опорный конспект переносится в тетради. 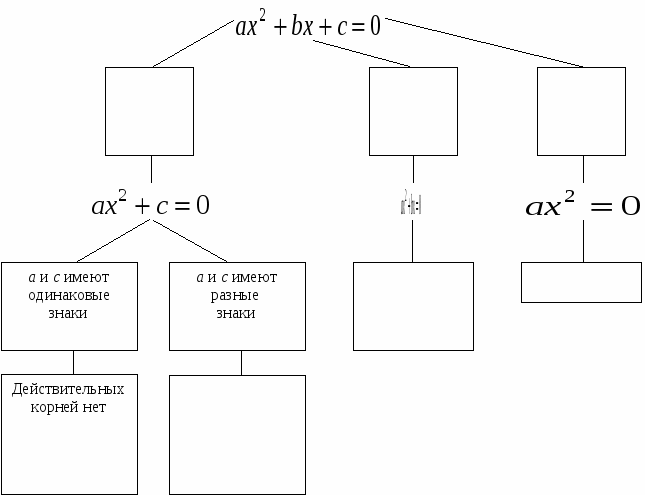 4. Проверка первичного понимания изученного 1. Из предложенных уравнений выберите неполные квадратные. Выпишите их в тетрадь. Слайд 15. 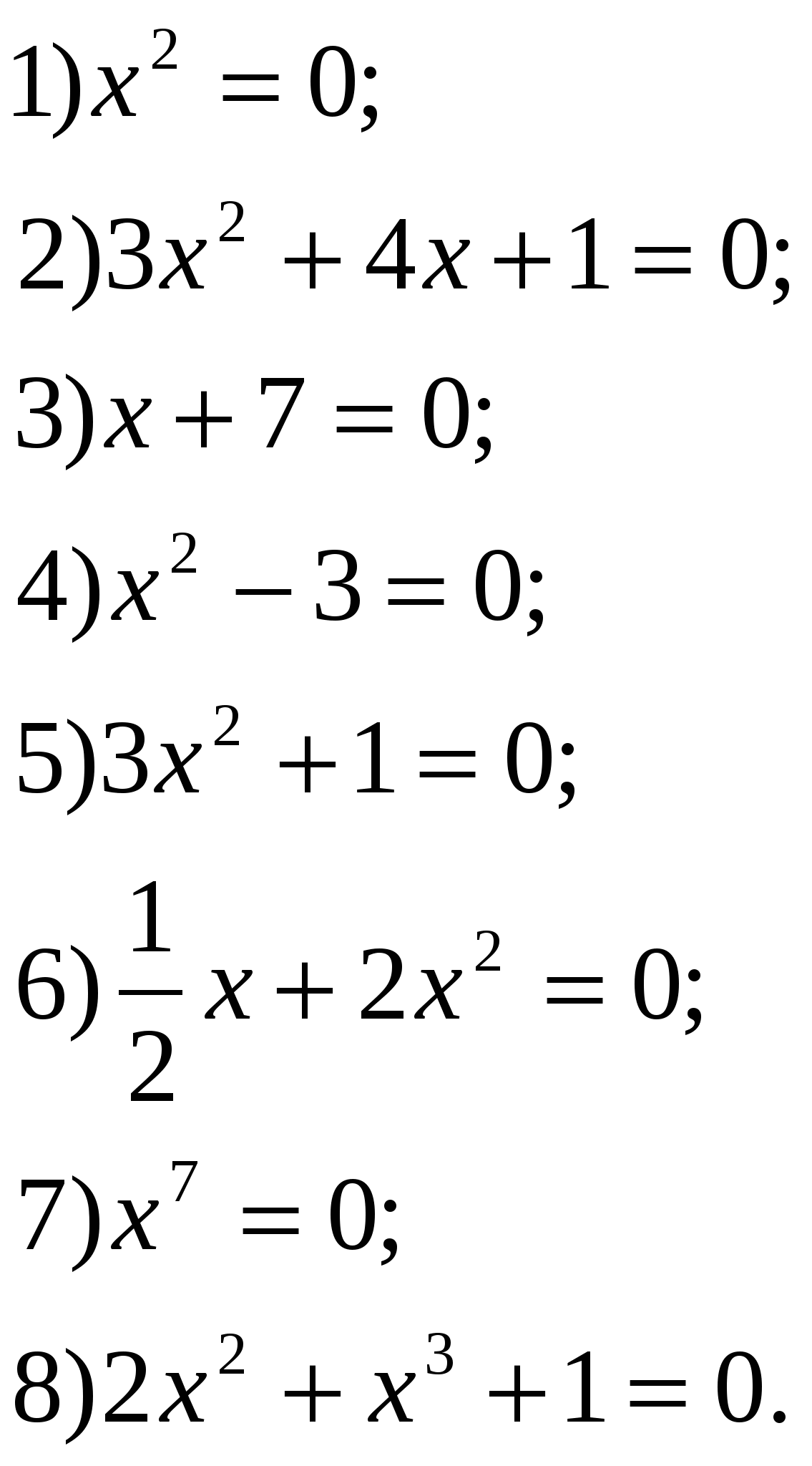 В тетрадях появляется запись: 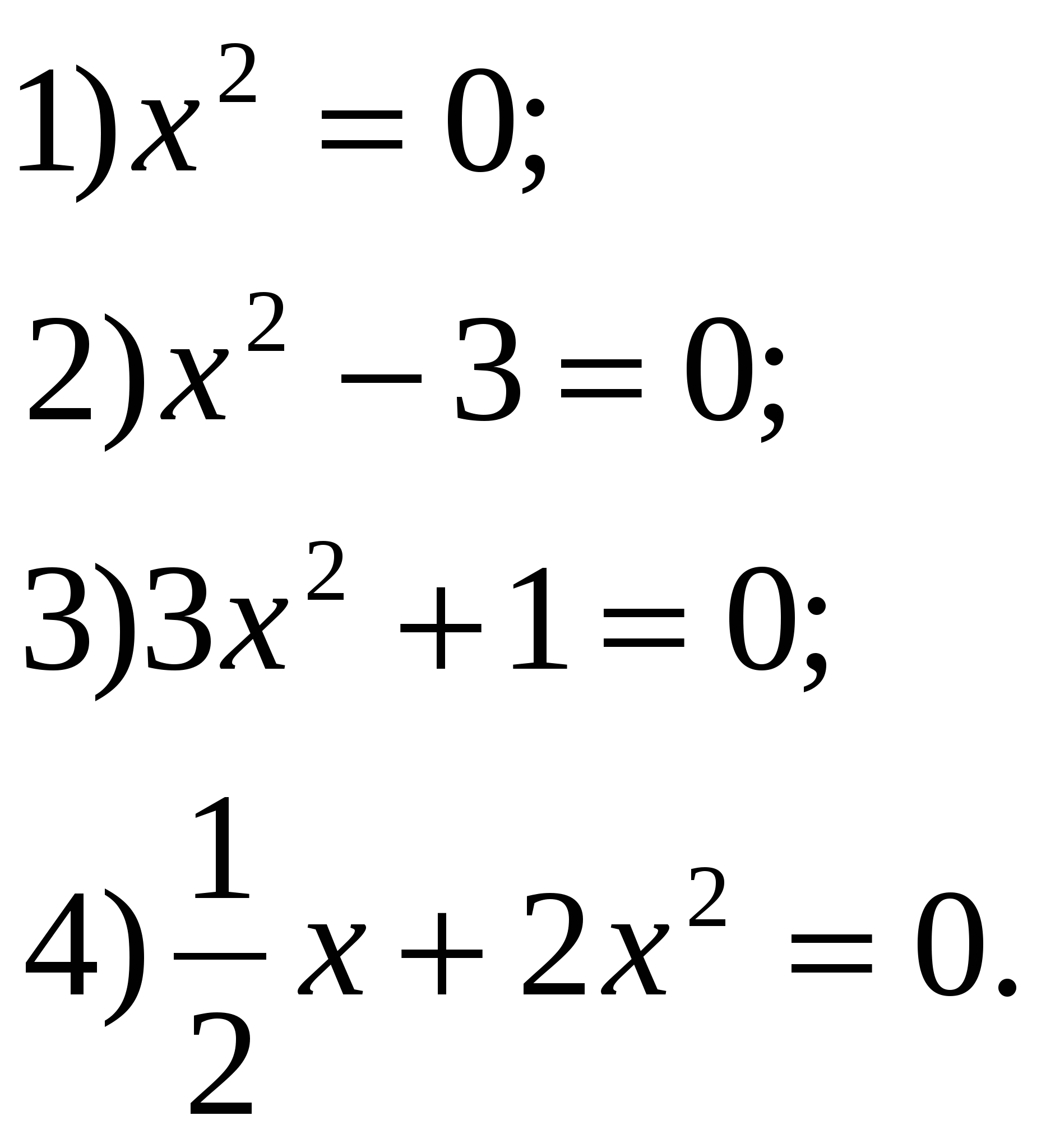 Сколько корней может иметь неполное квадратное уравнение? Решите выписанные неполные квадратные уравнения. 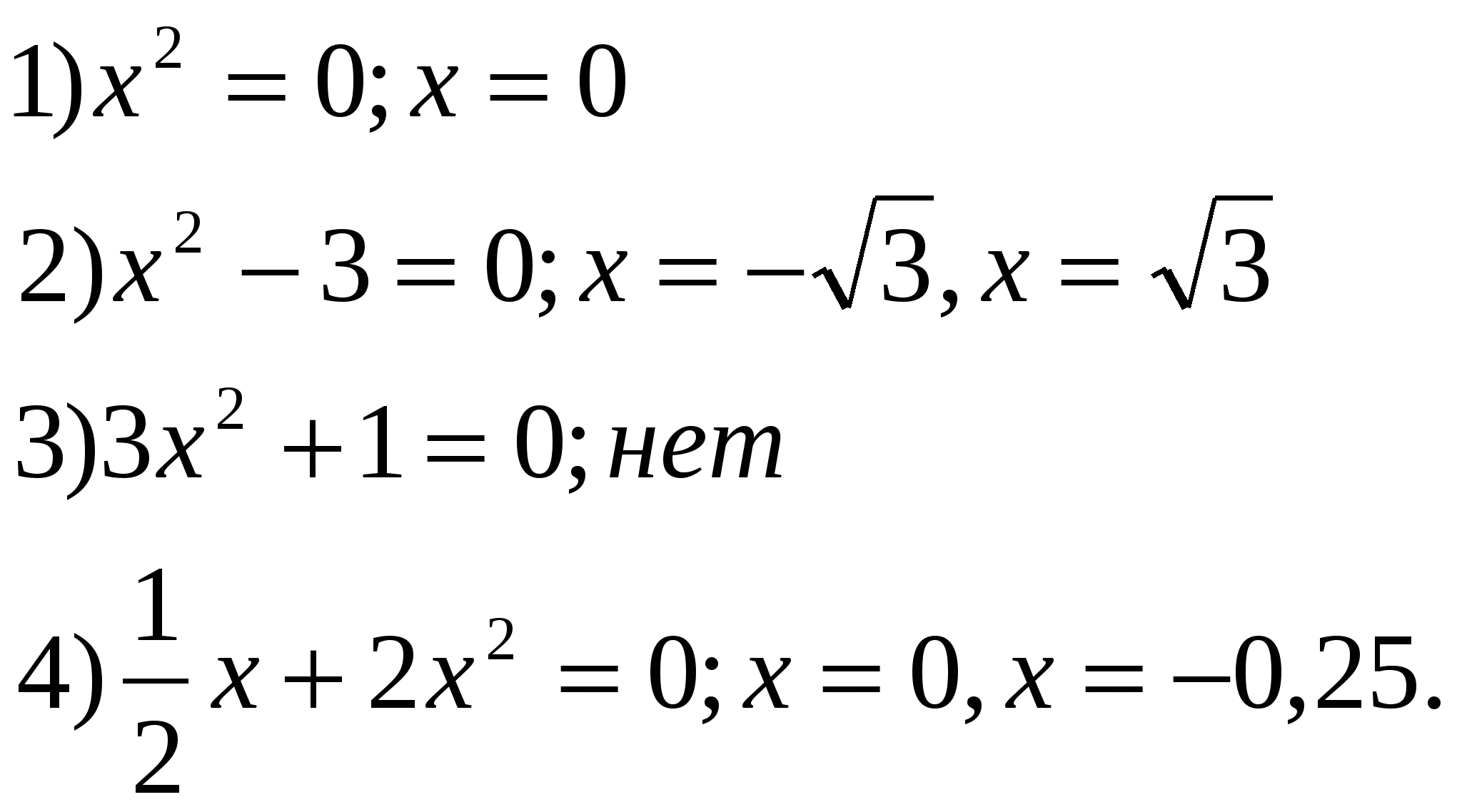 2. Запишите квадратные уравнения с указанными коэффициентами. Слайд 16. 1) a=1, b=0, c=16; 2) a=-1, b=5, c=0; 3) b=0, a=-3, c=0; 4) c=-8, a=1, b=0; 5) a=1,5, c=0, b=-3; 6) b=  a= c=0.В тетради появляется запись: 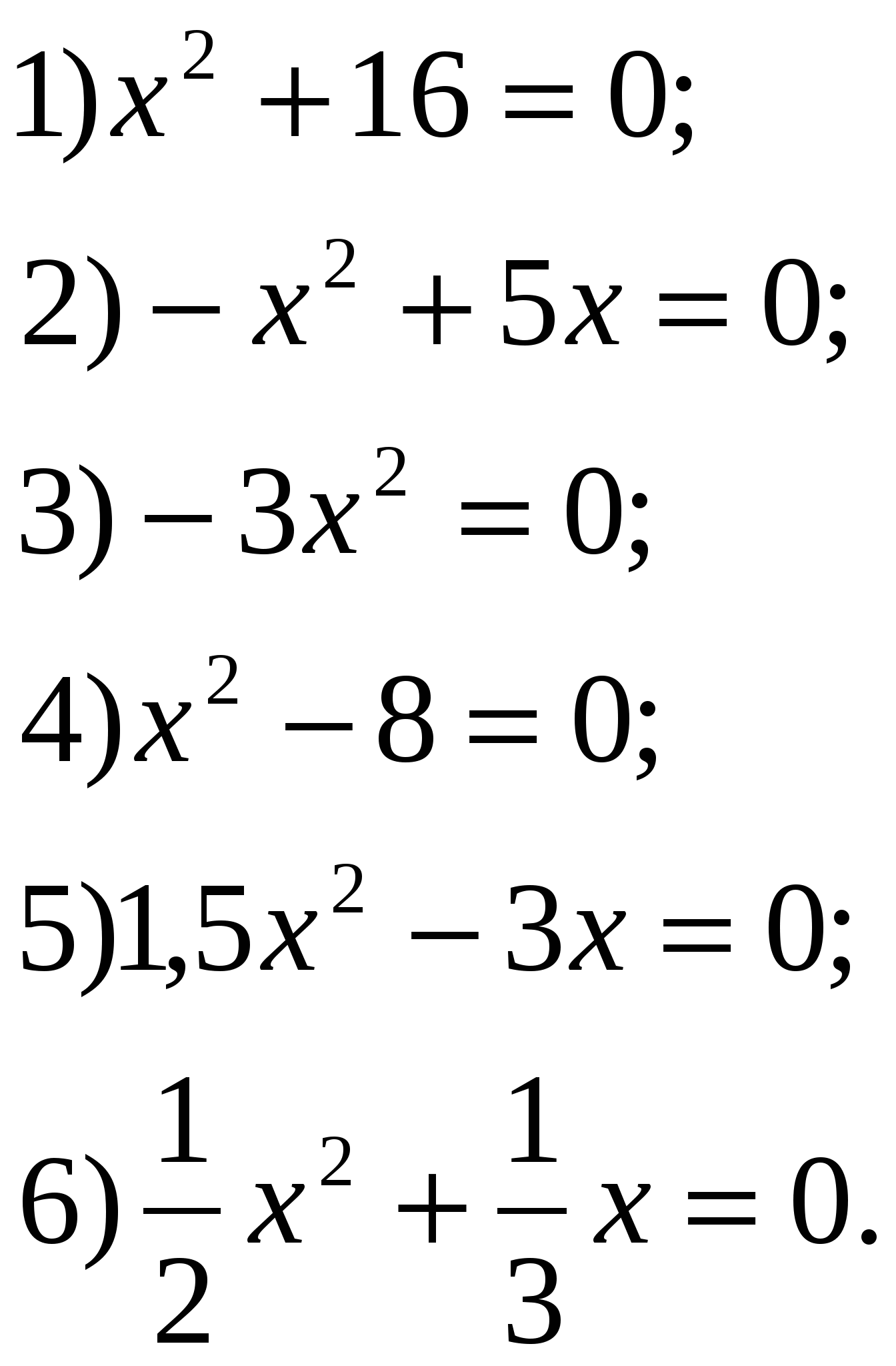 Установите соответствие между уравнениями и следующими утверждениями: а) уравнение имеет два корня; б) уравнение имеет один корень; в) уравнение не имеет корней. Рядом с условием записывается буква соответствующего утверждения. 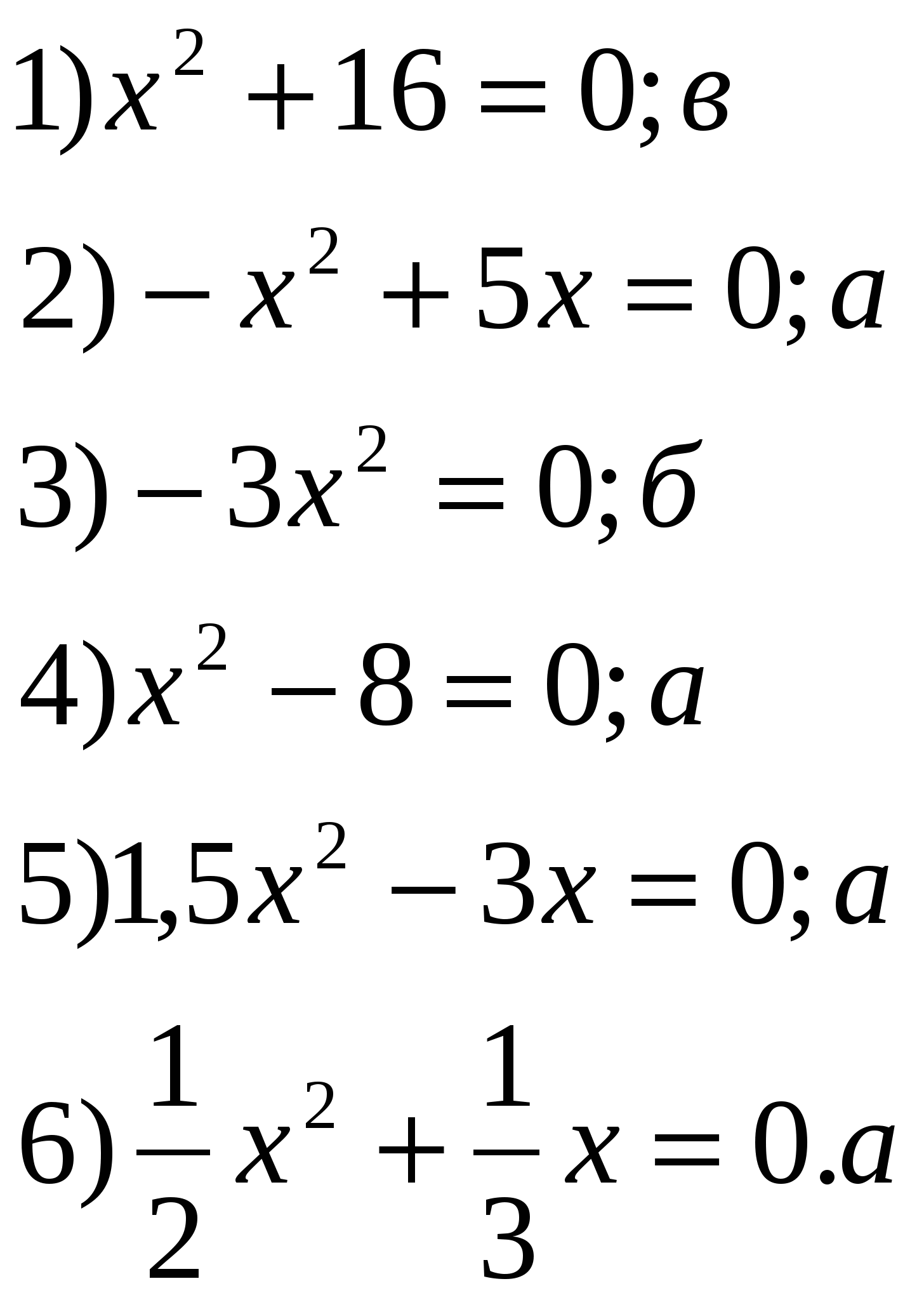 А теперь решим уравнения: №515 (а,в,г), №517 (б,г,д). Проверили! Слайд 17, 18. А теперь решим уравнение с параметром. При каких значениях а данное уравнение является неполным квадратным уравнением.  Слайд 19,20.5. Подведение итогов урока Какое же уравнение называется квадратным? Почему ? Как называются числа а, в и с?Сколько видов неполных квадратных уравнений мы узнали? Назовите их общий вид. Как решают уравнения I вида? II вида? III вида? Рефлексия (слайд 22). Урок заканчивается. Ребята! Получили вы ответы на интересующие вас вопросы? Поняли вы, что нас впереди ждут интересные, захватывающие, а самое главное – важные темы? 6. Информация о домашнем задании: (слайд 23) П. 21 (определения), №518, 521 (а,в), 523 а. Дополнительно (для учащихся с повышенным интересом) №520, №532. |