Урок по теме: «Решение квадратных уравнений различными способами». 8 класс Автор: Шакалова И. В
 Скачать 63.74 Kb. Скачать 63.74 Kb.
|
| Муниципальное бюджетное общеобразовательное учреждение основная общеобразовательная школа №21 х. Свободы муниципального образования Курганинский район Урок по теме: « Решение квадратных уравнений различными способами». 8 класс Автор: Шакалова И.В. Учитель математики. 2013 год. Цели урока:
Оборудование: компьютер, проектор, листы с заданиями, тесты. Ход урока:
нет корней; два корня; один корень. (Корней не будет, когда х² < 0. Два корня будет при решении обычного квадратного уравнения. Уравнение будет иметь один корень, если х² = 0.) Варианты уравнений: 6х² + 3 = 0; -х² = 0; х² - 4х +4 = 0; 4х² - 16 = 0; 5х² + 15 = 15.
4х² - 20х + 25 = 0, учитывая, что есть три способа его решения. Первый способ. Вычислить корни квадратного уравнения можно через дискриминант. Потом находятся корни квадратного уравнения. D = b² - 4ac = 0, х = 2,5. Второй способ. Второй коэффициент квадратного уравнения четное число, поэтому можно вычислить его корень через k. D = k² - ac = 0, х = 2,5. Третий способ. Разложить квадратное уравнение на множители. Уравнение преобразуется так, чтобы в левой его части получился квадрат двучлена. 4х² - 20х + 25 = (2х – 5)², х = 2,5.
а) 2х² + 8х – 6 = 0. Ответ: х² + 4х – 3 = 0. б) 6х² – 18х - 60 = 0. Ответ:3х² - 9х – 30 = 0.
1) Один из корней квадратного уравнения х² + pх – 33 = 0 равен -3. Найдите другой корень и коэффициент p. Решение: используя теорему Виета, получаем х1 ∙ х2 = 33, х2 = -11, p = - (-3 -11) = 14. 2)Определите, сколько корней имеет квадратное уравнение, не решая его. а) 7х² + х +1 = 0, D = -27, D < 0. Ответ: корней нет. б) 2х² + 3х +1 = 0, D = 9 - 4∙2 = 1, D > 0. Ответ: два корня. в) 25х² +10х + 1= 0, D = 100 – 4∙ 25 = 0, D = 0. Ответ: один корень. г) 2х² – 50 = 0. Решение: 2х² – 50 = 0; х² - 25 = 0; х² = 25. Так как 25 > 0, то уравнение имеет два корня. Ответ: два корня. 3)При каком значении параметра p уравнение 3х² + pх - p = 0 имеет один корень? Решение. 3х² + pх - p = 0 Квадратное уравнение имеет один корень, если D = 0. D = p² - 4∙3∙ (- p) = p² + 12 p, p² + 12 p = 0, p1 = 0, p2 = -12. Ответ: 0; -12. 4)Решите квадратное уравнение, учитывая, что второй коэффициент является четным числом. х² – 10х – 39 = 0, в = -10, к = -5, с = -39, D1 = k² - ac, х1 = 13, х2 = -3. Ответ:13, -3. 5) Задача. Одна сторона прямоугольника на 5 см больше другой, а его площадь равна 84 см². Найдите стороны прямоугольника. Решение. 1 этап. Пусть х см – ширина прямоугольника, (х+5) см – длина прямоугольника. Тогда х ∙ (х + 5) см² - его площадь или 84 см². Уравнение: х ∙ (х + 5) = 84. 2 этап. х∙ (х + 5) – 84 = 0, D = 361, х1 = 7, х2 = -12. 3этап. х2 = -12 < 0 – не удовлетворяет условию задачи. Так что 7 см – ширина прямоугольника, 7 + 5 = 12 (см) – длина прямоугольника. Ответ: 7 см, 12 см. 6)Решите уравнение, используя метод введения новой переменной: 4х 4 – 37 х² + 9 = 0
1 группа. Решите квадратное уравнение: 1) х² + 5х + 6 = 0, 2) 9х² – 20х – 21 = 0, 3) 3х² – 12 = 0, 4) х² + 9 = 0. 2 группа. Решите уравнение, используя метод введения новой переменной: а) (х² – 3х +1) (х² -3х +3) = 3 б) х² - 4 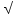 3х + 12 = 0 3х + 12 = 0в) Один из корней уравнения х² + px +24 = 0 равен 8; найдите p. 4. Итоги урока. Учитель еще раз обращает внимание на теоретические факты, которые вспоминали на уроке, говорит о необходимости выучить их. Отмечает успешную работу на уроке отдельных учащихся и выставляет оценки. Оценки за самостоятельную работу учитель объявляет и выставляет на следующем уроке. 5. Домашнее задание. В качестве домашнего задания учащиеся получают тесты. Тест. 1 группа. № 1. Найдите дискриминант квадратного уравнения: x² + 5x – 6 = 0 а) 1; б) 49; в) 37; г) 0. № 2. Определите число корней уравнения x²+ 6x + 9 = 0 а) нет корней; б) 1 корень; в) 2 корня; г) 3 корня. № 3. Решите уравнение: x² – 5x + 6 = 0 а) -1; -6; б) 1; 6; в) 2; 3; г) -2; -3. № 4. Решите уравнение: 2x² + 3x = 0 а) -1,5; б) -1,5; 0; в) нет корней; г) 0; 1,5. № 5. Решите уравнение: 2x² + 32 = 0 а) -4;4; б) 4; в) нет корней; г) 0. № 6 Чему равно произведение корней уравнения x² – 16x + 64 = 0? а) 64; б) – 64; в) 16; г) -16. 2группа. Решите уравнение: а) 4а² + 5 = а б) 4х 4 + 7х² – 8 = 0 в) (х² + 4х)( х² + 4х – 17) + 60 =0 Разложите на множители: 2х² – 5х + 2 = 0 При каком значении параметра а уравнение имеет два корня? ах²+ 5х – 2 = 0. |