Список литературы
 Скачать 216.65 Kb. Скачать 216.65 Kb.
|
                               СОДЕРЖАНИЕ СОДЕРЖАНИЕВВЕДЕНИЕ 1. ХАРАКТЕРИСТИКА ТЕКСТОВОЙ ЗАДАЧИ 2. ОБУЧЕНИЕ ШКОЛЬНИКОВ ПРИЕМАМ РЕШЕНИЯ ТЕКСТОВЫХ ЗАДАЧ 2.1 Задачи на движение 2.2. Задачи на совместную работу 2.3 Задачи на концентрацию смесей и сплавов 2.4 Задачи на проценты ЗАКЛЮЧЕНИЕ СПИСОК ЛИТЕРАТУРЫ ПРИЛОЖЕНИЯ ВВЕДЕНИЕ Текстовые задачи всегда присутствовали в математическом образовании в России. Никто не подвергал сомнению их важность в обучении, и никто не считал их особенно сложными. Задачи являются материалом для ознакомления учащихся с новыми понятиями, для развития логического мышления, формирования межпредметных связей. Задачи позволяют применять знания, полученные при изучении математики, при решении вопросов, которые возникают в жизни человека. Этапы решения задач являются формами развития мыслительной деятельности. Уже в начальной школе дети решают некоторые простые задачи. С годами задачи становятся все сложнее. В результате выпускники многих средних школ имеют достаточный опыт в решении задач. Но статистические данные анализа результатов проведения ЕГЭ с момента его существования говорят о том, что решаемость задания, содержащего текстовую задачу, составляет год от года чуть больше или меньше 30%. Такая ситуация позволяет сделать вывод, что большинство учащихся не в полной мере владеет техникой решения текстовых задач и не умеет за их часто нетрадиционной формулировкой увидеть типовые задания, которые были достаточно хорошо отработаны на уроках в рамках школьной программы. Полный минимум знаний, необходимый для решения всех типов текстовых задач, формируется в течение первых девяти лет обучения учащихся в школе. В обучении математике велика роль текстовых задач. Решая задачи, учащиеся приобретают новые математические знания, готовятся к практической деятельности. Задачи способствуют развитию их логического мышления. Большое значение имеет решение задач и в воспитании личности учащихся. Поэтому важно, чтобы учитель имел глубокие представления о текстовой задаче, о её структуре, умел решать такие задачи различными способами. Текстовая задача – есть описание некоторой ситуации на естественном языке с требованием дать количественную характеристику какого-либо компонента этой ситуации, установить наличие или отсутствие некоторого отношения между её компонентами или определить вид этого отношения. Решение задач – это работа несколько необычная, а именно умственная работа. А чтобы научиться какой-либо работе, нужно предварительно хорошо изучить тот материал, над которым придётся работать, те инструменты, с помощью которых выполняется эта работа. Значит, для того чтобы научиться решать задачи, надо разобраться в том, что собой они представляют, как они устроены, из каких составных частей они состоят, каковы инструменты, с помощью которых производится решение задач. Каждая задача – это единство условия и цели. Если нет одного из этих компонентов, то нет и задачи. Это очень важно иметь в виду, чтобы проводить анализ текста задачи с соблюдением такого единства. Это означает, что анализ условия задачи необходимо соотносить с вопросом задачи и, наоборот, вопрос задачи анализировать направленно с условием. Их нельзя разрывать, так как они составляют одно целое. Математическая задача – это связанный лаконический рассказ, в котором введены значения некоторых величин и предлагается отыскать другие неизвестные значения величин, зависимые от данных и связанные с ними определенными соотношениями, указанными в условии. Любая текстовая задача состоит из двух частей: условия и требования (вопроса). В условии соблюдаются сведения об объектах и некоторых величинах, характеризующих данные объекта, об известных и неизвестных значениях этих величин, об отношениях между ними. Требования задачи – это указание того, что нужно найти. Оно может быть выражено предложением в повелительной или вопросительной форме («Найти площадь треугольника.» или «Чему равна площадь прямоугольника?»). Рассмотрим задачу: На тракторе «Кировец» колхозное поле можно вспахать за 10 дней, а на тракторе «Казахстан» – за 15 дней. На вспашку поставлены оба трактора. За сколько дней будет вспахано это поле? В задаче пять неизвестных значений величин, одно из которых заключено в требовании задачи. Это значение величины называется искомым. Иногда задачи формируются таким образом, что часть условия или всё условие включено в одно предложение с требованием задачи. В реальной жизни довольно часто возникают самые разнообразные задачные ситуации. Сформулированные на их основе задачи могут содержать избыточную информацию, то есть, такую, которая не нужна для выполнения требования задачи. На основе возникающих в жизни задачных ситуаций могут быть сформулированы и задачи, в которых недостаточно информации для выполнения требований. Так в задаче: «Найти длину и ширину участка прямоугольной формы, если известно, что длина больше ширины на 3 метра» – недостаточно данных для ответа на её вопрос. Чтобы выполнить эту задачу, необходимо её дополнить недостающими данными. Одна и та же задача может рассматриваться как задача с достаточным числом данных в зависимости от имеющихся и решающих значений. Рассматривая задачу в узком смысле этого понятия, в ней можно выделить следующие составные элементы: 1. Словесное изложение сюжета, в котором явно или в завуалированной форме указана функциональная зависимость между величинами, числовые значения которых входят в задачу. 2. Числовые значения величин или числовые данные, о которых говорится в тексте задачи. 3. Задание, обычно сформулированное в виде вопроса, в котором предлагается узнать неизвестные значения одной или нескольких величин. Эти значения называют искомыми. Понимая роль задачи и её место в обучении и воспитании ученика, учитель должен подходить к подбору задачи и выбору способов решения обоснованно и чётко знать, что должна дать ученику работа при решении данной им задачи. И все-таки, почему же этот материал труден для учащихся? Разрозненные указания учителей по решению задач быстро забываются учениками, они не приобретают навыков решения текстовых задач. Без конкретной программы деятельности учащихся, без алгоритмов, системы приемов поиска решения задачи трудно организовать процесс решения задач. Поэтому необходимы «ускорители» для приобретения навыков решения : иллюстрация, схемы, таблицы, дополнительные символы, условные знаки, стрелки, способствующие более конкретному наглядному представлению об отношениях между частями задачи, связях между величинами, порядке этих связей. Это позволяет стимулировать у учащихся развитие наглядно-действенного мышления и на основе его в дальнейшем – образного мышления. Поиск решения текстовой задачи путем составления таблицы дает возможность охватить взором отношения между элементами всей задачи. Можно выделить основные причины, вызывающие у учащихся затруднения при поиске решения: 1. Неумение выделить величины, о которых идет речь в задаче. 2. Неумение установить функциональную зависимость в математических символах. 3. Неумение выразить эту зависимость в математических символах. 4. Слабые навыки схематической и символической записи условия, способствующей анализу задачи, выражению зависимостей между величинами, входящими в задачу.
Начинают решение задачи обычно с тех неизвестных величин, для которых потом будут составлять уравнения. Необязательно брать в качестве таких неизвестных те величины, которые требуется определить в задаче. Иногда удобнее найти другие величины: те, для которых сравнительно легко составляются уравнения (или уравнения имеют простой вид) и через которые несложно выражаются искомые величины. Если составленных уравнений получается меньше, чем неизвестных, то следует внимательно посмотреть, все ли условия задачи учтены при составлении уравнений или не введены ли лишние неизвестные. Часто неизвестные данной задачи имеют естественные ограничения: например, если х – масса какого-либо вещества, то х – неотрицательное число; если х – количество человек, то х – целое неотрицательное число; если х – цифра числа, то х может принимать лишь следующие значения: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9; и т.д. Текстовые задачи условно можно разделить на типы: задачи на движение, совместную работу, проценты, концентрация и смеси, числовые зависимости и т.д. Рассмотрим некоторые из них. 2.1 Задачи на движение Основными величинами задач на движение являются: пройденный путь s, скорость v, время t. Зависимость между ними при равномерном движении выражается формулой 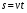 Все величины должны быть в одной системе единиц. 1) Движение тела по реке. Если тело с собственной скоростью vсобств. движется по реке, скорость течения которой равна vтеч., то скорость движения по течению vпо теч. = vсобств. + vтеч. скорость движения против течения vпр теч. = vсобств. - vтеч скорость течения vтеч. = (vпо теч. - vпр теч.) собственная скорость vсобств. = (vпо теч. + vпр теч.) Пример. Пароход, отчалив от пристани А, спустился вниз по течению реки на 60 км до устья впадающего в реку притока и поднялся вверх по притоку (против течения) на 20 км до пристани В. Весь путь от А до В пароход прошел за 7 ч. Скорость течения реки и скорость течения притока равна 1 км/ч. Найти собственную скорость парохода. Решение Пусть х км/ч – собственная скорость парохода. Тогда по течению пароход шел со скоростью (х+1) км/ч, а по притоку – со скоростью (х-1) км/ч. На путь по реке пароход затратил 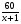 ч, а на путь по притоку - ч, а на путь по притоку - 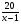 ч. Весь путь он прошел за 7 часов. Составим и решим уравнение ч. Весь путь он прошел за 7 часов. Составим и решим уравнение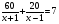 . .Корни этого уравнения х1=11 х2=3/7 Скорость парохода не может быть меньше 1 км/ч, так как он двигался по притоку против течения, скорость которого 1 км/ч. Следовательно, собственная скорость парохода 11 км/ч Ответ: 11 км/ч 2) Задачи на совместное движение. Начиная с 5-го класса, ученики часто встречаются с этими задачами. Еще в начальной школе учащимся дается понятие «общей скорости». В результате у них формируются не совсем правильные представления о скорости сближения и скорости удаления (данной терминологии в начальной школе нет). Чаще всего, решая задачу, учащиеся находят сумму. Начинать решать эти задачи лучше всего с введения понятий: «скорость сближения», «скорость удаления». Для наглядности можно использовать движение рук, объясняя, что тела могут двигаться в одном направлении и в разном. В обоих случаях может быть и скорость сближения и скорость удаления, но в разных случаях они находятся по-разному. Решать задачи такого типа можно с учащимися двумя способами:
При движении тел навстречу друг другу время, через которое они встретятся, равно 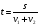 , где , гдеs – расстояние между телами; v1 и v2 – скорости тел. При движении тел в одну сторону (v1 > v2), время, через которое первое тело догонит другое, равно 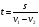 . .
При разборе задачи даются следующие вопросы. 1. С помощью движения рук выясняем, как двигаются тела относительно друг друга (в одном направлении, в разных). 2. Выясняем, каким действием находится скорость (сложением, вычитанием) 3. Определяем, какая это скорость (сближения, удаления). Записываем решение задачи. Пример №1. Из городов А и В, расстояние между которыми 600 км, одновременно, навстречу друг другу вышли грузовая и легковая машины. Скорость легковой 100 км/ч, а грузовой – 50 км/ч. Через сколько часов они встретятся? Учащиеся движением рук показывают, как движутся машины и делают следующие выводы: а. машины движутся в разных направлениях; б. скорость будет находиться сложением; в. так как они движутся на встречу друг другу, то это скорость сближения. Решение: 1. 100+50=150 (км/ч) – скорость сближения. 2. 600:150=4 (ч) – время движения до встречи. Ответ: через 4 часа Пример №2. Мужчина и мальчик вышли из совхоза в огород одновременно и идут одной и той же дорогой. Скорость мужчины 5 км/ч, а скорость мальчика 3 км/ч. Какое расстояние будет между ними через 3 часа? С помощью движения рук, выясняем: а. мальчик и мужчина движутся в одном направлении; б. скорость находится разностью; в. Мужчина идет быстрее, т.е., удаляется от мальчика (скорость удаления). Решение: 1. 5 – 3 =2 (км/ч) – скорость удаления. 2. 2*2=4 (км) – расстояние между мужчиной и мальчиком через 2ч. Ответ: 4 км. 3) Движение по окружности. При движении тел по окружности с постоянными скоростями v1 и v2 (v1 > v2) время между их встречами вычисляется по формулам:
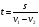 , где s – длина окружности; , где s – длина окружности;
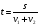 , где s – длина окружности. , где s – длина окружности.Пример. По окружности длиной 60 м равномерно и в одном направлении движутся две точки. Одна из них делает полный оборот на 5 с быстрее другой. При этом совпадение точек происходит каждый раз через минуту. Определите скорости точек. Решение Пусть первая точка проходит полный оборот за х с, а вторая – за у с. Тогда 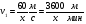 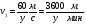 Будем полагать, что x<y, тогда из условия задачи следует уравнение у-х=5 Так как точки встречаются каждую минуту и первая движется быстрее, то она должна за 1 мин пройти полный круг, т.е. 60 м и еще столько, сколько успеет пройти за 1 мин вторая точка, т.е 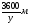 . Отсюда имеем второе уравнение . Отсюда имеем второе уравнение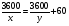 Составим систему и решим ее 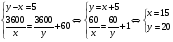 Тогда 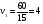 м/с м/с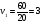 м/с м/сОтвет 4 м/с; 3 м/с 2.2 Задачи на совместную работу Основными величинами задач на совместную работу являются: А - работа, t - время, Р - производительность труда (работа, выполненная в единицу времени). Тогда А = Р ∙ t . При решении этих задач нужно выяснить с учащимися, что возможны два случая: а. объем выполненной работы известен; б. объем выполненной работы неизвестен. 1) Первые задачи удобно решать, используя таблицы. Пример. Два токаря вместе изготовили 350 деталей. Первый токарь делал в день 40 деталей и работал 5 дней, второй работал на 2 дня меньше. Сколько деталей в день делал второй токарь? Составим таблицу .
Объяснение. Так как известны производительность и время работы первого токаря, найдем количество деталей, изготовленных первым токарем. 40 ∙ 5 = 200 (дет.) – изготовил первый токарь. Работая с таблицей, делаем вывод, что можно найти, сколько деталей изготовил второй токарь. 350 – 200 = 150 (дет.) – изготовил второй токарь. Обратив внимание на опорные слова «на…меньше», делаем вывод, что можно найти, сколько дней работал второй. 5 – 2 = 3 (дня) – работал второй токарь. Зная количество и время работы второго токаря, находим его производительность: 150 / 3 = 50 (дет.) – изготовлял второй токарь в день. Уже при решении первых задач, нужно приучать детей к правильной терминологии. 2) При решении задач второго типа обычно всю работу, которую необходимо выполнить, принимают за 1. Тогда производительность труда находят по формуле 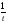 , где t – время, за которое выполняется вся работа, t1 - время выполнения работы первым, t2 - время выполнения работы вторым. , где t – время, за которое выполняется вся работа, t1 - время выполнения работы первым, t2 - время выполнения работы вторым.t = t1 ∙ t2 1 1 1 t1 + t2 t1 t2 t Пример1. Два плотника, работая вместе, могут выполнить всю работу за 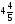 дня. Второй плотник, работая отдельно, мог бы выполнить эту работу на 4 дня быстрее, чем первый. За сколько дней каждый плотник, работая отдельно, мог бы выполнить эту работу? дня. Второй плотник, работая отдельно, мог бы выполнить эту работу на 4 дня быстрее, чем первый. За сколько дней каждый плотник, работая отдельно, мог бы выполнить эту работу?Решение Примем весь объем выполняемой работы за 1. Пусть первый плотник затратит на всю работу х дней, тогда второй – (х-4) дня. Значит производительность первого 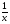 , второго – , второго – 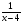 , поэтому , поэтому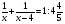 , т.е , т.е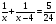 . .Решив полученное уравнение, получим х1=12; х2=3,6 Так как по условию задачи второй плотник мог бы выполнить работу на 4 дня быстрее, чем первый, то х2=3,6 не удовлетворяет смыслу задачи. Следовательно, первый плотник, работая один, мог бы выполнить всю работу за 12 дней, а второй – за 8 дней. Ответ: 12 дней; 8 дней. Для решения задач второго типа, текст задачи можно проиллюстрировать чертежами, что помогает учащимся зрительно видеть задачу. Пример 2. Новая машина может выкопать канаву за 8 часов, а старая – за 12. Новая работала 3 часа, а старая - 5 часов. Какую часть канавы осталось выкопать? Дадим наглядное представление этих задач. Условимся, что объем выполненной работы неизвестен, поэтому принимаем его за 1 и изображаем в виде отрезка, но отрезков будет три, так как возможны три случая: а. работает одна старая машина; б. работает одна новая машина; в. работают вместе обе машины. Выясним, почему отрезки равной длины (обе машины выполняют одну и ту же работу). н.м. 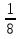 ст.м. 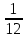 н.м. ст.м. ? 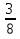 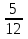 Разбор задачи. На сколько равных частей делим первый отрезок? На 8, так как работа выполняется за 8 часов. Что показывает 1 часть? Какую часть работы выполняет новая машина за 1 час, т.е. какова ее производительность? Так как новая машина работала 3 часа, то выполнила 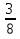 части все работы. Отмечаем на третьем отрезке - части все работы. Отмечаем на третьем отрезке - 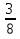 . .Аналогичные рассуждения проводим, рассматривая старую машину, и отмечаем на третьем отрезке - 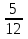 . .Далее рассматривается третий нижний отрезок, и по нему выясняется, как найти оставшуюся часть, т.е., отрезок, обозначенный знаком вопроса. 1 – ( 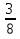 + + 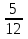 ) = ) = 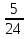 Ответ: осталось выполнить 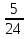 работы. работы.В связи с экономией времени деление отрезков производится «на глаз», хотя очень полезно показать, как можно разделить быстро на 4 равные части (отрезок делится пополам, а затем каждая часть еще пополам). Аналогично деление на 8 и т.д. На 6 частей – сначала пополам, а потом каждую часть - на три. Рассмотрим решение задач второго типа, используя формулу А = Р ∙ t Пример3, Маша и Настя вымоют окно за 20 минут, Настя и Лена – 15 минут, Маша и Лена – за 12 минут. За какое время девочки вымоют окно. Работая вместе? Решение А = Р ∙ t; р = А / t; t = А / Р Примем работу за единицу, тогда составим систему уравнений: М – р1 1/р1 + 1/р2 = 1/20 Н – р2 1/р2 + 1/р3 = 1/15 Л – р3 1/р1 + 1/р3 = 1/12 2(1/р1 + 1/р2 + 1/р3) =1/5 => (1/р1 + 1/р2 + 1/р3) =1/10 Ответ: 10 минут. 2.3 Задачи на концентрацию смесей и сплавов В задачах на концентрацию смесей и сплавов предполагается их однородность, и поэтому имеется прямо пропорциональная зависимость между объемами и массами рассматриваемых смесей и сплавов. Пусть смесь массой m содержит некоторое вещество массой М. Тогда концентрация данного вещества в смеси будет вычисляться по формуле 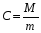 , ,а процентное содержание данного вещества равно 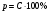 Задача1.(смеси) Смешали 30%-ный раствор соляной кислоты с 10%-ым и получили 600 г 15%-ого раствора. Сколько граммов каждого раствора было взято? Решение Пусть 30%-ого раствора взято х г, а 10%-ого – у г. Тогда из условия ясно, что х+у=600. В первом растворе 0,3х г кислоты, во втором – 0,1у г кислоты. Значит 0,3х+0,1у=0,15600. Составим систему и решим ее. 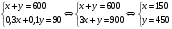 Ответ 150 г 30%-ого и 450 г 10%-ого раствора При решении текстовых задач нужно учить учащихся организовывать данные. Прекрасный способ — помещать данные в таблицу. Рассмотрим , как это делается, на следующем примере. Задача 2.(смеси) Сколько чистой воды нужно добавить к 100 граммам 60% раствора кислоты, чтобы получить 20% раствор? Разместим данные в следующей таблице:
Поскольку количество кислоты не меняется в процессе, мы можем написать уравнение 60 = 0,2 ∙ (100 + Х), решив которое, получим ответ: Х = 200 граммов. Чтобы решить данную задачу с помощью таблицы нужно сделать следующее:
Задача 3. (сплавы) имелось два сплава серебра. Процент содержания серебра в первом сплаве был на 25% выше, чем во втором. Когда сплавили их вместе, то получили сплав массой 40 кг, содержащий 30% серебра. Определите веса сплавов, если известно, что серебра в первом сплаве было 4 кг, а во втором 8 кг. Решение Составим таблицу
Т. к. 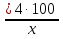 > > 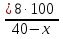 на 25%, то составим уравнение на 25%, то составим уравнение 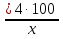 - - 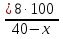 = 25% и решим его = 25% и решим егох1 = 8 х2 = 80 – не удовлетворяет условию задачи Ответ: вес 1 сплава - 8 кг, вес 2 сплава – 36 кг. 2.4 Задачи на проценты Процент – это сотая часть, наглядная иллюстрация процента может быть продемонстрирована на метровой школьной линейке с делениями по 1см. В данном случае 1 см является сотой частью линейки, т.е. 1%. Можно дать следующие задания: а. показать на линейке 25%, 40% и т.д. б. назвать число процентов, которые показываются на линейке. Затем работу можно продолжить на отрезках, задавая вопросы, например: Как показать 1% отрезка? Ответ: отрезок нужно разделить на 100 равных частей и взять одну часть. Условимся, что деление отрезка на 100 равных частей делаем условно. При решении задач на проценты следует объяснить учащимся, что прежде всего нужно выяснить, сколько составляет 1%. Рассмотрим сначала более простые задачи. Пример №1. Ученик прочитал 138 страниц, что составило 23% всех страниц книги. Сколько страниц в книге? Решение Число страниц в Кинге неизвестно, но число страниц составляет 100%. Так как 138 страниц составляют 23%, то находим, сколько приходится на 1%. 138 / 23 = 6 (стр.) – составляет 1%. Так как число страниц в книге составляет 100%, то 6 ∙ 100% = 600 (стр.) – в книге. Ответ: В книге 600 страниц. Пример №2. Мальчик истратил на покупку 40% имевшихся у него денег, а на оставшиеся 30 копеек купил билет в кино. Сколько денег было у мальчика? Решение Найдем, сколько процентов составляют 30 копеек. 100%-40% = 60% - составляют 30 копеек. Найдем, сколько составляет 1% 30 : 60 = 0,5 копеек 0,5 ∙ 100 = 50 копеек Ответ: 50 копеек Пример №3. В школе 700 учащихся. Среди них 357 мальчиков. Сколько процентов учащихся этой школы составляют девочки? Решение Число учащихся 700 человек, что составляет 100%. 700 / 100 = 7 (чел.) – составляют 1%. Узнаем, сколько процентов составляют мальчики. Для этого: 357 / 7 = 51% Узнаем, сколько процентов составляют девочки. 100%-51%=49% Ответ: 49% Рассмотрим более сложную задачу: Пример №4. Цена на товар сначала уменьшилась на 15%. А потом уменьшилась на 20%. На сколько процентов уменьшилась цена? Решение Пусть цена товара была - а. Стала: а ∙ (1 - 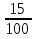 ) ∙ (1 - ) ∙ (1 - 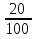 ) = а ∙ 0,85 ∙ 0, 8 = ) = а ∙ 0,85 ∙ 0, 8 = 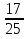 а = 0,68а а = 0,68аУменьшили: а – 0,68 = 0,32а 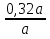 ∙ 100% = 32% ∙ 100% = 32%Ответ: 32% ЗАКЛЮЧЕНИЕ Из выше сказанного можно сделать вывод: задачи и решение их занимают в обучении школьников весьма существенное место и по времени, и по их влиянию на умственное развитие ребенка. 1. Текстовые задачи являются важным средством обучения математике. С их помощью учащиеся получают опыт работы с величинами, постигают взаимосвязи между ними, получают опыт применения математики к решению практических (или правдоподобных) задач. 2. Использование арифметических способов решения задач развивает смекалку и сообразительность, умение ставить вопросы, отвечать на них, то есть развивает естественный язык, готовит школьников к дальнейшему обучению. 3. Арифметические способы решения текстовых задач позволяют развивать умение анализировать задачные ситуации, строить план решения с учетом взаимосвязей между известными и неизвестными величинами (с учетом типа задачи), истолковывать результат каждого действия в рамках условия задачи, проверять правильность решения с помощью составления и решения обратной задачи, то есть формировать и развивать важные общеучебные умения. 4. Арифметические способы решения текстовых задач приучают детей к первым абстракциям, позволяют воспитывать логическую культуру, могут способствовать созданию благоприятного эмоционального фона обучения, развитию у школьников эстетического чувства применительно к решению задачи (красивое решение!) и изучению математики, вызывая интерес сначала к процессу поиска решения задачи, а потом и к изучаемому предмету. 5. Использование исторических задач и разнообразных старинных (арифметических) способов их решения не только обогащают опыт мыслительной деятельности учащихся, но и позволяют им осваивать важное культурно-историческое наследие человечества, связанный с поиском решения задач. Это важный внутренний (связанный с предметом), а не внешний (связанный с отметками, поощрениями и т.п.) стимул к поиску решений задач и изучению математики. Таким образом, использование алгоритмов, таблиц, рисунков, общих приемов дает возможность ликвидировать у большей части учащихся страх перед текстовой задачей, научить распознавать типы задач и правильно выбирать прием решения. Нередко, некоторые ученики просто списывают задачу с доски, не пытаясь вникнуть в ее смысл. Таким ученикам можно предложить творческую работы, где они должны сами составить задачу и решить ее. Составляя задачу, ученик более осознанно поймет существование зависимости между величинами, почувствует, что числа берутся не произвольно: некоторые задаются, а другие получаются на основе выбранных. При составлении задачи большое значение имеют и обратные задачи. Для активного участия в поиске решения хорошо использовать опорные карты-сигналы, которые должны быть у всех учащихся. СПИСОК ЛИТЕРАТУРЫ 1. Н.И. Попов, А.Н. Марасанов Задачи на составление уравнений. Учебное пособие. Йошкар-Ола: Мар. гос. ун-т, 2003г. 2. А. Тоом Как я учу решать текстовые задачи. - Еженедельная учебно-методическая газета «Математика», №46, 47, 2004г. 3. А. Прокофьев, Т. Соколова, В. Бардушкин, Т. Фадеичева Текстовые задачи. Материалы вступительных экзаменов в МИЭТ.–Еженедельная учебно-методическая газета «Математика», №9, 2005г. 4. Болтянский, В. Г. Как устроена теорема? [Текст] / В. Г. Болтянский // Математика в школе. – 1987. – № 1. – С. 41-49. 5. Обучение решению задач как средство развития учащихся: из опыта работы. Методическое пособие для учителя. – Киров, ИИУ. – 1999. – С.3-18. 6. Тоом А.Л. Между детством и математикой: Текстовые задачи в математическом образовании/ Математика, 2005, № 14 7. Фридман Л.М., Турецкий Е.Н. Как научится решать задачи: Кн для учащихся ст. классов сред. шк. – 3-е изд., дораб. – М.: Просвещение, 1989. – 192 с.: ил. 8. Шевкин А.В. Материалы курса «Текстовые задачи в школьном курсе математики»: Лекции 1-4. – М.: Педагогический университет «Первое сентября», 2006. 88 с. 9. Шевкин А.В. Материалы курса «Текстовые задачи в школьном курсе математики»: Лекции 5-8. – М.: Педагогический университет «Первое сентября», 2006. 80 с. 10. Методика преподавания математики [Текст]: учебник для вузов / Е.С.Канин, А. Я. Блох [и др.]; под ред. Р. С. Черкасова. – М.: Просвещение, 1985. – 268 с. 11. В. Булынин Применение графических методов при решении текстовых задач. – Еженедельная учебно-методическая газета «Математика», №14, 2005г. ТЕКСТОВЫЕ ЗАДАЧИ
11.Числитель обыкновенной дроби на 4 меньше знаменателя. Если числитель уменьшить, а знаменатель увеличить на 3, то полученная дробь будет вдвое меньше исходной. Найдите эту дробь. 12. Турист прошел 3 км по шоссе и 6 км по проселку, затратив на весь путь 2 часа. По шоссе он шел со скоростью на 2 км/ч большей, чем по проселку. С какой скоростью шел турист по проселку?
16. По окружности движутся два тела: первое тело проходит круг на 2 сек быстрее второго. Если тела движутся в одном направлении, то они встречаются через каждые 60 сек. Какую часть окружности проходит каждое тело за 1 сек? 17. Бак наполняется водой тремя трубами разного диаметра. Сначала в бак наливали через I трубу столько времени, сколько нужно для полного наполнения через II и III трубы вместе. Затем в бак наливали через II трубу столько времени, сколько нужно для полного наполнения через I и III трубы вместе. После чего пришел слесарь и вычислил, что через III трубу осталось наливать в бак до конца столько времени, сколько нужно для полного наполнения через I и II трубы вместе. Не ошибся ли он? 18. Два туриста вышли из A в B одновременно, причем первый турист каждый километр пути проходит на 5 мин быстрее второго. Первый, пройдя 1/5 часть пути, вернулся в A и, пробыв там 10 мин, снова пошел в B. При этом в B оба туриста пришли одновременно. Каково расстояние от A до B, если второй турист прошел его за 2,5 часов? 19. Пассажир, едущий из A в B, одну половину затраченного на путь времени ехал на автобусе, а вторую - на автомобиле. Если бы он ехал от A до B только на автобусе, то это заняло бы в полтора раза больше времени. Во сколько раз быстрее проходит путь от A до B машина, чем автобус? МОУ Новодмитриевская СОШ Работа на тему: Учитель математики: Калитвянская Нина Викторовна 2010 год    |
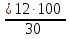 = 40
= 40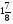 ч. За сколько часов вспашет поле один второй тракторист. Ответ: 5 ч.
ч. За сколько часов вспашет поле один второй тракторист. Ответ: 5 ч.