Содержание программы по математике в 9 классе
 Скачать 50.71 Kb. Скачать 50.71 Kb.
|
| Содержание программы по математике в 9 классе (6 часов в неделю, 204 часа – за год) I. Повторение материала 8 класса (7 часов ). Алгебраические дроби. Свойства квадратного корня. Квадратные и дробно – рациональные уравнения, решение задач с помощью уравнений. Функции: квадратичная, у=|x|, у= 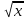 , у= , у=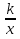 . Четырехугольники, площади фигур, подобие треугольников. . Четырехугольники, площади фигур, подобие треугольников.II. Рациональные неравенства и их системы (15 часов) Линейные и квадратные неравенства (повторение). Рациональные неравенства. Метод интервалов. Множества и операции над ними. Системы неравенств. Совокупности неравенств. Неравенства с модулями. Иррациональные неравенства. Задачи с параметрами. III. Векторы. Метод координат. (18 часов) Понятие вектора. Сложение и вычитание векторов. Умножение вектора на число. Координаты вектора. Простейшие задачи в координатах. Деление отрезка в данном отношении. Координаты середины отрезка. Уравнение окружности и прямой. Применение векторов и метода координат к решению задач. IV. Системы уравнений. (19 часов) Уравнения и неравенства с двумя переменными. Диофантовы уравнения. Основные понятия, связанные с системами уравнений и неравенств с двумя переменными. Рациональное уравнение с двумя переменными. Решение уравнения р(х;у)=0. Равносильные уравнения с двумя переменными. Формула расстояния между двумя точками координатной плоскости. График уравнения (х – а)2 + ( у – b)2 = r2. Методы решения систем уравнений (метод подстановки, алгебраического сложения, введения новых переменных). Равносильность систем уравнений. Однородные системы. Симметрические системы. Системы с модулями. Системы уравнений как математические модели реальных ситуаций. V. Числовые функции.(25 часов) Определение числовой функции. Независимая переменная. Зависимая переменная. Область определения функции. Естественная область определения функции. Область значений функции. Способы задания функции (аналитический, графический, табличный, словесный). Свойства функций (монотонность, ограниченность, выпуклость, наибольшее и наименьшее значения, непрерывность). Исследование функций: y=C, y=kx+m, y=kx2, y=|x|, у= 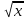 , у= , у=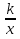 , y= ax2 +bx + c. , y= ax2 +bx + c.Четные и нечетные функции. Алгоритм исследования функции на четность. Графики четной и нечетной функций. Степенная функция с натуральным показателем, ее свойства и график. Степенная функция с отрицательным целым показателем, ее свойства и график. Функция 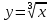 , ее свойства и график. , ее свойства и график.VI. Соотношения между сторонами и углами треугольника. Скалярное произведение векторов. (11 часов) Синус, косинус, тангенс угла 00, 300, 450,600, 900,1800. Основное тригонометрическое тождество. Формулы вычисления координат точки. Соотношения между сторонами и углами треугольника. Теорема о площади треугольника. Теоремы синусов и косинусов. Формула вычисления радиуса описанной окружности. Скалярное произведение векторов, его свойства. Решение треугольников. VII. Прогрессии. (17 часов) Числовая последовательность. Способы задания числовых последовательностей (аналитический, словесный, рекуррентный). Свойства числовых последовательностей. Арифметическая прогрессия. Формула n – го члена. Формула суммы членов конечной арифметической прогрессии. Характеристическое свойство. Геометрическая прогрессия. Формула n – го члена. Формула суммы членов конечной геометрической прогрессии. Характеристическое свойство. Прогрессии и банковские расчеты. Метод математической индукции. VIII. Длина окружности. Площадь круга.(12 часов) Правильные многоугольники. Определение и его свойства. Формулы вычисления углов, площади, стороны правильного многоугольника и радиуса вписанного в него и описанного около него окружности. Длина окружности, длина дуги окружности. Площадь круга, площадь кругового сектора. IX. Элементы комбинаторики, статистики и теории вероятностей. (13 часов) Комбинаторные задачи. Правило умножения. Факториал. Перестановки. Основные понятия математической статистики. Группировка информации. Общий ряд данных. Кратность варианты измерения. Табличное представление информации. Частота варианты. Графическое представление информации. Полигон распределения данных. Гистограмма. Числовые характеристики данных измерения (размах, мода, среднее значение). Вероятность. Событие (случайное, достоверное, невозможное). Классическая вероятностная схема. Противоположные события. Несовместные события. Вероятность суммы двух событий. Вероятность противоположного события. Статистическая устойчивость. Статистическая вероятность. X. Движения. (8 часов) Понятие движения, отображение плоскости на себя. Параллельный перенос и поворот. Центральная и осевая симметрия. Композиция движений. Применение движения к решению задач. XI. Тригонометрические выражения и их преобразования.(20 часов) Тригонометрические функции любого угла. Определение тригонометрических функций. Знаки тригонометрических функций. Значения тригонометрических функций углов 00, 300, 450,600, 900,1800, 2700, 3600 . Единичная окружность. Радианная мера угла. Основные тригонометрические формулы: основное тригонометрическое тождество, формулы зависимости тригонометрических функций одного и того же угла, формулы сложения, формулы суммы, формулы двойного угла. Формулы приведения. Преобразование тригонометрических выражений. XII. Начальные сведения стереометрии. (8 часов) Аксиомы стереометрии. Понятие многогранника. Элементы многогранников. Призма. Пирамида. Тела вращения. Понятие конической и цилиндрической поверхностей. Понятие сферы и шара. XIV. Повторение. Решение задач. (31 час) Числовые выражения. Алгебраические выражения. Функции и графики. Уравнения и системы уравнений. Неравенства и системы неравенств. Задачи на составление уравнений или систем уравнений. Арифметическая и геометрическая прогрессии. Применение векторов и метода координат к решению задач. Решение треугольников. Формулы вычисления углов, площади, стороны правильного многоугольника и радиуса вписанного в него и описанного около него окружности. |