Решение задач на смеси и сплавы с помощью расчетной формулы
 Скачать 76.07 Kb.
|
| Разработка учебного занятия по подготовке к ЕГЭ (профильный уровень) Плюснина Евгения Кирилловна, учитель математики, МКОУ «Ключинская СШ», Ачинского района. ([email protected]). Тема: Решение задач на смеси и сплавы с помощью расчетной формулы Предметная область – математика Участники - учащиеся 11 класса МКОУ «Ключинская СШ» - 6 человек. Цели и задачи: Образовательные – познакомить учащихся с методами решения задач на сплавы и смеси; Применять расчетную формулу при решении задач, использовать межпредметные связи. Развивающие – развивать творческую и мыслительную деятельность учащихся, интеллектуальные качества личности, такие как самостоятельность, способность к оценочным действиям, обобщению, быстрому переключению; способствовать формированию навыков самостоятельной работы; формировать умение четко и ясно излагать свои мысли. Воспитательные – прививать учащимся интерес к предмету; формировать умение аккуратно и грамотно выполнять математические записи. Образовательный результат - на ЕГЭ решать и решить задачу на смеси и сплавы В результате работы учащиеся должны знать:
Уметь: Уметь строить и исследовать простейшие математические модели
Аннотация. В числе текстовых задач особое место занимают задачи на смеси, растворы и сплавы. Задачи эти включены в кодификаторы ЕГЭ и по химии, и по математике, причем в структуре экзаменационной работы считаются заданиями повышенного уровня сложности. На решение задач на смеси и сплавы я отвожу 3 часа (в 11 классе), причем один час –лекция, где я рассказываю некоторые теоретические сведения, методы решения задач, показываю на примере одной задачи применение нескольких методов. В конце лекции выяснила какой метод показался проще и этим методом будут решать задачи на экзамене, объяснить почему понравился. Из 6 учеников 4 выбрали метод с помощью расчетной формулы 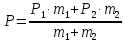 объясняя, что формула проста в применении, не требует перевода чисел в десятичные дроби, т.е. работа с натуральными числами и за счет этого можно сэкономить время на экзамене для выполнения других заданий. Ученики получили задание на дом найти из вариантов ЕГЭ задачи на смеси и сплавы, условие задачи записать на карточку, а решение задачи в тетрадь. Задачи можно взять из Открытого банка заданий, обучающего сайта «Решу ЕГЭ» Д. Гущина, тренировочных вариантов А. Ларина., книги ЕГЭ 2015 Математика Типовые тестовые задания под редакцией И.В. Ященко и другие, но обязательно указать источник.Я решила провести учебное занятие –консультацию с применением ИКТ. Занятие рассчитано на 90 минут. План занятия: 1. Организационный момент (2 мин) 2. Объявление темы занятия (2мин) 3. Работа над темой 1) проверка домашнего задания (15 мин) 2) работа на компьютерах, с текстами (26 минут) - выбор задач - классификация - решение задач 4. Взаимообмен заданиями(10мин) 5. Творческое задание. (10 мин) 6.Проверка усвоения материала - выполнение теста (22 мин)
Ход занятия
« Решение задач на смеси и сплавы с помощью расчетной формулы». В результате нашей работы мы должны знать:
Уметь:
Работа над темой :
В числе текстовых задач особое место занимают задачи на смеси, растворы и сплавы, называемые еще задачами на процентное содержание или концентрацию. Концентрацией называется величина, равная отношению массы (объема) вещества, входящего в смесь к массе (объему) смеси. Это отношение может быть выражено либо в дробях, либо в процентах (например 20%, или 0,2). При решении задач о смесях, сплавах, растворах используют следующие допущения: 1) все полученные смеси, сплавы, растворы считаются однородными; 2) не делается различия между литром как мерой вместимости сосуда и литром как мерой количества жидкости (или газа); 3) смешивание различных растворов происходит мгновенно; 4) объем смеси равен сумме объемов смешиваемых растворов; 5) объемы растворов и массы сплавов не могут быть отрицательными. 2.Методы решения задач. Основными методами решения задач на смешивание растворов являются:
Задачи на смеси (сплавы) можно разделить на два вида: 1.Задаются, например, две смеси (сплава) с массами m1 и m2 и с концентрациями в них некоторого вещества. Смеси (сплавы) сливают (сплавляют). Требуется определить массу этого вещества в новой смеси (сплаве) и его новую концентрацию. 2.Задается некоторый объем смеси (сплава) и от этого объема начинают отливать (убирать) определенное количество смеси (сплава), а затем доливать (добавлять) такое же или другое количество смеси (сплава) с такой же концентрацией данного вещества или с другой концентрацией. Эта операция проводится несколько раз. Решение задач. Запишите формулу 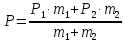, где P – процентное содержание вещества m- масса вещества, запомните, процентное содержание воды равно нулю. 1.Зная эту формулу вы можете оказать помощь маме при заготовках на зиму. Очень часто в рецептах используют 6% уксусную кислоту, а у мамы только 70% уксусная кислота. Сколько граммов надо взять 70% уксусной кислоты, чтобы получить 200 граммов 6%. Решение. Пусть х граммов 70% уксусной кислоты, P=6, P1=70 P2(вода)=0, m1-х m2=200г 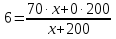 6х+1200=70х 64х=1200 х=18,75 Ответ: 18,75 граммов 70% уксусной кислоты(примерно одна чайная ложка. 2.  (слайд 14-17) Некоторые важные утверждения принимают без доказательства, их называют аксиомами или бесспорными истинами. Первая такая истина заключается в следующем: Через любые две точки можно провести прямую и только одну. 13 Уметь строить и исследовать простейшие математические модели   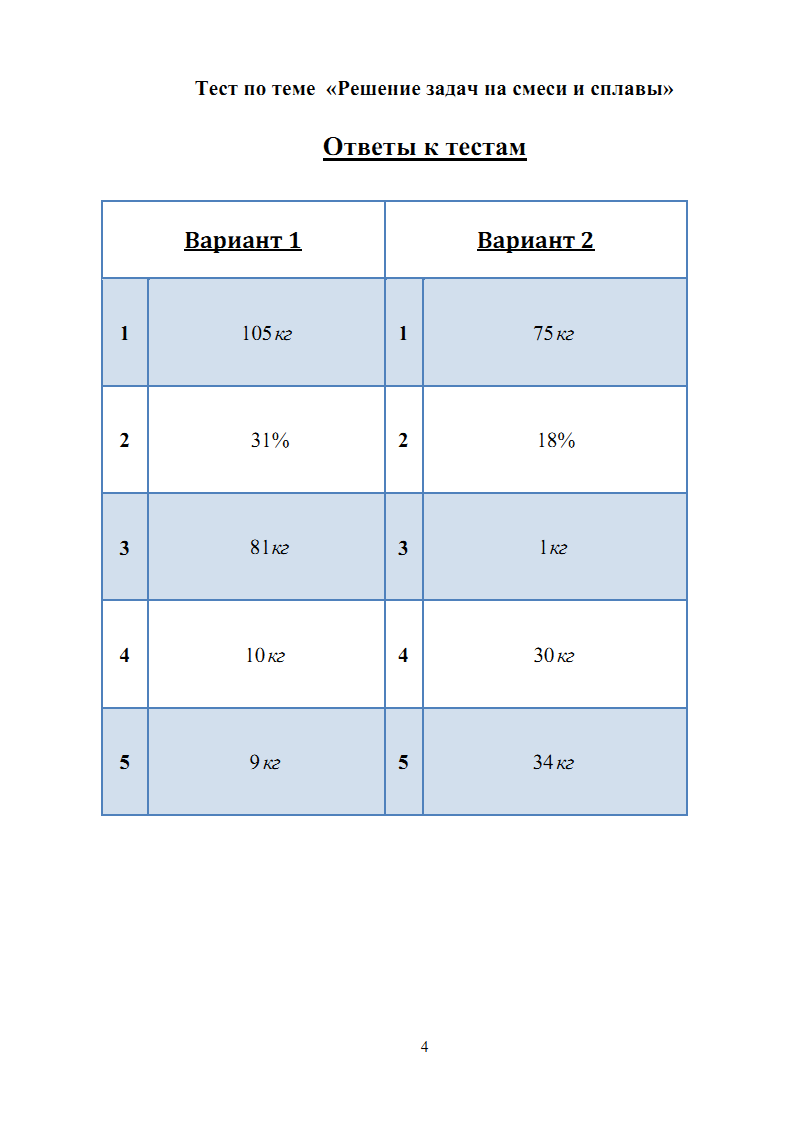 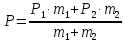|