«Решение стереометрических задач при подготовке к егэ»

V Всероссийский сетевой конкурс «Профессиональный успех–XXI»

• Направленность: Презентация в образовательном процессе

• Наименование номинации 6.1: Презентация в работе с детьми

• Название работы: «Решение стереометрических задач при

• подготовке к ЕГЭ»

• Автор: Груздева Татьяна Александровна,

• учитель математики МБОУ Тонкинской СОШ,

• Нижегородская область

• 2015 год

Данная презентация используется на факультативных и элективных занятиях при подготовке выпускников к сдаче ЕГЭ

• Данная презентация используется на факультативных и элективных занятиях при подготовке выпускников к сдаче ЕГЭ

• Цель: Повторить и обобщить материал по теме «Решение стереометрических задач при подготовке к ЕГЭ» и применить полученные знания в практической деятельности при решении задач.

• Задачи:

• Учебная: Закрепить знания и умение решать стереометрические задачи; применять ранее приобретенные знания к решению геометрических задач.

• Развивающая: Развивать математическую логику, креативное мышление, пространственное воображение, навыки самостоятельной и творческой деятельности.

• Воспитательная: Воспитывать интерес к предмету, точность и аккуратность в построении чертежа к геометрической задаче.

• Презентация отражает следующие вопросы геометрии:

• Расстояние от точки до прямой;

• Расстояние от точки до плоскости;

• Расстояние между двумя прямыми.

Расстояние от точки до прямой – это длина перпендикуляра, проведённого из данной точки к данной прямой.

• Расстояние от точки до прямой – это длина перпендикуляра, проведённого из данной точки к данной прямой.

Дано: АВСДА1В1С1Д1 – куб. АВ = 1. Найти: Расстояние от точки С до прямой ВД1.

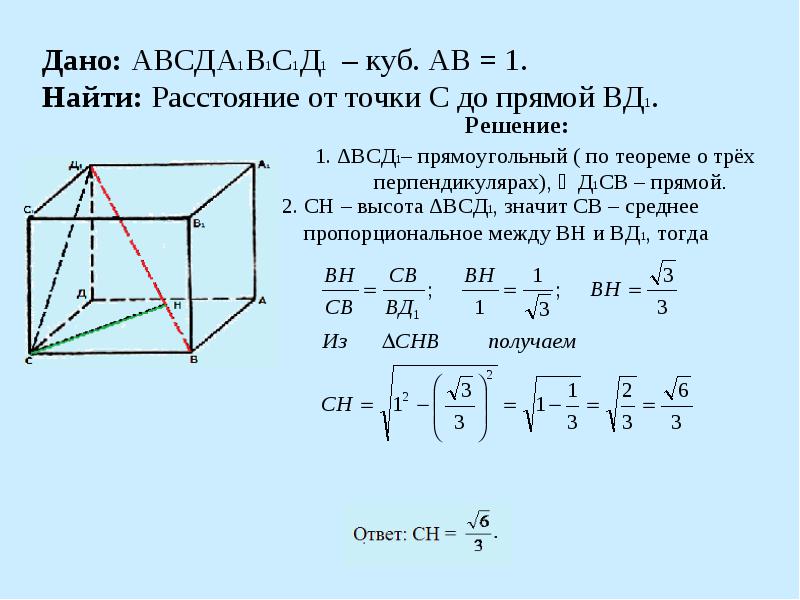
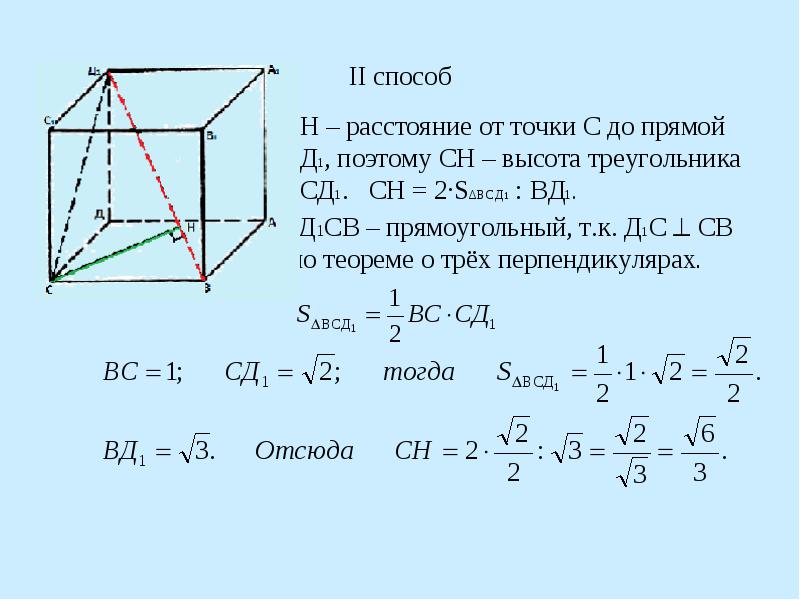
II способ

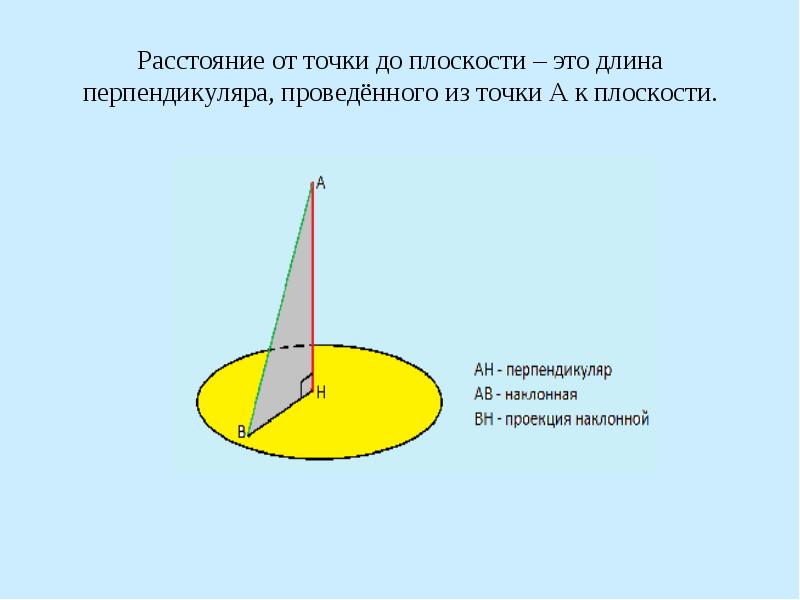
Расстояние от точки до плоскости – это длина перпендикуляра, проведённого из точки А к плоскости.

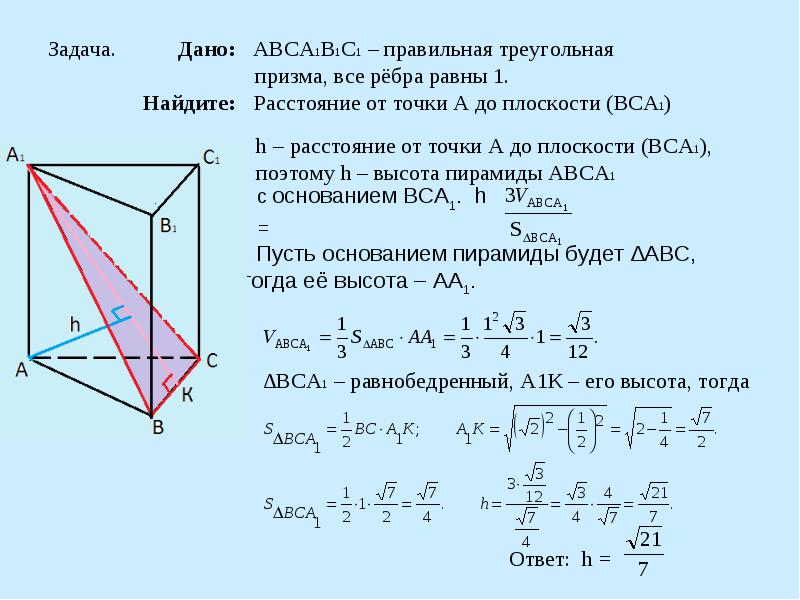
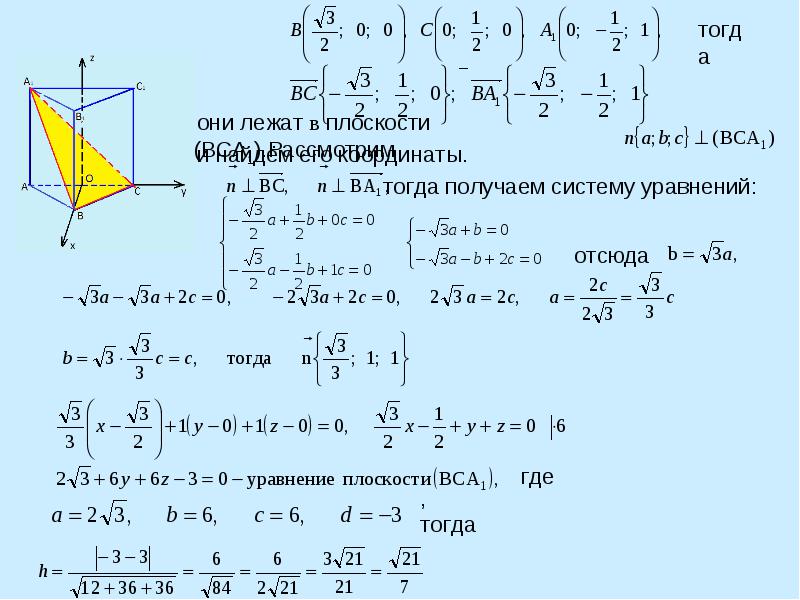
Задача. Дано: АВСА1В1С1 – правильная треугольная призма, все рёбра равны 1. Найдите: Расстояние от точки А до плоскости (ВСА1)

За страницами учебника Расстояние от точки А до плоскости можно вычислить по формуле:

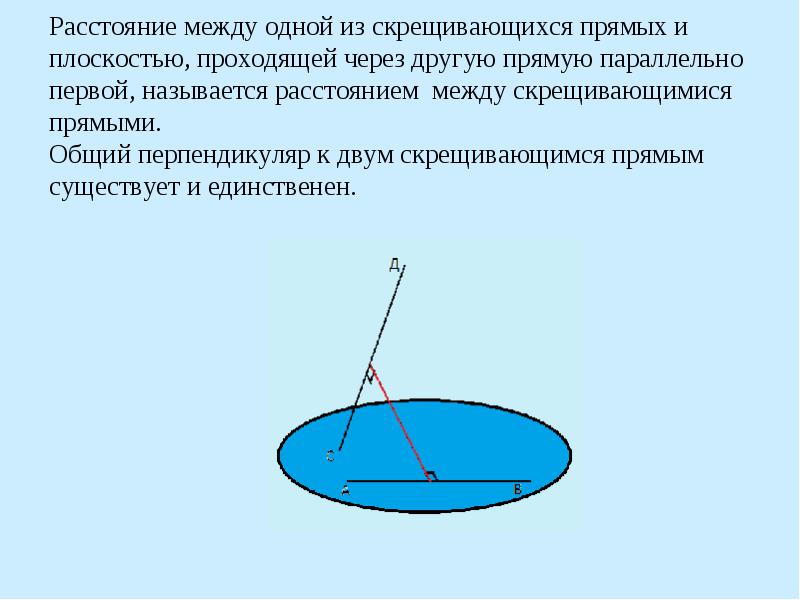
Расстояние между одной из скрещивающихся прямых и плоскостью, проходящей через другую прямую параллельно первой, называется расстоянием между скрещивающимися прямыми. Общий перпендикуляр к двум скрещивающимся прямым существует и единственен.

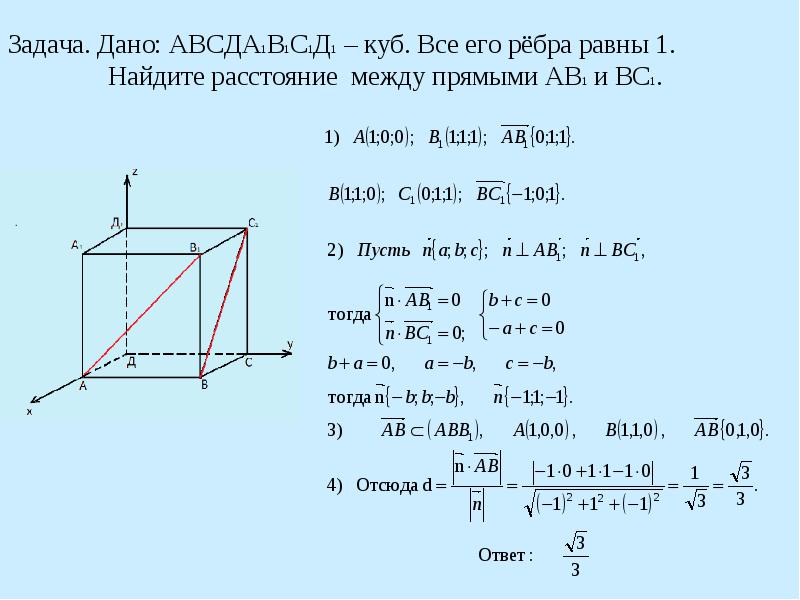
Задача. Дано: АВСДА1В1С1Д1 – куб. Все его рёбра равны 1. Найдите расстояние между прямыми АВ1 и ВС1.

За страницами учебника

• Расстояние между скрещивающимися прямыми можно найти по формуле:

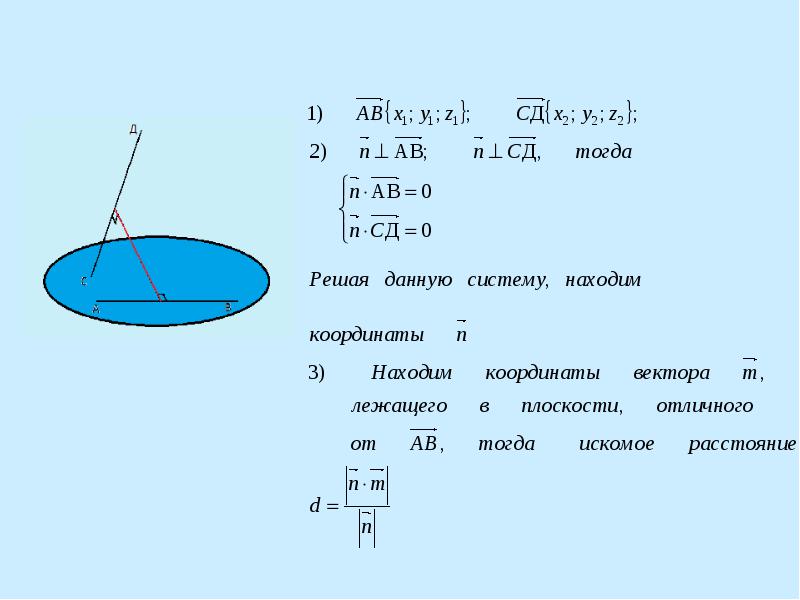
Задача. Дано: АВСДА1В1С1Д1 – куб. Все его рёбра равны 1. Найдите расстояние между прямыми АВ1 и ВС1.

Задача 2. Дано: SABCD – правильная четырёхугольная пирамида, все рёбра которой равны 1. Найдите: Расстояние между прямыми АS и ВС.

Литература:

• Геометрия 10 – 11 классы. Учебник для общеобразовательных учреждений. Базовый и профильный уровни. Авторы: Л.С. Атанасян, В.Ф.Бутузов, С.Б.Кадомцев, Л.С.Киселева, Э.Г.Позняк Москва «Просвещение» 2013 год

• Избранные вопросы профильного и предпрофильного курса математики. Авторы: И.Г.Малышев, М.А. Минчасова, Б.Н.Иванов. Нижний Новгород Нижегородский гуманитарный центр, 2007 год

• ЕГЭ 2011 Математика Задача С2 Геометрия Стереометрия Под редакцией А.Л.Семенова и И.В.Ященко Москва Издательство МЦНМО 2011