«Разложение квадратного трёхчлена на множители»
 Скачать 52.08 Kb. Скачать 52.08 Kb.
|
| Кичигина Надия Хамзеевна МБОУ СОШ №16 Тема урока: «Разложение квадратного трёхчлена на множители» (алгебра 8 класс) Цель: восприятие и первичное осознание нового материала; изучить основные понятия, связанные с квадратным трёхчленом; вывести формулу для разложения квадратного трёхчлена на множители и формировать умение её применять. Тип урока: изучение и первичное закрепление новых знаний; Структура урока: мотивация- актуализация опорных знаний -восприятие, осмысление, закрепление-проверка усвоения - анализ и самоанализ. Ход урока. 1.Организационный момент. 2.Актуализация знаний. Сегодня мы продолжим работу с квадратным уравнением, используя теорему Виета и применением квадратного уравнения для новых алгебраических преобразований. Работа у доски по карточкам.( 2 ученика) Карточка №1:Составить квадратное уравнение, имеющее корни 3 и 2 ,через составление произведения. Карточка №2: Составить квадратное уравнение, имеющее корни 3 и 4 ,используя формулу Виета. Остальные устно: (слайд №1) Сократить дробь: 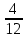 ; ; 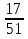 ; ; 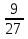 ; ; 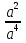 ; ; 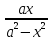 ; ; 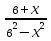 ; ;№2 Назовите коэффициенты квадратного уравнения: а) 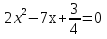 б) - 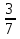 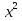 - - 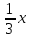 + 5 = 0 + 5 = 0(слайд 2) в) 2х2- 7х + 3 = 0 – преобразуйте в приведённое квадратное уравнение (один человек к доске записать полученное приведённое квадратное уравнение) -Назовите коэффициенты полученного уравнения. (р= - 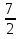 ; или - ; или - 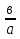 ; g = ; g =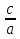 ) )-Проверяем работу учеников, работающих по карточкам: №1 (х-3)(х-2) = 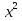 - 5х +6 ; №2 - 5х +6 ; №2 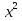 - 7х + 12 = 0 т. к. 3 + 4 = 7 , 3*4 = 12 - 7х + 12 = 0 т. к. 3 + 4 = 7 , 3*4 = 123. Объяснение нового материала: -Назовите общий вид квадратного уравнения ( 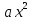 + + 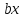 + с = 0 ) + с = 0 )Я вытру ноль. 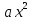 + + 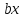 + с, где + с, где 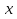 - переменная, а, - переменная, а, 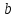 и с- некоторые числа, причём и с- некоторые числа, причём 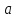 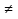 0 0-Как вы назовёте это выражение?(возможен ответ: многочлен второй степени с одной переменной) -Это квадратный трёхчлен. Сегодня нам предстоит познакомиться с новой темой: «Разложение квадратного трёхчлена на множители» (Запишем в тетради число, классная работа и тема урока) -Дайте определение квадратного трёхчлена.(слайд 3) Квадратным трёхчленом называется многочлен вида 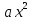 + + 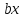 + с, где + с, где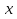 - переменная, а, - переменная, а, 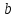 и с- некоторые числа, причем, а и с- некоторые числа, причем, а 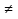 0 0 (слайд 4) Задание: Определите, какие из следующих выражений являются квадратным трёхчленом; ответ объясните. а) 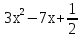 б) б) 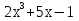 в) в) 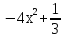 г) 2х – 1,27 д) 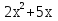 Заметим, что значение квадратного трёхчлена 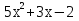 зависит от значения х.Например, зависит от значения х.Например,Если х = 0,то 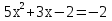 Если х = 2,то 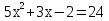 Если х = -1,то 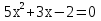 При х = -1 квадратный трёхчлен 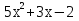 обращается в нуль,в этом случае число -1 называют корнем квадратного трёхчлена. обращается в нуль,в этом случае число -1 называют корнем квадратного трёхчлена.-Сформулируйте определение корня квадратного трёхчлена.(слайд 5) Определение. Корнем квадратного трёхчлена называется значение переменной, при котором значение этого трёхчлена равно нулю. -Как отыскать корни квадратного трёхчлена? Приравнять к нулю трёхчлен и найти дискриминант. -Итак, появилось новое понятие дискриминант квадратного трёхчлена Определение. Дискриминантом квадратного трёхчлена 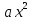 + + 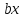 + с называется значение выражения D = b2 – 4 + с называется значение выражения D = b2 – 4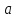 с . с .Если D 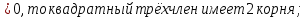 Если D 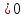 , то квадратный трёхчлен имеет 1 корень или 2 равных корня; , то квадратный трёхчлен имеет 1 корень или 2 равных корня;Если D 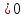 , то квадратный трёхчлен не имеет корней. , то квадратный трёхчлен не имеет корней. Вы умеете составлять квадратное уравнение, если известны корни, а квадратный трёхчлен - это его левая часть. Нам предстоит выполнить обратную работу. Посмотрите на работу ученика, работающего по карточке №1: (х-3)(х-2) = 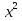 - 5 - 5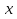 +6 +6Поменяем местами левую и правую части этого равенства 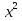 - 5х +6 = (х-3)(х-2) - 5х +6 = (х-3)(х-2)Вывод: получилось, что трёхчлен разложен на множители, а 2 и 3 это корни квадратного трёхчлена. -Рассмотрим другой трёхчлен 2 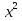 - 10х + 12 . Как его разложить на множители? - 10х + 12 . Как его разложить на множители?2 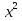 - 10х + 12 = 2( - 10х + 12 = 2(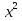 - 5х +6) = 2(х-3)(х-2) , где а = 2 – первый коэффициент. - 5х +6) = 2(х-3)(х-2) , где а = 2 – первый коэффициент.Запишем в общем виде: 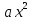 + + 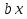 + с = + с = 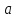 (х - (х - 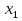 )(х - )(х - 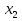 ) , где ) , где 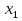 и и 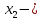 корни квадратного трёхчлена корни квадратного трёхчлена 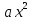 + + 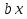 + с . + с .-Мы получили разложение квадратного трёхчлена на множители. Откроем страницу 136 учебника. Читаем вслух правило в рамочке.(слайд 6) Если 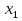 и и 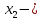 корни квадратного трёхчлена корни квадратного трёхчлена 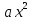 + + 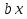 + с, + с, то 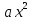 + + 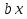 + с = + с = 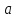 (х - (х - 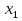 )(х - )(х - 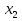 ) )Наш вывод совпал с выводом учебника. Это можно доказать перемножив множители правой части. В учебнике есть доказательство. Кто желает рассмотреть доказательство дома и на следующем уроке показать его нам?(слайд 7) Итак, если квадратный трёхчлен имеет корни, то он раскладывается на множители. Читаем обратное утверждение: Если квадратный трёхчлен раскладывается на линейные множители, то он имеет корни. По - другому, читаем в книге стр.137 в рамке Если квадратный трёхчлен не имеет корней, то его нельзя разложить на линейные множители. 4 .Формирование умений и навыков: Мы с вами будем формировать умения в разложении квадратного трёхчлена на множители. №531(а,в)-показывает учитель. а) 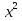 - 15х + 50 = (х-5)(х-10) - 15х + 50 = (х-5)(х-10)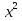 - 15х + 50 = 0 - 15х + 50 = 0Д 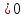 , , 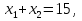 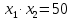 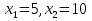 в) 3 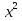 - 2х – 1 = 3(х - - 2х – 1 = 3(х - 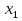 )(х - )(х - 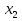 ) , не приведённое ,тогда а = 3 и 3 ) , не приведённое ,тогда а = 3 и 3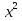 - 2х – 1 = 0, Д - 2х – 1 = 0, Д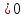 ,Д = 4 +12 =16, ,Д = 4 +12 =16, 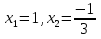 №532(б,г) устно(Чтобы разложить на множители нужно знать корни.)№533(а,г ), №538(а) 5.Проверочная самостоятельная работа на листах.(слайд 8) 1в. №533(б),№535(а),№538(в) 2в. №533(в),№535(б),№538(б) Оценочная таблица.
6. Итог. -Когда можно, а когда нельзя разложить на множители квадратный трёхчлен? Оценки: 2 ученика по работе с карточками, остальные по итогам проверочной работы. 7. Домашнее задание. П.3.7,№531(б,г), №533(д,е) , №538(г) (слайд 9) Спасибо за урок, дети. (слайд 10) Хабаровск, 2014 |